この節では,ポールが2個存在するアンプに負帰還をかけることを想定し,
さまざまな位相補償の方法と,その定数の定め方を見ていきます.
モデルとするアンプは,低域のゲインが A0 = 100 で,
2つのポールのカットオフ周波数を 20kHz と 100kHz と仮定します.
このアンプに帰還率 ![]() = 0.1 の負帰還をかけます.
低域のループゲインは
T0 = A0
= 0.1 の負帰還をかけます.
低域のループゲインは
T0 = A0![]() = 100 x 0.1 = 10,
帰還量は F = 1 + T = 11 で,20.8dB です.
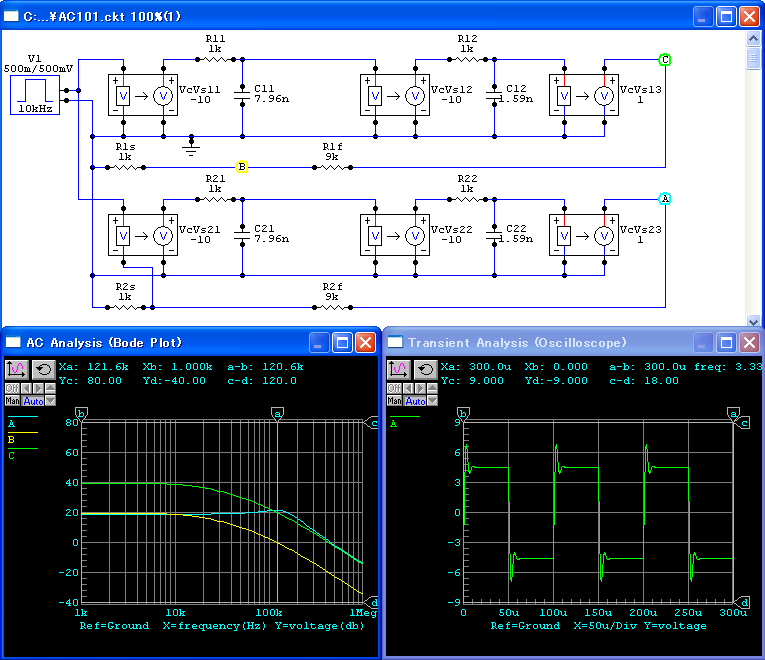
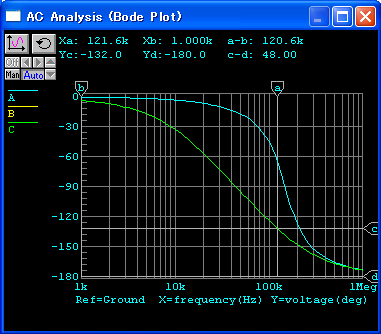
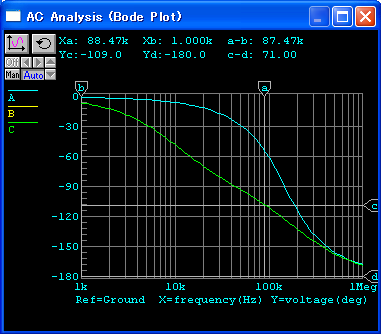
オープンループゲイン,ループゲイン,クローズドループゲインのボーデ線図を
図111に示します.
ゲイン交点周波数は,124kHz で,そのときの位相は
-132o,
位相余裕は 48o で,帰還後の特性にピークが生じています.
帰還後の -3 dB 点は,203kHz です.
= 100 x 0.1 = 10,
帰還量は F = 1 + T = 11 で,20.8dB です.
オープンループゲイン,ループゲイン,クローズドループゲインのボーデ線図を
図111に示します.
ゲイン交点周波数は,124kHz で,そのときの位相は
-132o,
位相余裕は 48o で,帰還後の特性にピークが生じています.
帰還後の -3 dB 点は,203kHz です.
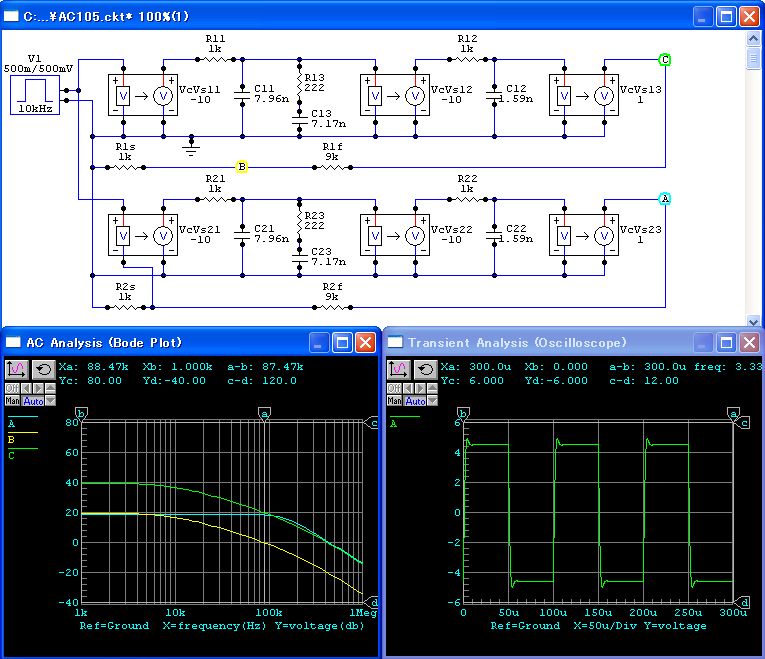
SPICEでシミュレーションするには,図112のようにします. ゲイン段は,後でMiller効果を用いた補正を行うため, 10倍の反転増幅を2段重ねています. 2つのポールは,RCによるローパス回路で実現します. 最後にゲインが1のバッファにより,RC回路の影響を遮断して出力としています.
ループゲインは,入力を与えずに,負帰還ループを開いてそのゲインを測るべきですが, このシミュレーションの回路の形式では,入力から
負帰還の節で調べたように,
周波数特性でピークを生じないようにするには,
Q = 0.707 とする必要があります.
このとき必要なスタガ比は,
![]() = 2T0 = 20 です.
現在のスタガ比は
= 2T0 = 20 です.
現在のスタガ比は
![]() = p2/p1 = 5 です.
= p2/p1 = 5 です.
スタガ比を大きくするには,
狭帯域化およびラグリード補償は,第一ポール p1 を生じている箇所で行います.
微分型補償は,負帰還回路(![]() 回路)で行うため,
一般に p1 とも p2 とも干渉せずに定数を決めることができます.
狭帯域化と同様な周波数特性を得るために,p1 以外の箇所で補償をすることもでき,ステップ補償と呼ばれます.
回路)で行うため,
一般に p1 とも p2 とも干渉せずに定数を決めることができます.
狭帯域化と同様な周波数特性を得るために,p1 以外の箇所で補償をすることもでき,ステップ補償と呼ばれます.
狭帯域化では,第一ポールをさらに下げて必要なスタガ比を確保します.
![]() = 20 とするためには,移動後の第一ポール p1' を,
= 20 とするためには,移動後の第一ポール p1' を,
p1' = 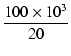 = 5 [kHz] = 5 [kHz]
|
(336) |
|
Cf = |
(337) |
狭帯域化による補償を行った場合,図115のように, ゲイン交点周波数は,45.3kHz になり,そのときの位相は -108o, 位相余裕は 72o になります. 帰還後の -3 dB 点は,74kHz です.
補償後のシミュレーションは,図116のようになります.
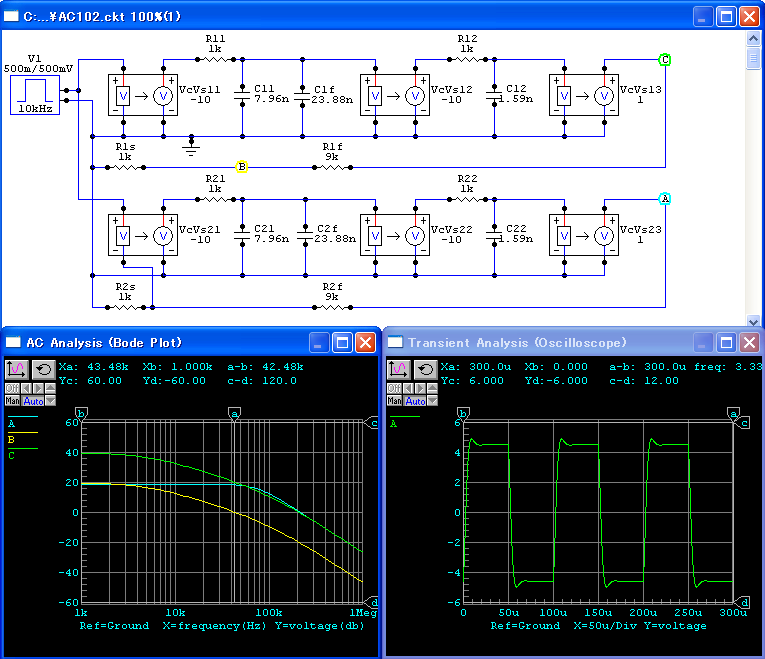
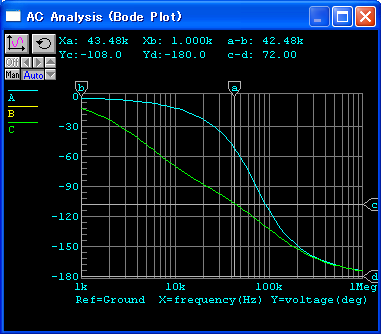
補償後の特性にピークは見られなくなり, オーバーシュートは4.2%程度で, ほぼ2次のバタワース特性といえます.
第一のポールを生じている部分のインピーダンスが低く,補償容量が大きくなる場合は, 直後のゲイン段にコンデンサを入れれば, ミラー効果により増幅度の分大きなコンデンサの働きをしますから, 小さな容量で同等な効果を得ることができます. たとえば,直後のゲインが10倍であれば, コンデンサの容量を1/(1+10)にできます.
ミラー効果を利用した狭帯域化のシミュレーションを図118に示します.
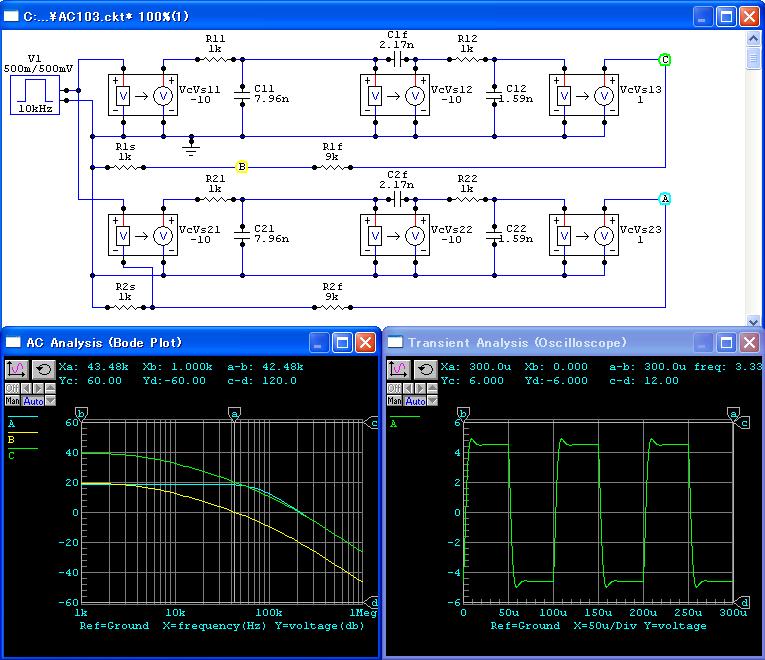
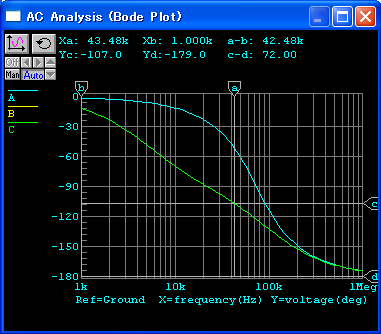
図116の補償容量の1/11を使用していますが, 同等の効果が得られています.
実際には,この例の回路では,補償容量はR11の右端とR12の右端の間に入ります. 8.8節で見たように,こうすると p2 は極分離によってさらに高い周波数へと移動するので,負帰還はさらに安定にかかるようになります.
狭帯域化を行いたくても,第一ポールの容量を増やせない場合は, 図120の(b)のようなステップ特性を挿入することにより, 同図(c)のようにポールの位置を下げることができます.
ステップ補償の回路は,図121のようなものです.
この回路の伝達特性は,
A(s) =  . . 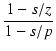
|
(338) |
| p | = | - 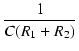 |
(339) |
| z | = | - |
(340) |
| CR2 | = | - |
(341) |
| R1 | = | (342) |
ステップ補償による狭帯域化のシミュレーションを,図122に示します.
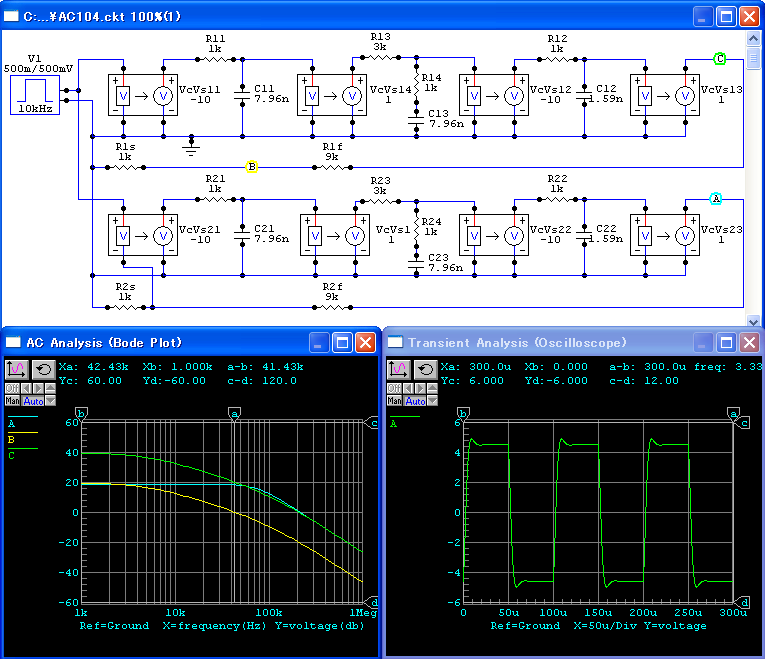
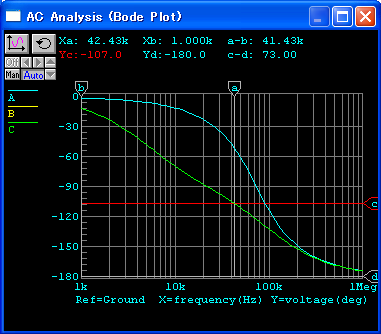
このモデルアンプの場合,第一ポールを構成している時定数は, 1 x 103 Ω, 7.96 x 10-9 F なので, この値をそのまま補償回路の R2 と C として使いました. R1 は,
|
R1 = |
(343) |
今回は,バッファ VcVs14 を追加して,p1, p2 に影響のないようにしています.
実際には,位相補償のために周波数特性が無限にのびたバッファを入れることはありえません.
通常は,p2 を生じている段にステップ補償を行うことになります.
シミュレーションの回路の場合,
図121の R1 が
1 kΩ と定められていますので,
| R2 | = | R1/3 = 333 Ω | |
| C | = | 7.96 x 10-9 . 3 = 23.88 x 10-9 F |
第一ポール p1 がある部分の特性を,図124の左上から右上のように変更できれば,全体の特性を右下のようにすることができ, 必要なスタガ比を得ることができます. すなわち,もともとあったポール p1 を p1' に移動し, p2 にゼロを作り,p2' に新たにポールを作ります.
このような特性を得るには,図125のように, 抵抗とコンデンサを直列にしたものを,第一ポールを生じている部分に入れます.
p1 を p1' へと低くする比率と,
p2 を p2' へと高くする比率は等しく,
これを ![]() (極の分離係数)とします.
つまり,
(極の分離係数)とします.
つまり,
|
|
(344) |
|
|
(345) |
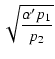
|
(346) |
この ![]() を用いて p1 以外の極(p2 はゼロですが)を p1 を使って表すと,
を用いて p1 以外の極(p2 はゼロですが)を p1 を使って表すと,
この希望する周波数特性を持つ伝達関数は,
A(s) = 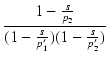
|
(350) |
一方,図125の回路の伝達関数は,
A'(s) = - gmR1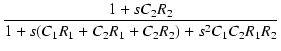
|
(352) |
|
C1R1 = - |
(356) |
- 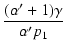 |
= | C1R1 + 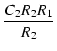 + C2R2 + C2R2 |
|
| = | C1R1 + |
||
| = | - 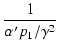 |
||
| ( |
= | ||
| = | |||
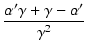 |
= | ||
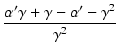 |
= | ||
| R2 | = | 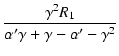 |
|
| = | 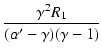 |
(357) |
|
C2 = - |
(358) |
モデルアンプの場合の定数を求めます.
極の移動係数 ![]() は,
は,
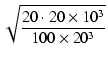 = 2 = 2
|
(359) |
| R2 | = | 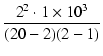 = 222 [Ω] = 222 [Ω] |
(360) |
| C2 | = | 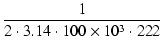 = 7.17 x 10-9 [F] = 7.17 x 10-9 [F] |
(361) |
ラグリード補償を行った場合,図126のように, ゲイン交点周波数は,90.5kHz になり,そのときの位相は -108o, 位相余裕は 72o になります. 帰還後の -3 dB 点は,148kHz です.
ラグリード補償による狭帯域化のシミュレーションを,図127に示します.
簡単に定数の目安をつけるには,次のようにします. p1' は,C1 と C2 の並列合成値と R1 によって概ね決まります. 今回の場合,p1' を p1 の半分にしたいので, C2 としては C1 と同じ値を使えばよいことがわかります.
p2' は,R2 と C2 によって決まります. 今回の場合,これが p2 の2倍となるように,R2 の値を決めます.
微分型補償は,図129のように, 帰還抵抗 Rf に補償用のコンデンサ Cf を並列に接続し, 第二のポール p2 をさらに高域に移動させるものです.
この ![]() 回路の伝達特性は,
回路の伝達特性は,
| zf | = | - |
(363) |
| pf | = | - 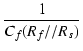 |
(364) |
![]() 回路のポールとゼロの比率は,
回路のポールとゼロの比率は,
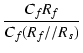 =
= 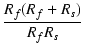 =
= 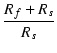 =
= |
|
(366) |
この結果を使うと,負帰還を掛けた後の伝達関数 Af(s) は,
| Af(s) | = | 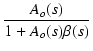 |
|
| = | 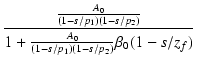 |
||
| = | 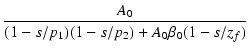 |
||
| = | 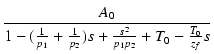 |
||
| = | 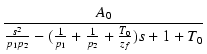 |
||
| = | 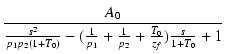 |
(367) |
| Q |
= | - 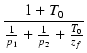 |
|
| = | - 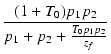 |
||
| = | - 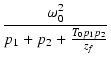 |
||
| Q | = | - 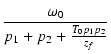 |
|
p1 + p2 + 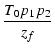 |
= | - |
|
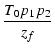 |
= | - |
|
| zf | = | - 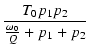 |
(370) |
まとめると,
| = | (371) | ||
| zf | = | - 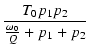 (作成するゼロの角周波数) (作成するゼロの角周波数) |
(372) |
| Cf | = | (373) |
モデルアンプの場合,
Rf = 9 kΩ とすれば,
| p1 | = | -2 |
|
| p2 | = | -2 |
|
| = | |||
| zf | = | - 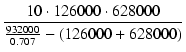 = - 1.40 [Mrad /s] = - 223 [kHz] = - 1.40 [Mrad /s] = - 223 [kHz] |
|
| Cf | = | 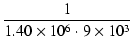 = 79.4 x 10-12 [F] = 79.4 x 10-12 [F] |
微分補償を行った場合,図130のように, ゲイン交点周波数は,137kHz になり,そのときの位相は -107o, 位相余裕は 73o になります.
微分補償による狭帯域化のシミュレーションを,図131に示します.
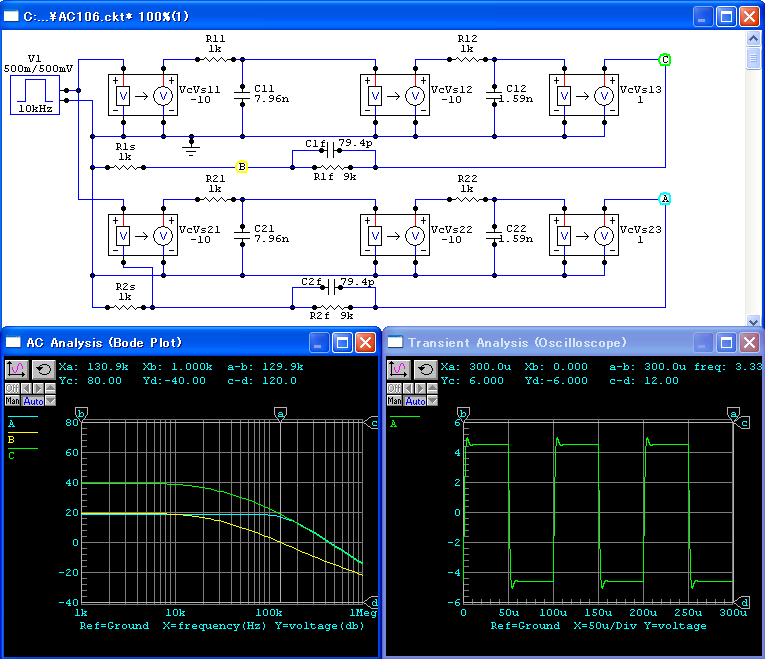
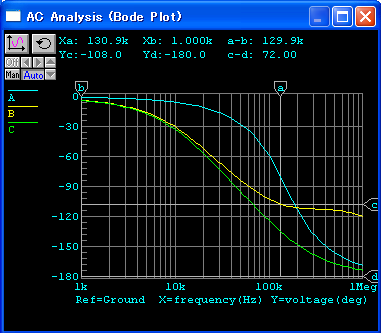
これまでの位相補償の結果をまとめると, 次の表のようになります.
| 方法 | ゲイン交点周波数 | 位相余裕 | 帰還後カットオフ周波数 |
| 補償なし | 124kHz | 48o | 203kHz |
| 狭帯域化 | 45.3kHz | 72o | 74kHz |
| ラグリード補償 | 90.5kHz | 72o | 148kHz |
| 微分型補償 | 137kHz | 73o | 155kHz |