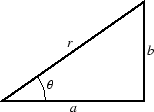
 |
| sin |
= | (377) | |
| cos |
= | (378) | |
| tan |
= | (379) |
|
|
(380) |
sin2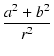 = 1 = 1
|
(381) |
| = | cos x | (382) | |
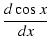 |
= | -sin x | (383) |
| = | -cos x | (384) | |
| = | sin x | (385) |
| sin(a |
= | sin a cos b |
(386) |
| cos(a |
= | cos a cos b |
(387) |
| tan(a |
= | 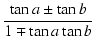 |
(388) |
| ejx | = | cos x + j sin x | (389) |
| cos x | = | 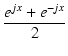 |
(390) |
| sin x | = | 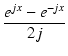 |
(391) |
| sinh x | = | 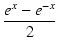 |
(392) |
| cosh x | = | 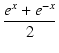 |
(393) |
| tanh x | = | (394) |
|
F(s) = |
(395) |
入力信号をラプラス変換したものと伝達関数とを掛け合わせたものを ラプラス逆変換すると,出力信号が得られます.
| F(s) | f (t) |
| 1 | impulse |
|
|
1 (unit step) |
|
|
e-at |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
te-at |
|
|
te-at(1 - at) |
|
|
|
|
|
cosh(at) |
|
|
|
|
|
cos(at) |
|
|
|
|
|
e-bt |
|
|
|
|
|
|
|
|
|
| F(s) | = | 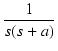 |
|
| = | |||
| = | |||
| f (t) | = |
| F(s) | = | 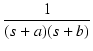 |
|
| = | |||
| = | |||
| f (t) | = |
| F(s) | = | ||
| = | |||
| = | |||
| f (t) | = |
| F(s) | = | 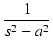 |
|
| = | 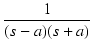 |
||
| = | |||
| = | |||
| f (t) | = | ||
| = |
| F(s) | = | ||
| = | |||
| = | |||
| = | |||
| f (t) | = | ||
| = | cosh at |
| F(s) | = | 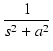 |
|
| = | 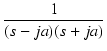 |
||
| = | |||
| = | |||
| f (t) | = | ||
| = |
| F(s) | = | ||
| = | |||
| = | |||
| = | |||
| f (t) | = | ||
| = | cos at |
| F(s) | = | 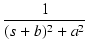 |
|
| = | 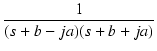 |
||
| = | 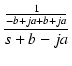 + + 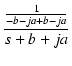 |
||
| = | 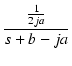 + + 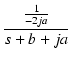 |
||
| = | 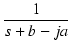 - - 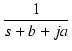 |
||
| f (t) | = | ||
| = | |||
| = | |||
| = |
| F(s) | = | ||
| = | |||
| = | 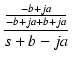 + + 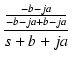 |
||
| = | 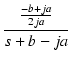 + + 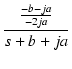 |
||
| = | 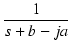 + + 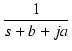 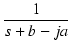 - - 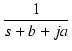 |
||
| f (t) | = | ||
| = | |||
| = | |||
| = | + e-btcos at - |
||
| = | e-bt |
| F(s) | = | 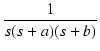 |
|
| = | 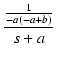 + + 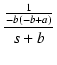 |
||
| = | |||
| = | 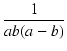 |
||
| f (t) | = | 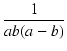 ((a - b) + be-at - ae-bt) ((a - b) + be-at - ae-bt) |
| F(s) | = | ![$\displaystyle {\frac{{1}}{{s[(s+b)^2+a^2]}}}$](img971.png) |
|
| = | 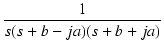 |
||
| = | 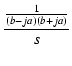 + + 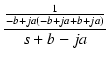 + + 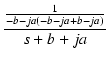 |
||
| = | 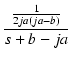 + + 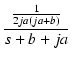 |
||
| = | 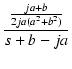 - - 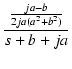 |
||
| = | 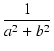 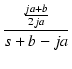 - - 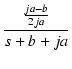 |
||
| = | 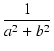 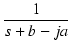 + + 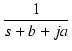 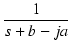 - - 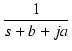 |
||
| f (t) | = | 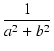 |
|
| = | 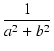 |
||
| = | 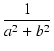 |
||
| = | 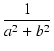 |
F(s) = 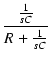 = = 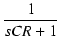 = = 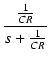 = = |
(396) |
| V2(s) | = | F(s)V1(s) | |
| = | F(s) | ||
| = | |||
| v2(t) | = |
| V2(s) | = | F(s)V1(s) | |
| = | F(s) . |
||
| = | |||
| v2(t) | = | 1 - e- |
F(s) = 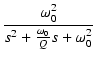
|
(397) |
| p | = | - 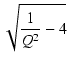 |
|
| = | |||
| p1 + p2 | = | 2 |
|
| p1 - p2 | = | 2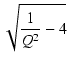 |
| V2(s) | = | F(s) | |
| = | 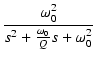 |
||
| = | 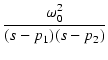 |
||
| v2(t) | = | 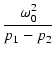 (ep1t - ep2t) (ep1t - ep2t) |
|
| = | |||
| = | |||
| = | 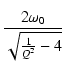 e e |
| V2(s) | = | ||
| = | 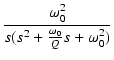 |
||
| = | 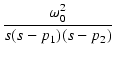 |
||
| v2(t) | = | 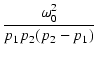 [(p2 - p1) - p2ep1t + p1ep2t] [(p2 - p1) - p2ep1t + p1ep2t] |
|
| = | 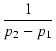 [(p2 - p1) - p2e( [(p2 - p1) - p2e( |
||
| = | 1 - 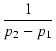 e e |
||
| = | 1 + |
||
| = | 1 + |
||
| = | 1 + |
| V2(s) | = | F(s) | |
| = | 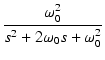 |
||
| = | 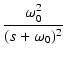 |
||
| v2(s) | = |
| V2(s) | = | ||
| = | 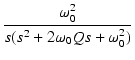 |
||
| = | 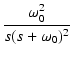 |
||
| v2(t) | = | 1 - e- |
|
| = | 1 - e- |
| b | = | ||
| a | = | 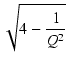 |
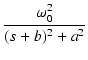
| V2(s) | = | F(s) | |
| = | 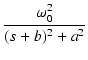 |
||
| v2(t) | = | ||
| = | 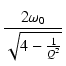 e- e-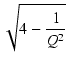 t t |
| V2(s) | = | ||
| = | ![$\displaystyle {\frac{{\omega_0^2}}{{s[(s+b)^2+a^2]}}}$](img661.png) |
||
| v2(t) | = | 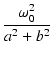 [1 - e-bt(cos at + [1 - e-bt(cos at + |
|
| = | 1 - |