

Next: この文書について...
Up: 定インピーダンスアッテネータとフィルタ
Previous: 2 アッテネータ
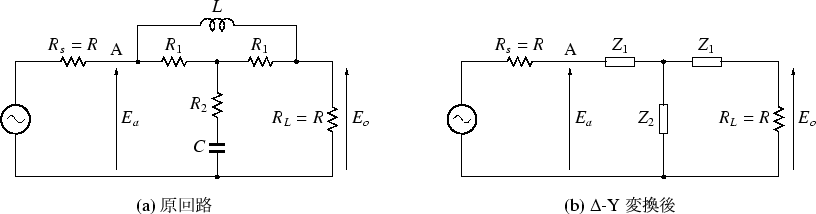
定インピーダンスアッテネータの入出力間に L を,
共通端子とグラウンドの間に C を入れると,
ローパスフィルタになります(図5).
図 5:
定インピーダンスLPF
 |
L と R1 の部分を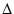 -Y変換すると,
変換後の Z1 および Z2 は,
-Y変換すると,
変換後の Z1 および Z2 は,
A点から右を見たインピーダンス Z が R で一定となる条件は,
式(18)より,
| R2 |
= |
Z1(Z1 +2Z2) |
|
| |
= |
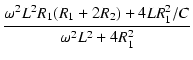 + j + j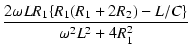 |
(30) |
この式は,以下の条件のときに,すべての周波数について成り立ちます.
R2 = R1(R1 +2R2) = 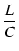
|
(31) |
このときの伝達関数 A は,
L = CR2 より,
| A |
= |
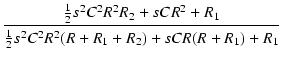 |
|
| |
= |
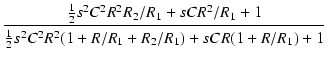 |
|
アッテネータの場合と同様に、
| R1 |
= |
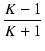 R R |
(32) |
| R2 |
= |
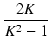 R R |
(33) |
とすれば,
となり,ゲインは
T1 = KCR/(K - 1) より下がり始め,
T2 = CR/(K - 1) で 1/K になり,それ以降は平坦になります.
K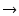
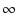 のときは,
のときは,
A = 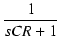
|
(35) |
となり,ゲインは T = CR より下がり始めます。
RIAAイコライザの時定数は,
| T1 |
= |
3180 μs |
(36) |
| T2 |
= |
318 μs |
(37) |
| T3 |
= |
75 μs |
(38) |
です.
T1, T2 は10倍離れているので,K = 10 であり,
R = 600 Ω とすれば,
| R1 |
= |
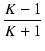 R = R = 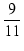 600 = 490.91 [Ω] 600 = 490.91 [Ω] |
|
| R2 |
= |
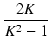 R = R = 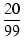 600 = 121.21 [Ω] 600 = 121.21 [Ω] |
|
| T1 |
= |
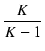 CR CR |
|
| C |
= |
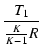 = = 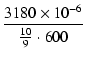 = 4.77 [μF] = 4.77 [μF] |
|
| L |
= |
CR2 = 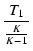 R = R = 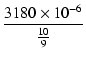 600 = 1.7172 [H] 600 = 1.7172 [H] |
|
高域のロールオフは,
K = 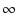 として,
として,
| R1 |
= |
R = 600 [Ω] |
|
| R2 |
= |
0 [Ω] |
|
| T3 |
= |
CR |
|
| C |
= |
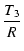 = = 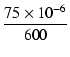 = 0.125 [μF] = 0.125 [μF] |
|
| L |
= |
T3R = 75 x 10-6 . 600 = 45 [mH] |
|
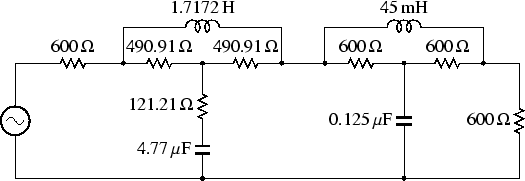
最終的な回路は,図6のようになります。
図 6:
定インピーダンスRIAAイコライザ
 |


Next: この文書について...
Up: 定インピーダンスアッテネータとフィルタ
Previous: 2 アッテネータ
Ayumi Nakabayashi
平成19年7月1日

![]() -Y変換すると,
変換後の Z1 および Z2 は,
-Y変換すると,
変換後の Z1 および Z2 は,
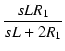
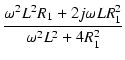
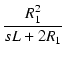 + R2 +
+ R2 + 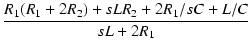
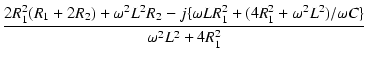
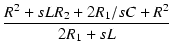
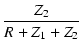
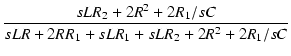
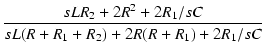
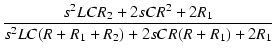
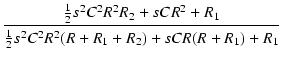
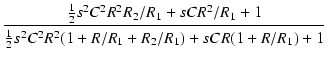
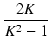 R
R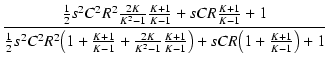
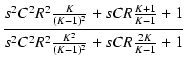 =
= 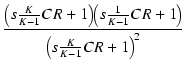
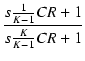
![]()
![]() のときは,
のときは,
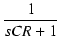
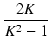 R =
R = 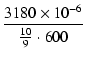 = 4.77 [μF]
= 4.77 [μF]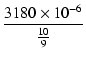 600 = 1.7172 [H]
600 = 1.7172 [H]![]() として,
として,
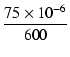 = 0.125 [μF]
= 0.125 [μF]