| vi | = | i1(R1 + R3) - i2R3 | |
| i1 | = | 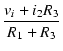 |
(6) |
式(1)より,
| = | - i1R3 + i2(rp + R2 + R3) - i3rp | ||
| (1 + |
= | i2{rp + R2 + (1 + |
(7) |
| = | i2rp - i3(rp + RL) | ||
| = | i2(rp + |
(8) |
(1 + 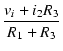 R3 R3 |
= | i2{rp + R2 + (1 + |
|
(1 +  vi vi |
= | i2 |
|
(1 +  vi vi |
= | i2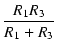 |
|
(1 +  vi vi |
= | i2{rp + R2 + (1 + |
|
| i2 | = | 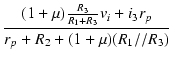 |
(9) |
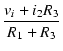 R3 R3 |
= | i2(rp + |
|
 vi vi |
= | i2 |
|
 vi vi |
= | i2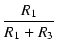 R3 R3 |
|
 vi vi |
= | i2{rp + |
(10) |
 vi vi |
= | 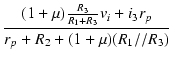 {rp + {rp + |
|
 vi vi |
= | 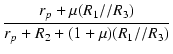  vi + i3rp vi + i3rp |
 vi vi |
= | x vi + i3rp vi + i3rp |
|
| i3{(1 - x)rp + RL} | = | - { vi vi |
|
| i3 | = | - 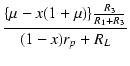 vi vi |
|
| i3 | = | -  . . 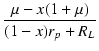 vi vi |
(11) |