| (1 - x * )rp + RL | = |  { { |
|
| rp + RL - rpx * | = |  RL - (1 + RL - (1 +  RLx * RLx * |
|
 RL - rp RL - rp |
= |  RL - RL - rp RL - RL - rp |
|
| x * | = | 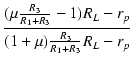 |
(14) |
| (1 - x * )rp + RL | = |  { { |
|
| rp + RL - rpx * | = |  RL - (1 + RL - (1 +  RLx * RLx * |
|
 RL - rp RL - rp |
= |  RL - RL - rp RL - RL - rp |
|
| x * | = | 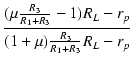 |
(14) |
| x * | = | 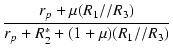 |
|
| {rp + R2 * + (1 + |
= | rp + |
|
| x(1 + |
= | (1 - x * )rp + { |
|
| R2 * | = | ||
| = | (15) |
| = | 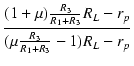 - 1 - 1 |
||
| = | 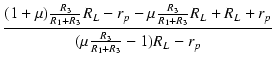 |
||
| = | 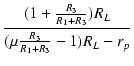 |