next up previous
Next: この文書について... Up: オートバランス位相反転回路 Previous: 7 R3 のとき

8 シミュレーション例

8.1 R3 がある回路

シミュレーションの回路図は，図3のようになります．

sim_sch1.png

図 3: シミュレーション回路1
\begin{figure}. % \end{figure}
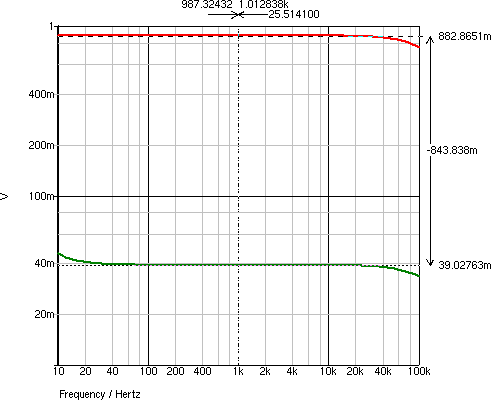
Vo と Vg の周波数特性は，図4のようになり， ゲインは0.8829となります．

sim_freq1.png

図 4: ゲインの周波数特性1
\begin{figure}. % \end{figure}
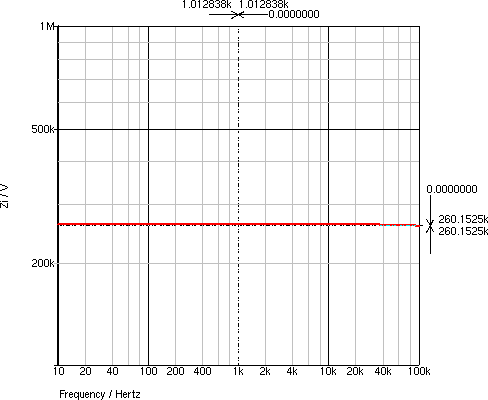
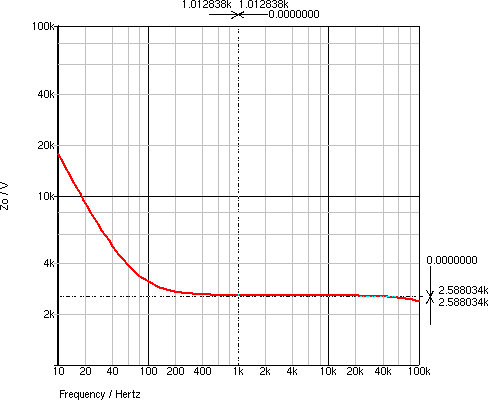
入力インピーダンスの周波数特性は，図5のようになり， Zi = 260.2 kΩ となります． 出力インピーダンスの周波数特性は，図6のようになり， Zo = 2.588 kΩ となります．

sim_Zi1.png

図 5: 入力インピーダンスの周波数特性1
\begin{figure}. % \end{figure}

sim_Zo1.png

図 6: 出力インピーダンスの周波数特性1
\begin{figure}. % \end{figure}
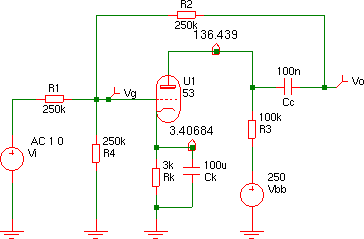
この回路の動作条件および三定数は，

Ep0 133.0312 V =              
Eg0 -3.406857 V =              
Ip0 1.135619 mA =              

で，
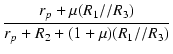x = $\displaystyle {\frac{{r_p + \mu (R_1//R_3)}}{{r_p + R_2 + (1 + \mu) (R_1//R_3)}}}$  
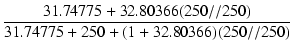  = $\displaystyle {\frac{{31.74775 + 32.80366 (250 // 250)}}{{31.74775 + 250 + (1 + 32.80366) (250 // 250)}}}$ = 0.9168  
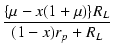A = - $\displaystyle {\frac{{R_3}}{{R_1 + R_3}}}$ . $\displaystyle {\frac{{\{\mu - x (1 + \mu)\} R_L}}{{(1 - x) r_p + R_L}}}$  
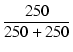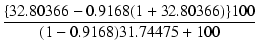  = - $\displaystyle {\frac{{250}}{{250 + 250}}}$ . $\displaystyle {\frac{{\{32.80366 - 0.9168 (1 + 32.80366)\} 100}}{{(1 - 0.9168) 31.74475 + 100}}}$ = - 0.8829  
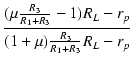x * = $\displaystyle {\frac{{(\mu \frac{R_3}{R_1 + R_3} - 1) R_L - r_p}}{{(1 + \mu) \frac{R_3}{R_1 + R_3} R_L - r_p}}}$  
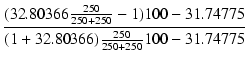  = $\displaystyle {\frac{{(32.80366 \frac{250}{250 + 250} - 1) 100 - 31.74775}}{{(1 + 32.80366) \frac{250}{250 + 250} 100 - 31.74775}}}$ = 0.90955  
R2 * = 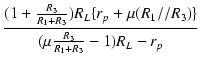$\displaystyle {\frac{{(1 + \frac{R_3}{R_1 + R_3}) R_L \{r_p + \mu (R_1//R_3)\} }}{{(\mu \frac{R_3}{R_1 + R_3} - 1) R_L - r_p}}}$ - (R1//R3)  
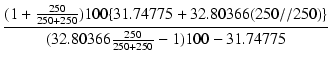  = $\displaystyle {\frac{{(1 + \frac{250}{250 + 250}) 100 \{31.74775 + 32.80366 (250//250)\} }}{{(32.80366 \frac{250}{250 + 250} - 1 ) 100 - 31.74775}}}$ - (250//250)  
  = 285.9 [kΩ]  
Zi = 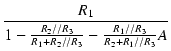$\displaystyle {\frac{{R_1}}{{1 - \frac{R_2 // R_3}{R_1 + R_2 // R_3} - \frac{R_1 // R_3}{R_2 + R_1 // R_3} A}}}$  
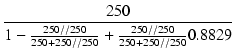  = $\displaystyle {\frac{{250}}{{1 - \frac{250 // 250}{250 + 250 // 250} + \frac{250 // 250}{250 + 250 // 250} 0.8829}}}$ = 260.2 [kΩ]  
Zo = (R2 + R1//R3)//RL//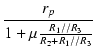$\displaystyle {\frac{{r_p}}{{1 + \mu \frac{R_1//R_3}{R_2 + R_1//R_3}}}}$  
  = (250 + 125)//100//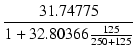$\displaystyle {\frac{{31.74775}}{{1 + 32.80366 \frac{125}{250 + 125}}}}$ = 2.573 [kΩ]  

8.2 R3 がない回路

シミュレーションの回路図は，図7のようになります．

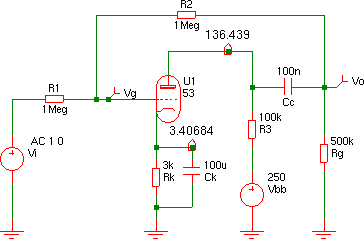
sim_sch2.png

図 7: シミュレーション回路2
\begin{figure}. % \end{figure}
Vo と Vg の周波数特性は，図8のようになり， ゲインは0.9202となります．

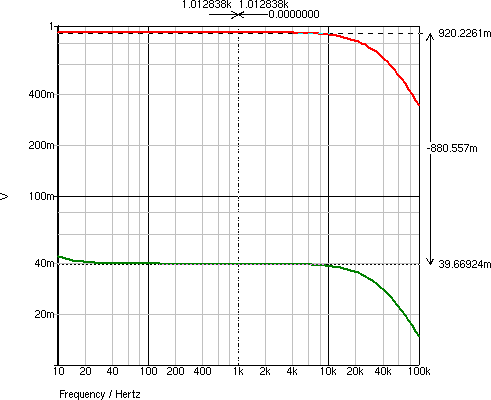
sim_freq2.png

図 8: ゲインの周波数特性2
\begin{figure}. % \end{figure}
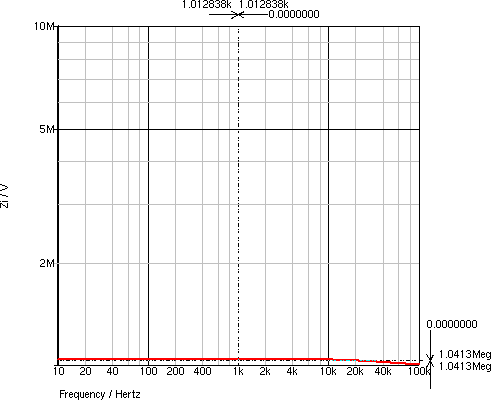
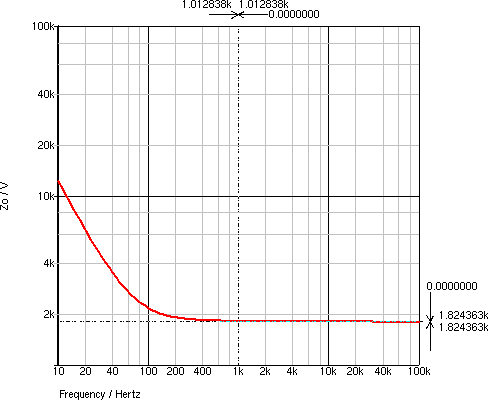
入力インピーダンスの周波数特性は，図9のようになり， Zi = 1041 kΩ となります． 出力インピーダンスの周波数特性は，図10のようになり， Zo = 1.824 kΩ となります． RL = Rp//Rg = 100//500 = 83.333 kΩ です．
x = 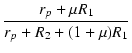$\displaystyle {\frac{{r_p + \mu R_1}}{{r_p + R_2 + (1 + \mu) R_1}}}$  
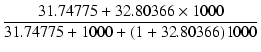  = $\displaystyle {\frac{{31.74775 + 32.80366 \times 1000}}{{31.74775 + 1000 + (1 + 32.80366) 1000}}}$ = 0.94259  
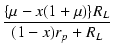A = - $\displaystyle {\frac{{\{\mu - x (1 + \mu)\} R_L}}{{(1 - x) r_p + R_L}}}$  
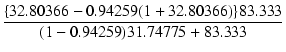  = - $\displaystyle {\frac{{\{32.80366 - 0.94259 (1 + 32.80366)\} 83.333}}{{(1 - 0.94259) 31.74775 + 83.333}}}$ = - 0.9206  
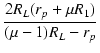R2 * = $\displaystyle {\frac{{2 R_L(r_p + \mu R_1)}}{{(\mu - 1) R_L - r_p}}}$ - R1  
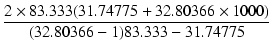  = $\displaystyle {\frac{{2 \times 83.333(31.74775 + 32.80366 \times 1000)}}{{(32.80366 - 1) 83.333 - 31.74775}}}$ -1000 = 1090 [kΩ]  
Zi = 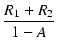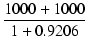$\displaystyle {\frac{{R_1 + R_2}}{{1 - A}}}$ = $\displaystyle {\frac{{1000 + 1000}}{{1 + 0.9206}}}$ = 1041 [kΩ]  
Zo = (R1 + R2)//RL//$\displaystyle {\frac{{r_p}}{{1 + \mu \frac{R_1}{R_1 + R_2}}}}$  
  = (1000 + 1000)//83.333//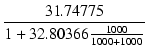$\displaystyle {\frac{{31.74775}}{{1 + 32.80366 \frac{1000}{1000 + 1000}}}}$ = 1.783 [kΩ]  

sim_Zi2.png

図 9: 入力インピーダンスの周波数特性2
\begin{figure}. % \end{figure}

sim_Zo2.png

図 10: 出力インピーダンスの周波数特性2
\begin{figure}. % \end{figure}

next up previous
Next: この文書について... Up: オートバランス位相反転回路 Previous: 7 R3 のとき
Ayumi Nakabayashi
平成19年11月17日