Next: この文書について... Up: エレクトレット・コンデンサ・マイクBM-800の改良 Previous: 2 BM-800の特性
| = | 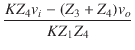 - - 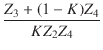 vo vo |
||
| Z1Z2vo | = | KZ2Z4vi - Z2(Z3 + Z4)vo - Z1{Z3 + (1 - K)Z4}vo | |
| {Z1Z2 + Z2(Z3 + Z4) + Z1Z3 + (1 - K)Z1Z4}vo | = | KZ2Z4vi | |
| vo | = | 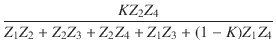 vi vi |
|
| = | 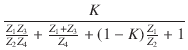 vi vi |
(11) |
| Z1 | = | R1 | |
| Z2 | = | ||
| Z3 | = | R2 | |
| Z4 | = |
| Z1 | = | ||
| Z2 | = | R1 | |
| Z3 | = | ||
| Z4 | = | R2 |
ayumi