| = | |||
| = | G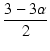 |
||
| + Ep |
|||
| = | G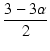 |
||
x 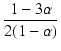 . . 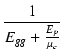 |
|||
| = | 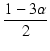 . . 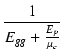 |
(B.4) |
§≥§≥§«°§¡∞Ω“§∑§øª∞∂À¥…§Œ∆√¿≠∂ ¿˛§Œ∆√ƒß§¨À˛§ø§µ§Ï§∆§§§Î§´°§ƒ¥§Ÿ§∆§þ§Þ§π°• §Þ§∫°§1§«§π§¨°§ º∞(B.1)§Ë§Í°§ •◊•Ï°º•»≈≈ŒÆ Ip §œ Eg = - 0.6 §Œ§»§≠§À Ep §Œ1.5æ˧À»ÊŒ„§∑§Þ§π°•
2§À¥ÿ§∑§∆§«§π§¨°§
•´•√•»•™•’§Œ§»§≥§Ì§«§œ°§
º∞(B.1)§Ë§Í
Egg + Ep/![]() = 0 §«§π§´§È°§
= 0 §«§π§´§È°§
![]() §œ
§œ ![]() §»§ §Í§Þ§π°•
§»§ §Í§Þ§π°•
3§À§ƒ§§§∆§œ°§
º∞(B.5)§Œ Egg §À0§Ú¬Â∆˛§π§Î§»°§§≥§Ï§¨ ![]() §»§ §Í°§
§»§ §Í°§
4§Œ¥ÿ∑∏§¨¿ÆŒ©§π§Î§´§…§¶§´§Úƒ¥§Ÿ§Þ§π°•
º∞(B.1), (B.2)§Ú
Egg + Ep/![]() §À§ƒ§§§∆≤Ú§≠§Þ§π°•
º∞(B.1)§Ë§Í°§
§À§ƒ§§§∆≤Ú§≠§Þ§π°•
º∞(B.1)§Ë§Í°§
§≥§Ï§Þ§«§œ
Egg![]() 0 §ŒæÏπÁ§À§ƒ§§§∆πÕ§®§∆§≠§Þ§∑§ø§¨°§
§≥§≥§«°§Egg > 0 §ŒæÏπÁ§ÚπÕ§®§Þ§π°•
Egg > 0 §ŒæÏπÁ°§•§•Û•º•Î∏˙≤ÃB.2§ÚπÕ§®§ §Ø§∆§‚§Ë§§§Œ§«°§
0 §ŒæÏπÁ§À§ƒ§§§∆πÕ§®§∆§≠§Þ§∑§ø§¨°§
§≥§≥§«°§Egg > 0 §ŒæÏπÁ§ÚπÕ§®§Þ§π°•
Egg > 0 §ŒæÏπÁ°§•§•Û•º•Î∏˙≤ÃB.2§ÚπÕ§®§ §Ø§∆§‚§Ë§§§Œ§«°§![]() §œ
§œ ![]() §«∞σͧ»≤æƒÍ§∑§Þ§π°•
§«∞σͧ»≤æƒÍ§∑§Þ§π°•
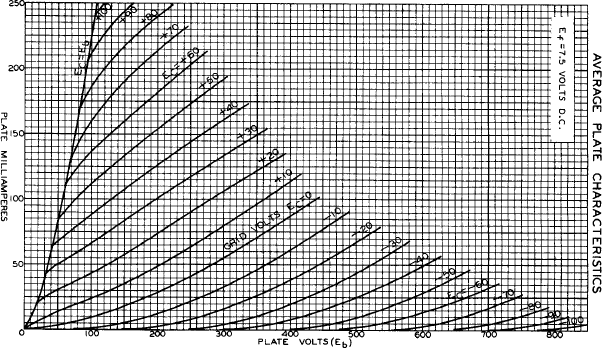
ª∞∂À¥…§Œ•´•Ω°º•…§´§ÈŒÆ§Ï§Î≈≈ŒÆ§œ°§ •∞•Í•√•…§Œ∞Ã√÷§À•◊•Ï°º•»§¨§¢§Î∆Û∂À¥…(≈˘≤¡∆Û∂À¥…)§ÚπÕ§®°§ §Ω§Œ•◊•Ï°º•»≈≈∞µ(Õ≠∏˙≈≈∞µ)§Ú
§»§∑§∆πÕ§®§Þ§π°• •∞•Í•√•…≈≈∞µ§¨¿µ§ŒŒŒ∞˧«§œ•§•Û•º•Î∏˙≤çÚπÕ§®§Î…¨Õ◊§¨§ §§§Œ§«°§ ≈˘≤¡∆Û∂À¥…§Œ•◊•Ï°º•»≈≈ŒÆ(•´•Ω°º•…≈≈ŒÆ)§œ°§•◊•Ï°º•»≈≈∞µ§Œ1.5æ˧À»ÊŒ„§∑§Þ§π°• §∑§ø§¨§√§∆°§•´•Ω°º•…≈≈ŒÆ§œ°§ §»…Ω§ª§Þ§π°• §≥§≥§«°§G' §œ≈˘≤¡∆Û∂À¥…§Œ•—°º•”•¢•Û•π§«§π°•G' §Úµ·§·§Þ§π°• Egg = 0 §Œ§»§≠§Œ Ip §œ°§º∞(B.1)§Ë§Í°§
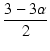
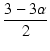
•∞•Í•√•…≈≈∞µ§Ú —§®§øæÏπÁ§Œ°§•◊•Ï°º•»≈≈∞µ§»•´•Ω°º•…≈≈ŒÆ§Œ¥ÿ∑∏§Ú•∞•È•’§À…٧𧻰§ øÞB.1§Œ§Ë§¶§À§ §Í§Þ§π°•
•∞•Í•√•…≈≈∞µ§¨ 0V §Œ§»§≠§œ°§•◊•Ï°º•»≈≈∞µ§¨ 0V §Œ§»§≥§Ì§´§È •◊•Ï°º•»≈≈ŒÆ§¨ŒÆ§Ïªœ§·§Þ§π°• •∞•Í•√•…≈≈∞µ§¨ Eg (> 0)§Œ§»§≠§œ°§ •◊•Ï°º•»≈≈∞µ§¨ -
|
xg |
(B.13) |
§Þ§ø Ep = Eg §Œ•´°º•÷§œ•◊•Ï°º•»≈≈∞µ§Œ1.5æ˧À»ÊŒ„§∑§∆§§§Þ§π°• §≥§Ï§È§´§È°§•◊•Ï°º•»≈≈∞µ§ÚÕø§®§øª˛§ÀŒÆ§Ï§¶§Î∫«¬Á§Œ•◊•Ï°º•»≈≈ŒÆ Ip lim §Úº°§Œº∞§«…Ω§π§≥§»§¨§«§≠§Þ§π°• §≥§≥§«°§Glim §œ•◊•Ï°º•»≈≈ŒÆ§Ú¿©∏¬§π§Î∞ϺԧŒ•—°º•”•¢•Û•π§»πÕ§®§È§Ï§Þ§π°•
§≥§Œ xg §™§Ë§” Glim §œ°§
Ep* = Eg* §Œ•◊•Ï°º•»≈≈ŒÆ Ip* §™§Ë§” •∞•Í•√•…≈≈ŒÆ Ig* §Œ•«°º•ø§¨§¢§Ï§–§Ω§Ï§ÚÕ—§§§∆°§
| xg | = | 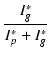 |
(B.15) |
| Glim | = | 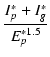 |
(B.16) |
Ep![]() Eg §Œ§»§≠°§•´•Ω°º•…§´§È ¸Ω–§µ§Ï§ø≈≈ª“§œ•∞•Í•√•…§™§Ë§”•◊•Ï°º•»§À§Ë§√§∆
∫ӧȧϧÎ≈≈≥¶§À§Ë§√§∆≤√¬Æ§µ§Ï°§∞Ï…Ù§œ•∞•Í•√•…§ÀŒÆ§Ïπ˛§þ°§ªƒ§Í§œ§µ§È§À≤√¬Æ§µ§Ï§∆•◊•Ï°º•»§ÀŒÆ§Ï§Þ§π°•
•◊•Ï°º•»≈≈∞µ§¨π‚§Ø§ §Ï§–§ §Î§€§…°§•∞•Í•√•…§ÀŒÆ§Ïπ˛§ý≈≈ŒÆ§œæا §Ø§ §Í§Þ§π°•
Eg §Œ§»§≠°§•´•Ω°º•…§´§È ¸Ω–§µ§Ï§ø≈≈ª“§œ•∞•Í•√•…§™§Ë§”•◊•Ï°º•»§À§Ë§√§∆
∫ӧȧϧÎ≈≈≥¶§À§Ë§√§∆≤√¬Æ§µ§Ï°§∞Ï…Ù§œ•∞•Í•√•…§ÀŒÆ§Ïπ˛§þ°§ªƒ§Í§œ§µ§È§À≤√¬Æ§µ§Ï§∆•◊•Ï°º•»§ÀŒÆ§Ï§Þ§π°•
•◊•Ï°º•»≈≈∞µ§¨π‚§Ø§ §Ï§–§ §Î§€§…°§•∞•Í•√•…§ÀŒÆ§Ïπ˛§ý≈≈ŒÆ§œæا §Ø§ §Í§Þ§π°•
Ep < Eg §Œ§»§≠°§•∞•Í•√•…§ÚƒÃ§Í≤·§Æ§ø≈≈ª“§œ°§•∞•Í•√•…-•◊•Ï°º•»¥÷§Œ≈≈≥¶§À§Ë§√§∆∏∫¬Æ§µ§ª§È§Ï°§∞Ï…Ù§œ•◊•Ï°º•»§À≈˛√£§∑§Þ§π§¨°§•∞•Í•√•…§À÷§√§∆§Ø§Î≈≈ª“§‚§¢§Í§Þ§π°• §∑§ø§¨§√§∆°§•◊•Ï°º•»≈≈∞µ§¨ƒ„§Ø§ §Ï§–§ §Î§€§…°§•∞•Í•√•…≈≈ŒÆ§¨¡˝§®§Þ§π°•
§≥§Œ§Ë§¶§π§Ú…Ω§π§Œ§¨¥ÿøÙ fg(Ep) §«°§ Ep = Eg §Œ§»§≠§Œ•∞•Í•√•…≈≈ŒÆ§Ú¥Ωý§»§∑§∆°§ §µ§Þ§∂§Þ§ •◊•Ï°º•»≈≈∞µ§À¬–§π§Î•∞•Í•√•…≈≈ŒÆ§Œ¡Í¬–≈™§ ¬Á§≠§µ§Ú…Ω§∑§∆§§§Þ§π(øÞB.3)°•
fg(Ep) = 1.2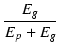 + 0.4 + 0.4
|
(B.17) |
| Ig = xgGlimEg1.5fg(Ep) | (B.18) |
§≥§≥§«°§•∞•Í•√•…≈≈ŒÆ§Œ•«°º•ø§¨§ §§æÏπÁ§Œ•∞•Í•√•…≈≈ŒÆ§Œø‰ƒÍ ˝À°§ÚΩ“§Ÿ§Þ§π°• •◊•Ï°º•»≈≈∞µ§¨•∞•Í•√•…≈≈∞µ§Ë§Íπ‚§§æÏπÁ°§ •´•Ω°º•…≈≈ŒÆ§œøÞB.4§Œ Ik §Œ•´°º•÷§Œ§Ë§¶§À§ §Í§Þ§π(º∞(B.11))°•
•◊•Ï°º•»≈≈∞µ§¨0§»§ §√§øæÏπÁ°§ •´•Ω°º•…≈≈ŒÆ§œ•∞•Í•√•…≈≈ŒÆ§»≈˘§∑§Ø°§Ik §Œ•´°º•÷§»yº¥§Œ∏Ú≈¿ Ik0 §Ë§Í§‚ƒ„§Ø§ §Í§Þ§π°• §≥§≥§«°§∑–∏≥≈™§À°§| Ig0 = 0.8Ik0 | (B.19) |
º∞(B.11)§Úª»§√§∆ Ik0, Ik1, Ig1 §Úµ·§·§Î§»°§
| Ik0 | = | G'Eg1.5 | |
| Ik1 | = | G' |
|
| Ig1 | = | 0.5Ik0 = 0.5G'Eg1.5 |
| xg | = | 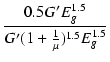 = = 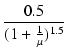 |
(B.20) |
| Glim | = | 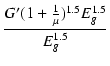 = G' = G' |
(B.21) |
| Ip = min(Ik - Ig, Ip lim) | (B.22) |
§≥§Ï§Þ§« Egg §œ Eg §Ë§Í§‚ÃÛ 0.6V π‚§§§»§∑§∆§§§Þ§∑§ø§¨°§ §≥§Œ√Õ§‚øø∂ı¥…§À§Ë§Í∞€§ §Î§Œ§«°§§≥§Ï§Ú Ego §»§∑§Þ§π°•
§Þ§ø°§| a | = | (B.24) | |
| b | = | (B.25) | |
| c | = | 3 |
(B.26) |
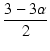 |
= | ||
| = | 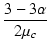 |
||
| = | 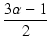 . . |
|
G' = G |
(B.27) |
§≥§Ï§È§Úª»§√§∆°§§≥§Ï§Þ§«§Œº∞§Ú§Þ§»§·§Þ§π°•