Ik1 = 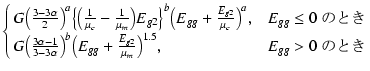
|
(B.32) |
五極管のプレート特性は,スクリーングリッド(G2)電圧によって変わってきますが, データシートには限られたスクリーングリッド電圧の特性しか掲載されていないため, さまざまなスクリーングリッド電圧の情報が含まれている三極管接続の特性をベースとします. まず,三極管接続の特性より,三極管接続のモデルのパラメータを求めます. 三極管接続では Ep = Eg2 ですから,この状況のプレート電流が判明します. この電流を Ep と Eg2 の大小関係によって適切に配分してやれば, 五極管のモデルを三極管接続したものと,三極管接続のモデルが一致します. プレート電圧とスクリーングリッド電圧では, スクリーングリッド電圧の影響のほうがはるかに大きいので, 一旦プレート電圧を無視して,スクリーングリッド電圧をプレート電圧とし, 三極管のモデルからカソード電流とグリッド電流を求めます.
この時点のカソード電流 Ik1 は,
Ik1 = 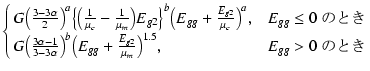
|
(B.32) |
グリッド電流は,
| Ig = xgGlimEg1.5fg(Ep) | (B.33) |
|
f (Ep, Eg2) = 1 - 0.4(e- |
(B.34) |
この関数の形状を,図B.6に示します. Ep = Eg2 のとき,この関数は 1 となり, Ep = 0 のとき,0.6 となります.
後で使うため,この関数を Ep と Eg2 で偏微分した関数も求めておきます.
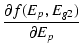 |
= | 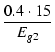 e- e- |
(B.35) |
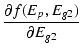 |
= | - 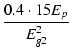 e- e- |
(B.36) |
この時点のカソード電流 Ik2 は,
| Ik2 = f (Ep, Eg2)(Ik1 - Ig) | (B.37) |
このカソード電流をプレートとG2に分配します. G2に分配する比率を g(Ep) という関数で表します.
g(Ep) = (1 - r)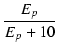 |
(B.38) |
この関数の形状を,図B.7に示します.
Ep = 0 のとき,この関数の値は 1 となり, Ep =この関数を用いて,スクリーングリッド電流は
| Ig2' = g(Ep)Ik2 | (B.39) |
この関数についても,Ep で微分した関数を求めておきます.
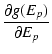 = = 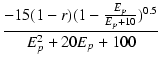
|
(B.40) |
ある Ep についての Ip, Ig2 から r を求めるには,
r = 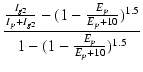
|
(B.41) |
プレート電流は,プレート電圧が高くなると増えますが, プレート電圧とG2電圧が等しいときのプレート電流を1としたときの比率を関数 h(Ep, Eg2) で表します.
h(Ep, Eg2) = 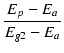
|
(B.42) |
この関数の形状を,図B.8に示します.
Ep = Ea のとき,この関数は 0 となり, Ep = Eg2 のとき,1 となります.この時点でのカソード電流は,次のようになります.
| Ik3 = h(Ep, Eg2)Ik2 | (B.43) |
偏微分した結果は,
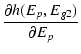 |
= | 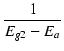 |
(B.44) |
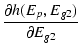 |
= | - 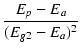 |
(B.45) |
前節のカソード電流から,プレート電流は,
| Ik lim | = | (1 - xg)Glimmax(Ep, Eg2)1.5 | (B.46) |
| Ik4 | = | min(Ik3, Ik lim) | (B.47) |
| Ip | = | max{min(Ik4 - Ig2', Ip lim), 0} | (B.48) |
| Ig2 = max(Ik4 - Ip, 0) | (B.49) |
三定数は,
| gm | = | 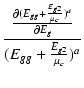 Ip = Ip = 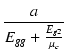 Ip Ip |
(B.50) |
| = | 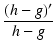 |
(B.51) | |
| gmg2 | = | 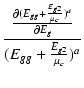 Ig2 = Ig2 = 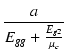 Ig2 Ig2 |
(B.52) |
| = | |||
| = | Ig2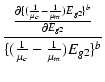 + + 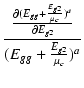 |
||
| = | Ig2 |
(B.53) | |
| μg1-g2' | = | (B.54) | |
| = | Ip |
(B.55) | |
| μg1-g2 | = | ||
| = | 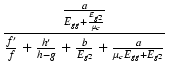 |
(B.56) |