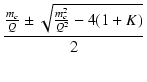

Next: 2 サレンキー型LPFの特性
Up: 多重帰還型LPFの現実的な定数を求める方法
Previous: 多重帰還型LPFの現実的な定数を求める方法
図 1:
多重帰還型LPFの回路
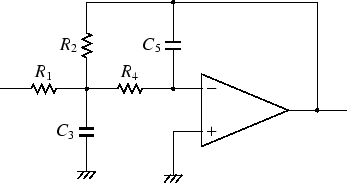 |
図1の回路の多重帰還型LPFの伝達特性と 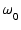 , Q の値は,
, Q の値は,
| T(s) |
= |
- 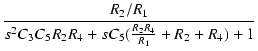 |
(1) |
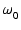 |
= |
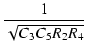 |
(2) |
| Q |
= |
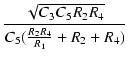 |
(3) |
となります.
通過域のゲインを
K = R2/R1 とおけば,
| T(s) |
= |
- 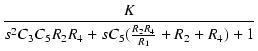 |
|
| Q |
= |
![$\displaystyle {\frac{{\sqrt{C_3 C_5 R_2 R_4}}}{{C_5[R_2 + (1 + K) R_4]}}}$](img8.png) |
|
となります.
ここで,
コンデンサおよび抵抗の比について,
| R2 |
= |
mrR |
|
| R4 |
= |
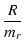 |
|
| C3 |
= |
mcC |
|
| C5 |
= |
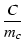 |
|
とおくと,
となります.
さまざまな K の値について,
mr を変えながら Q の値を描くと,
図2のようになります.
図 2:
mr に対する Q の値.(mc = 3 の場合)
|
|
図2は,mc = 3 の場合ですが,
Q は mc に比例するので,
異なった mc の値に関するグラフは,
図2の形状をそのまま上下にずらしたものになります.
常識的な
R1 = R2 = R4 の場合,
すなわち mr = 1 における値よりも大きな Q が得られる mr が
存在することがわかります.
この最大の Q となる mr を利用すれば,
一定の Q に対して mc の値を小さく済ませることができます.
指定された Q に対して mc が最小となるのは,
式(5)を mc について解いた式の,
mr に関する導関数値が 0 となる mr のときです.
| mc |
= |
Q[mr + (1 + K)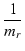 ] ] |
|
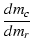 |
= |
Q[1 - (1 + K)mr-2] = 0 |
|
| mr |
= |
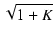 |
|
したがって,
| min mc |
= |
Q(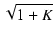 + + 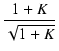 ) ) |
(6) |
| |
= |
2Q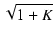 |
(7) |
これ以上の mc が確保されていれば,
mr を調整することによって,
Q の値を目的の値に下げることができます.
mr の値は,式(5)より,
mr + 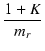 |
= |
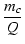 |
|
mr2 - 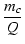 mr + (1 + K) mr + (1 + K) |
= |
0 |
|
| mr |
= |
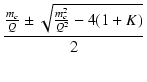 |
|
ここで,図2より,
mr は2つの解を持ちますが,
Q の極大値が必ず mr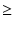 1 にあるので,
小さい方の解のほうが mr = 1 に近くなります.
抵抗の比は小さいほうが良いので,こちらの解を選びます.
1 にあるので,
小さい方の解のほうが mr = 1 に近くなります.
抵抗の比は小さいほうが良いので,こちらの解を選びます.


Next: 2 サレンキー型LPFの特性
Up: 多重帰還型LPFの現実的な定数を求める方法
Previous: 多重帰還型LPFの現実的な定数を求める方法
Ayumi Nakabayashi
平成24年7月21日

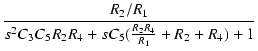
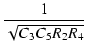
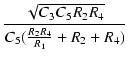
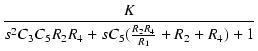
![$\displaystyle {\frac{{\sqrt{C_3 C_5 R_2 R_4}}}{{C_5[R_2 + (1 + K) R_4]}}}$](img8.png)
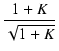 )
)