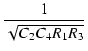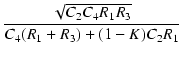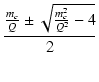

Next: 3 定数を求めるプログラム
Up: 多重帰還型LPFの現実的な定数を求める方法
Previous: 1 多重帰還型LPFの特性
図 3:
サレンキー型LPFの回路
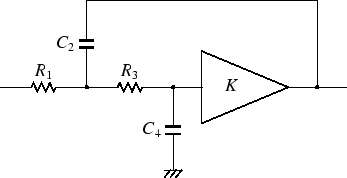 |
図3の回路のサレンキー型LPFの伝達特性と 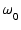 , Q の値は,
アンプのゲインを K とすると,
, Q の値は,
アンプのゲインを K とすると,
| T(s) |
= |
![$\displaystyle {\frac{{K}}{{s^2 C_2 C_4 R_1 R_3 + s [C_4(R_1 + R_3) + (1 - K) C_2 R_1] + 1}}}$](img24.png) |
(8) |
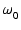 |
= |
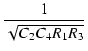 |
(9) |
| Q |
= |
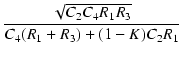 |
(10) |
となります.
しかし,サレンキー型LPFで K の値を大きくすると,
Q の値が敏感になりすぎるので,
ここでは K = 1 の場合のみを考えます.
ここで,
コンデンサおよび抵抗の比について,
| R1 |
= |
mrR |
|
| R3 |
= |
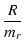 |
|
| C2 |
= |
mcC |
|
| C4 |
= |
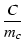 |
|
とおくと,
となります.
Q は mr = 1 のときに最大となります.
指定された Q に対する mc の最小値は,
で,これ以上の mc が確保されていれば,
mr を調整することによって,
Q の値を目的の値に下げることができます.
mr の値は,式(12)より,
mr + 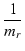 |
= |
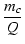 |
|
mr2 - 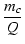 mr + 1 mr + 1 |
= |
0 |
|
| mr |
= |
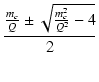 |
|
ここで,
mr は2つの解を持ちますが,
一方の解は他方の解の逆数となります.
R1 が大きいほうが前段の負荷が軽くなりますので,
ここでは mr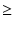 1 の解を選びます.
1 の解を選びます.


Next: 3 定数を求めるプログラム
Up: 多重帰還型LPFの現実的な定数を求める方法
Previous: 1 多重帰還型LPFの特性
Ayumi Nakabayashi
平成24年7月21日

![$\displaystyle {\frac{{K}}{{s^2 C_2 C_4 R_1 R_3 + s [C_4(R_1 + R_3) + (1 - K) C_2 R_1] + 1}}}$](img24.png)