


Next: A.2 分圧,分流
Up: A. 基礎知識
Previous: A. 基礎知識
図A.1に示すように,
抵抗 R に流れる電流を iR, R の両端子間の電圧を vR とすれば,
次の関係が成立します.
| vR |
= |
iRR |
(A.1) |
| iR |
= |
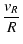 |
(A.2) |
| R |
= |
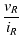 |
(A.3) |
これはオームの法則と呼ばれているものです.
図 A.1:
抵抗素子
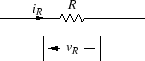 |
図A.2に示すように,
インダクタンスが L のインダクタに流れる電流 iL が,
時間 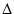 t の間に
t の間に
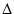 iL だけ増加する場合,
インダクタの両端子間の電圧 vL は,次の式で与えられます.
iL だけ増加する場合,
インダクタの両端子間の電圧 vL は,次の式で与えられます.
vL = L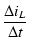
|
(A.4) |
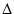 t
t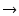 0 の極限をとれば,
0 の極限をとれば,
| vL |
= |
L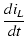 |
(A.5) |
| iL |
= |
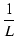 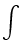 vL dt vL dt |
(A.6) |
図 A.2:
インダクタンス素子
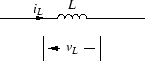 |
正弦波の場合,複素数表示で表すと,次のようになります.
| ZL |
= |
j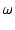 L L |
(A.7) |
| vL |
= |
iLZL |
(A.8) |
| iL |
= |
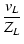 |
(A.9) |
| ZL |
= |
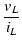 |
(A.10) |
ここで,j は虚数単位(j2 = - 1),
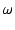 は角周波数(
は角周波数(
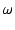 = 2
= 2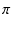 f),
f は周波数です.
f),
f は周波数です.
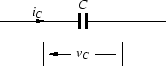
図A.3に示すように,
静電容量が C のコンデンサに電流 iL が時間 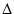 t だけ流れるとき,
コンデンサに蓄積される電荷 q の増加を
t だけ流れるとき,
コンデンサに蓄積される電荷 q の増加を 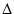 q とし,
コンデンサの端子電圧 vC の増加を
q とし,
コンデンサの端子電圧 vC の増加を
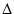 vC とすれば,
vC とすれば,
iC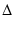 t t |
= |
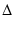 q = C q = C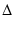 vC vC |
(A.11) |
| iC |
= |
C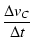 |
(A.12) |
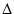 t
t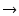 0 の極限をとれば,
0 の極限をとれば,
| iC |
= |
C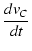 |
(A.13) |
| vC |
= |
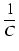 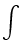 iC dt iC dt |
(A.14) |
図 A.3:
静電容量素子
 |
正弦波の場合,複素数表示で表すと,次のようになります.
| ZC |
= |
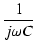 |
(A.15) |
| vC |
= |
iCZC |
(A.16) |
| iC |
= |
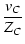 |
(A.17) |
| ZC |
= |
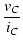 |
(A.18) |



Next: A.2 分圧,分流
Up: A. 基礎知識
Previous: A. 基礎知識
Ayumi Nakabayashi
平成19年6月28日