 |
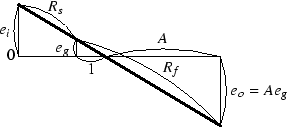
入力端子と出力端子の間の電圧は,ei + eo で, これが Rs + Rf の両端に加わっていることになります. 信号が加わっても常に 0 V になっている点があり, それは,Rf を 1 : A に内分した点です. A は負帰還が掛かっていない場合のゲインです. 入力信号 ei は,Rs と Rf/(1 + A) で分割され eg となって グリッドに加わります.
eg = 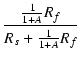 ei ei
|
(1) |
eo = Aeg = A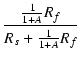 ei ei
|
(2) |
| Af | = | 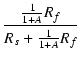 |
|
| = | 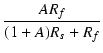 = = 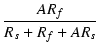 |
||
| = | 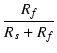 . . 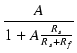 |
(3) |
通常の負帰還と同様に,
![]() = Rs/(Rs + Rf) とおくと,
= Rs/(Rs + Rf) とおくと,
A = (1 - 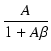
|
(4) |
まず,入力信号だけを考えます. このとき,出力電圧は0として,グリッドに生じる電圧を求めます. 図3 (a)より, グリッドにおける入力電圧 ei' は,
ei' = 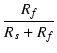 ei ei
|
(5) |
次に,出力信号だけを考えます. 入力電圧を0として,グリッドに生じる帰還電圧を求めます. 図3 (b)より, グリッドにおける帰還電圧 ef は,
ef = 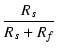 eo eo
|
(6) |
グリッドにおける入力電圧 ei' から帰還電圧 ef を引いたものが, 正味のグリッド入力 eg になり, その A 倍が出力 eo になります.
| eo = Aeg = A(ei' - ef) | (7) |
2つの図を重ね合わせると,図3 (c)のようになります.
すなわち,帰還率が
![]() = Rs/(Rs + Rf) の負帰還増幅器に,
ei' の入力を加えたとみなすことができます.
= Rs/(Rs + Rf) の負帰還増幅器に,
ei' の入力を加えたとみなすことができます.