next up previous
Next: 7 シミュレーション Up: P-G帰還の謎を解く Previous: 5 P-G帰還回路の出力インピーダンス

6 等価回路による解析

P-G帰還の等価回路は、図4のようになります。
図 4: P-G帰還の等価回路
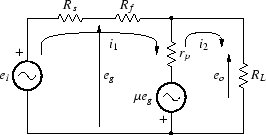
\begin{figure}\input{figs/pg_equiv} \end{figure}

これより、次の関係が成り立ちます。

ei + $\displaystyle \mu$eg = i1(Rs + Rf) + (i1 - i2)rp (13)
- $\displaystyle \mu$eg = (i2 - i1)rp + i2RL (14)
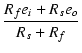eg = $\displaystyle {\frac{{R_f e_i + R_s e_o}}{{R_s + R_f}}}$ (15)
eo = i2RL (16)

6.1 ゲイン

式(16)より、

i2 = $\displaystyle {\frac{{e_o}}{{R_L}}}$ (17)
この式と式(15)を 式(13), (14)に代入して、
ei + $\displaystyle \mu$$\displaystyle {\frac{{R_f e_i + R_s e_o}}{{R_s + R_f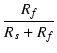}}}$ = i1(rp + Rs + Rf) - 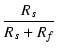$\displaystyle {\frac{{r_p}}{{R_L}}}$eo  
$\displaystyle \Bigl($1 + $\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{R_s + R_f}}}$$\displaystyle \Bigr)$ei = i1(rp + Rs + Rf) - $\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$ + $\displaystyle {\frac{{r_p}}{{R_L}}}$$\displaystyle \Bigr)$eo (18)
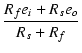- $\displaystyle \mu$$\displaystyle {\frac{{R_f e_i + R_s e_o}}{{R_s + R_f}}}$ = - i1rp + $\displaystyle {\frac{{e_o}}{{R_L}}}$(rp + RL)  
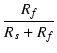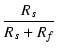i1rp = $\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{R_s + R_f}}}$ei + $\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$ + $\displaystyle {\frac{{r_p}}{{R_L}}}$ +1$\displaystyle \Bigr)$eo  
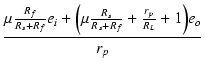i1 = $\displaystyle {\frac{{\mu \frac{R_f}{R_s + R_f} e_i + \Bigl( \mu \frac{R_s}{R_s + R_f} + \frac{r_p}{R_L} + 1 \Bigr) e_o}}{{r_p}}}$ (19)

式(19)を式(18)に代入して、
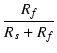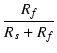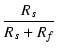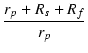$\displaystyle \Bigl($1 + $\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{R_s + R_f}}}$$\displaystyle \Bigr)$ei = $\displaystyle \Bigl\{$$\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{R_s + R_f}}}$ei + $\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$ + $\displaystyle {\frac{{r_p}}{{R_L}}}$ +1$\displaystyle \Bigr)$eo$\displaystyle \Bigr\}$$\displaystyle {\frac{{r_p + R_s + R_f}}{{r_p}}}$  
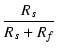      - $\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$ + $\displaystyle {\frac{{r_p}}{{R_L}}}$$\displaystyle \Bigr)$eo  
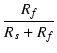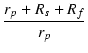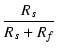$\displaystyle \Bigl\{$1 + $\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{R_s + R_f}}}$$\displaystyle \Bigl($1 - $\displaystyle {\frac{{r_p + R_s + R_f}}{{r_p}}}$$\displaystyle \Bigr)$$\displaystyle \Bigr\}$ei = $\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$ + $\displaystyle {\frac{{r_p}}{{R_L}}}$$\displaystyle \Bigr)$$\displaystyle \Bigl($$\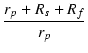displaystyle {\frac{{r_p + R_s + R_f}}{{r_p}}}$ -1$\displaystyle \Bigr)$ + $\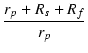displaystyle {\frac{{r_p + R_s + R_f}}{{r_p}}}$$\displaystyle \Bigr\}$eo  
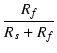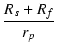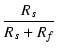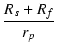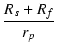$\displaystyle \Bigl($1 - $\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{R_s + R_f}}}$ . $\displaystyle {\frac{{R_s + R_f}}{{r_p}}}$$\displaystyle \Bigr)$ei = $\displaystyle \Bigl\{$$\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$ + $\displaystyle {\frac{{r_p}}{{R_L}}}$$\displaystyle \Bigr)$$\displaystyle {\frac{{R_s + R_f}}{{r_p}}}$ + $\displaystyle {\frac{{R_s + R_f}}{{r_p}}}$ +1$\displaystyle \Bigr\}$eo  
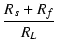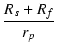$\displaystyle \Bigl($1 - $\displaystyle \mu$$\displaystyle {\frac{{R_f}}{{r_p}}}$$\displaystyle \Bigr)$ei = $\displaystyle \Bigl($$\displaystyle \mu$$\displaystyle {\frac{{R_s}}{{r_p}}}$ + $\displaystyle {\frac{{R_s + R_f}}{{R_L}}}$ + $\displaystyle {\frac{{R_s + R_f}}{{r_p}}}$ +1$\displaystyle \Bigr)$eo  
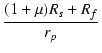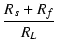  = $\displaystyle \Bigl\{$$\displaystyle {\frac{{(1 + \mu)R_s + R_f}}{{r_p}}}$ + $\displaystyle {\frac{{R_s + R_f}}{{R_L}}}$ +1$\displaystyle \Bigr\}$eo  
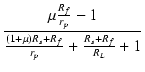eo = - $\displaystyle {\frac{{\mu \frac{R_f}{r_p} - 1}}{{\frac{(1 + \mu) R_s + R_f}{r_p} + \frac{R_s + R_f}{R_L} + 1 }}}$ei (20)
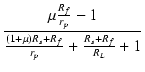Af = - $\displaystyle {\frac{{\mu \frac{R_f}{r_p} - 1}}{{\frac{(1 + \mu) R_s + R_f}{r_p} + \frac{R_s + R_f}{R_L} + 1 }}}$ (21)

6.2 入力インピーダンス

式(13)と式(14)を足し、 式(16)を代入すると、
ei = i1(Rs + Rf) + i2RL = i1(Rs + Rf) + eo  
i1 = $\displaystyle {\frac{{e_i - e_o}}{{R_s + R_f}}}$  

式(20)を代入すると、
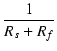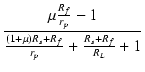i1 = $\displaystyle {\frac{{1}}{{R_s + R_f}}}$$\displaystyle \Bigl\{$1 + $\displaystyle {\frac{{\mu \frac{R_f}{r_p} - 1}}{{\frac{(1 + \mu) R_s + R_f}{r_p} + \frac{R_s + R_f}{R_L} + 1 }}}$$\displaystyle \Bigr\}$ei  
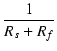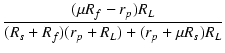  = $\displaystyle {\frac{{1}}{{R_s + R_f}}}$$\displaystyle \Bigl\{$1 + $\displaystyle {\frac{{(\mu R_f - r_p) R_L}}{{(R_s+R_f)(r_p+R_L) + (r_p + \mu R_s) R_L}}}$$\displaystyle \Bigr\}$ei  
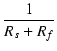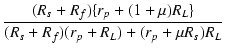  = $\displaystyle {\frac{{1}}{{R_s + R_f}}}$ . $\displaystyle {\frac{{(R_s+R_f)\{r_p + (1 + \mu)R_L\}}}{{(R_s+R_f)(r_p+R_L) + (r_p + \mu R_s) R_L}}}$ei  

これより、入力インピーダンス Zi は、
Zi = $\displaystyle {\frac{{e_i}}{{i_1}}}$  
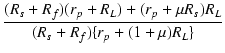  = (Rs + Rf)$\displaystyle {\frac{{(R_s+R_f)(r_p+R_L) + (r_p + \mu R_s) R_L}}{{(R_s+R_f)\{r_p + (1 + \mu)R_L\}}}}$  
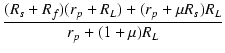  = $\displaystyle {\frac{{(R_s+R_f)(r_p+R_L) + (r_p + \mu R_s )R_L}}{{r_p + (1 + \mu)R_L}}}$ (22)

6.3 出力インピーダンス

出力インピーダンスを求めるための等価回路は、 図5のようになります。
図 5: P-G帰還の出力インピーダンスを求めるための等価回路
\begin{figure}\input{figs/pg_zo_equiv} \end{figure}

これより、以下の関係が成り立ちます。

i1 = $\displaystyle {\frac{{e}}{{R_s + R_f}}}$ (23)
i2 = $\displaystyle {\frac{{\mu e_g + e}}{{r_p}}}$ (24)
i3 = $\displaystyle {\frac{{e}}{{R_L}}}$ (25)
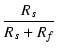eg = $\displaystyle {\frac{{R_s}}{{R_s+R_f}}}$e (26)

これより、
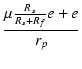i2 = $\displaystyle {\frac{{\mu \frac{R_s}{R_s + R_f} e + e}}{{r_p}}}$  
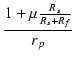  = $\displaystyle {\frac{{1 + \mu\frac{R_s}{R_s + R_f}}}{{r_p}}}$e (27)

したがって、出力インピーダンス Zo は、
Zo = $\displaystyle {\frac{{e}}{{i_1 + i_2 + i_3}}}$  
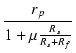  = (Rs + Rf)//RL//$\displaystyle {\frac{{r_p}}{{1 + \mu\frac{R_s}{R_s + R_f}}}}$ (28)

next up previous
Next: 7 シミュレーション Up: P-G帰還の謎を解く Previous: 5 P-G帰還回路の出力インピーダンス
Ayumi Nakabayashi
平成19年12月3日