Next: 3.3 カソード帰還の内部抵抗 Up: 3. 出力段の局部帰還(ウルトラリニアとカソード帰還) Previous: 3.1 UL接続のプレート特性
|
rp = |
(3.6) |
|
rp = |
(3.7) |
一次巻線に対するSGタップの比率を
![]() とします.
この場合,プレート電圧が
とします.
この場合,プレート電圧が
![]() Ep
上昇すると,
スクリーングリッド(G2)の電圧は,
Ep
上昇すると,
スクリーングリッド(G2)の電圧は,
![]()
![]() Ep
上昇します.
Ep
上昇します.
![]() を一般的な値である0.43とし,
を一般的な値である0.43とし,
![]() Ep = 10 V
とすれば,G2は
0.43 x 10 = 4.3 V
上昇します.
Ep = 10 V
とすれば,G2は
0.43 x 10 = 4.3 V
上昇します.
G2の電圧が 1 V
上がることは,
コントロールグリッド(G1)の電圧が
1/μg1-g2 V
上がることと等価です.
ここで,
μg1-g2
は,G1-G2間の増幅率です3.1.
したがって,プレート電圧が
![]() Ep
上がったときのプレート電圧とプレート電流の関係は,
グリッド電圧が
Ep
上がったときのプレート電圧とプレート電流の関係は,
グリッド電圧が
![]()
![]() Ep/μg1-g2
上がった特性曲線で表されます.
この例の場合,
μg1-g2 = 7.73
ですので,等価的なグリッド電圧の上昇分
Ep/μg1-g2
上がった特性曲線で表されます.
この例の場合,
μg1-g2 = 7.73
ですので,等価的なグリッド電圧の上昇分
![]() Eg
は,
Eg
は,
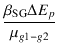 = = 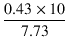 = 0.556 [V] = 0.556 [V]
|
(3.8) |
これより,UL接続の場合,プレート電圧が
![]() Ep
上昇したとき,
プレート電流は,
Ep
上昇したとき,
プレート電流は,
したがって,UL接続時の内部抵抗
rp(UL)
は,
|
rp(UL) |
(3.12) |
rp(UL) = 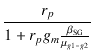 = = 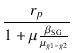
|
(3.13) |
図の例の場合, gm = 3.873 mS なので,式(3.9)より,
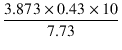 = 2.332 [mA] = 2.332 [mA]
|
(3.14) |
|
rp(UL) = |
(3.15) |
ここまでの計算では,スクリーングリッド電流の寄与分を考えていませんでしたが,
これを考慮するには,gm
の代わりに
gm(UL) = gm(1 + ![]() Ig20/Ip0)
を使います.
Ig20/Ip0)
を使います.
rp(UL) = 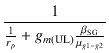
|
(3.16) |
ayumi