Next: 3.4 等価回路による解析 Up: 3. 出力段の局部帰還(ウルトラリニアとカソード帰還) Previous: 3.2 UL接続のプレート内部抵抗
三極管シングルの出力段にカソード帰還をかけた場合の回路を図3.8に示します.
カソード-プレート間の巻数に対する,カソード帰還巻線の割合を
![]() とします.
とします.
内部抵抗を求めるため,仮にカソード-プレート間の電圧が
![]() Ep
だけ上昇したと仮定します.
このとき,カソード帰還巻線には
Ep
だけ上昇したと仮定します.
このとき,カソード帰還巻線には
![]()
![]() Ep
の電圧が生じ,
アースを基準とすると,カソードの電位は
Ep
の電圧が生じ,
アースを基準とすると,カソードの電位は
![]()
![]() Ep
下がります.
これはグリッドに
Ep
下がります.
これはグリッドに
![]()
![]() Ep
の入力が加えられたことと同じですから,
プレート電流は,
gm
Ep
の入力が加えられたことと同じですから,
プレート電流は,
gm![]()
![]() Ep
増えます.
また,真空管の内部抵抗により,グリッド電圧が変わらなくても
Ep
増えます.
また,真空管の内部抵抗により,グリッド電圧が変わらなくても
![]() Ep/rp
だけプレート電流が増えます.
したがって,プレート電流の総増分
Ep/rp
だけプレート電流が増えます.
したがって,プレート電流の総増分
![]() Ip(KF)
は,
Ip(KF)
は,
|
|
(3.17) |
|
rp(KF) = rp// |
(3.19) |
さきほどと同じ6L6-GCの例で見てみましょう.
プレート特性図を図3.9に示します.
負荷インピーダンスは
5 kΩ
とし,
16 Ω
の巻線でカソード帰還をかけることにします.
巻数比は
![]() :
: ![]() = 17.68
ですから,
= 17.68
ですから,
![]() = 1/(17.68 + 1) = 0.05354
となります.
= 1/(17.68 + 1) = 0.05354
となります.
プレート電圧の変化を
![]() Ep = 10 V
とすると,
カソード帰還巻線に生じる電圧は,
Ep = 10 V
とすると,
カソード帰還巻線に生じる電圧は,
![]()
![]() Ep = 0.05354 x 10 = 0.5354 V
で,これがグリッドに加えられます.
これによるプレート電流の増分ACは,
gm = 3.873 mS
なので,
gm
Ep = 0.05354 x 10 = 0.5354 V
で,これがグリッドに加えられます.
これによるプレート電流の増分ACは,
gm = 3.873 mS
なので,
gm![]() Eg = 3.873 x 0.5354 = 2.07 mA
となり,
内部抵抗
rp(KF)
は,
Eg = 3.873 x 0.5354 = 2.07 mA
となり,
内部抵抗
rp(KF)
は,
rp(KF) = 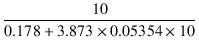 = 4.44 [kΩ] = 4.44 [kΩ]
|
(3.20) |
式(3.18)から求めると, rp = 56.2 kΩ , gm = 3.873 mS より, μ = 217.7 ですから,
rp(KF) = 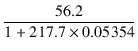 = 4.44 [kΩ] = 4.44 [kΩ]
|
(3.21) |
ここで6L6-GCの数値例を示しましたが, 多極管の場合,実際にはアースに対してカソードの電位が変動する一方, スクリーングリッドの電圧は一定なので, カソードを基準とするとスクリーングリッドの電圧が変動することになり, ごく弱いUL接続になっていることがわかります. ここでは,この影響を無視しています.
ayumi