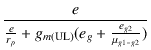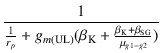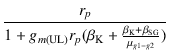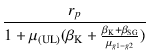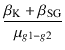UL接続とカソード帰還は,同時に解析することができます.
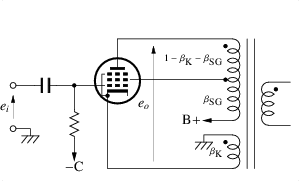
図3.10の回路を考えます.
プレート-カソード間の巻数を1としたときの,
SGタップの割合を
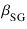 ,
カソード帰還巻線の割合を
,
カソード帰還巻線の割合を
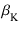 とします.
とします.
図 3.10:
UL接続とカソード帰還を同時に使用した回路
 |
ゲインを求める等価回路は,図3.11のようになります.
等価回路より,次の関係が成り立ちます.
| eg |
= |
ei + 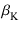 eo eo |
(3.22) |
| eg2 |
= |
(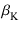 + + 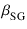 )eo )eo |
(3.23) |
| eo |
= |
- gm(UL)(eg + 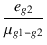 )(rp//RL) )(rp//RL) |
(3.24) |
これより,
| eo |
= |
- gm(UL)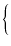 ei + ei + 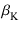 eo + eo + 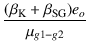 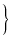 (rp//RL) (rp//RL) |
|
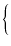 1 + gm(UL) 1 + gm(UL)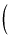 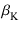 + + 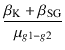  (rp//RL) (rp//RL) eo eo |
= |
- gm(UL)ei(rp//RL) |
|
| eo |
= |
- 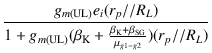 |
(3.25) |
| Af |
= |
- 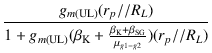 |
(3.26) |
帰還のない時のゲイン A
は,
|
A = gm(UL)(rp//RL)
|
(3.27) |
ですから,帰還後のゲインは,
Af = - 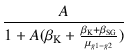
|
(3.28) |
と表すことができ,帰還量 F
は,
となります.
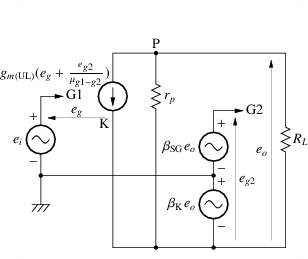
図 3.11:
UL接続とカソード帰還のゲインを求める等価回路
 |
内部抵抗を求めるには,等価回路を書いて,
グリッドをアースに落とし,
プレート-カソード間に電圧 e
を加え,
流れ込んだ電流 i
の大きさを求め,rp' = e/i
で求めます.
等価回路は,図3.12のようになります.
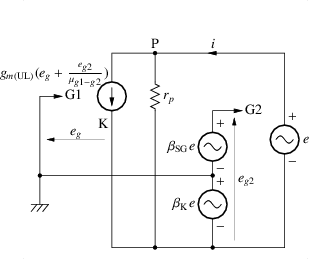
図 3.12:
UL接続とカソード帰還の内部抵抗を求める等価回路
 |
プレート-カソード間に電圧 e
を加えると,
SGタップには
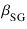 e
の電圧が,
カソード帰還巻線には
e
の電圧が,
カソード帰還巻線には
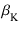 e
の電圧が発生します.
カソードを基準にすると,
コントロールグリッドには,カソード帰還巻線の電圧がかかり,
スクリーングリッドには, カソード帰還巻線とSGタップの電圧を加えたものがかかります.
スクリーングリッドに生じた電圧 eg2
は,コントロールグリッドに換算すれば
1/μg1-g2
倍となります.
これらより,次の関係が成り立つことがわかります.
e
の電圧が発生します.
カソードを基準にすると,
コントロールグリッドには,カソード帰還巻線の電圧がかかり,
スクリーングリッドには, カソード帰還巻線とSGタップの電圧を加えたものがかかります.
スクリーングリッドに生じた電圧 eg2
は,コントロールグリッドに換算すれば
1/μg1-g2
倍となります.
これらより,次の関係が成り立つことがわかります.
| eg |
= |
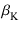 e e |
(3.30) |
| eg2 |
= |
(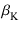 + + 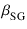 )e )e |
(3.31) |
| i |
= |
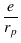 + gm(UL)(eg + + gm(UL)(eg + 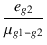 ) ) |
(3.32) |
したがって,UL接続とカソード帰還をかけた場合の等価内部抵抗 rp'
は,
となり,式(3.10)や式(3.18)と同じであることがわかります.
この式は,
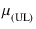 = gm(UL)rp =
= gm(UL)rp = 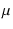 (1 +
(1 + 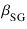 Ig20/Ip0)
とおけば,
Ig20/Ip0)
とおけば,
| rp' |
= |
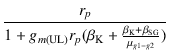 |
|
| |
= |
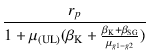 |
(3.34) |
と変形でき,内部抵抗の減少率 F'
は,
となります.帰還量 F
の式では A
であったところが 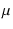 になっていることに注意してください.
この F'
は,負荷を掛けない状態における(真の)帰還量でもあります.
になっていることに注意してください.
この F'
は,負荷を掛けない状態における(真の)帰還量でもあります.
ayumi
2016-03-07
![]() ,
カソード帰還巻線の割合を
,
カソード帰還巻線の割合を
![]() とします.
とします.
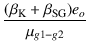
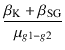
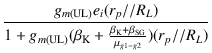
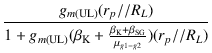
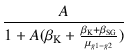
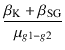
![]() e
の電圧が,
カソード帰還巻線には
e
の電圧が,
カソード帰還巻線には
![]() e
の電圧が発生します.
カソードを基準にすると,
コントロールグリッドには,カソード帰還巻線の電圧がかかり,
スクリーングリッドには, カソード帰還巻線とSGタップの電圧を加えたものがかかります.
スクリーングリッドに生じた電圧 eg2
は,コントロールグリッドに換算すれば
1/μg1-g2
倍となります.
これらより,次の関係が成り立つことがわかります.
e
の電圧が発生します.
カソードを基準にすると,
コントロールグリッドには,カソード帰還巻線の電圧がかかり,
スクリーングリッドには, カソード帰還巻線とSGタップの電圧を加えたものがかかります.
スクリーングリッドに生じた電圧 eg2
は,コントロールグリッドに換算すれば
1/μg1-g2
倍となります.
これらより,次の関係が成り立つことがわかります.