Next: 3.6 実例 Up: 3. 出力段の局部帰還(ウルトラリニアとカソード帰還) Previous: 3.4 等価回路による解析
この節では,6L6-GCを例に, 各種接続のゲインと内部抵抗を求めます. 動作点は, Ep0 = 250 V , Eg0 = - 20 V , Eg20 = 250 V , Ip0 = 36.92 mA , Ig20 = 2.564 mA で, この動作点における三定数は, μ = 216.8 , gm = 3.873 mS , rp = 56.0 kΩ です. 負荷は RL = 5 kΩ とします.
本来,この動作点では, ロードラインがニーポイントを通るように負荷を低くとって, より大きな出力が得られるようにすべきです. ここでは,UL動作に向くよう負荷を 5 kΩ としています. そのため,フルスイングする前に特性曲線が曲がっている部分にかかってしまいます. ここでは,最低プレート電圧が50Vとなるまで入力を加えていますが, これ以上入力を加えても,歪みが増えるだけです. プレート電圧が250Vで,負荷が 5 kΩ の場合は, スクリーングリッド電圧を下げ,バイアスを浅くしても出力は減りません.
簡易的に計算した出力は,
| Po = (380.2 - 50.0) x (0.0769 - 0.0109)/8 = 2.72 [W] | (3.36) |
シミュレーションの回路図を図3.14に, 各部の波形を図3.15に示します.
等価回路によるゲインと出力インピーダンスは,
| A | = | - gm(rp//RL) = - 3.873 x (56.0//5) = - 17.8 | (3.37) |
| Zo | = | 56.0 [kΩ] | (3.38) |
シミュレーションの回路図を図3.17に, 各部の波形を図3.18に示します.
簡易的に計算した出力は,
| Po = (378.7 - 50.0) x (0.078 - 0.0123)/8 = 2.70 [W] | (3.39) |
等価回路によるゲインと出力インピーダンスは,
| gm(UL) | = | gm(1 + 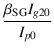 ) = 3.873 x (1 + ) = 3.873 x (1 + 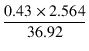 ) = 3.99 [mS] ) = 3.99 [mS] |
(3.40) |
| = | 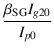 ) = 216.8 x (1 + ) = 216.8 x (1 + 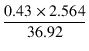 ) = 223.3 ) = 223.3 |
(3.41) | |
| A | = | - gm(UL)(rp//RL) = - 3.99 x (56.0//5) = - 18.31 | (3.42) |
| F | = | 1 + | A| |
(3.43) |
| Af | = | - |
(3.44) |
| F' | = | 1 + |
(3.45) |
| Zo | = | (3.46) |
シミュレーションの回路図を図3.20に, 各部の波形を図3.21に示します.
簡易的に計算した出力は,
| Po = (345.5 - 115.2) x (0.0664 - 0.0204)/8 = 1.32 [W] | (3.47) |
等価回路によるゲインと出力インピーダンスは,
| gm(UL) | = | gm(1 + |
(3.48) |
| = | (3.49) | ||
| A | = | - gm(UL)(rp//RL) = - 4.14 x (56.0//5) = - 19.0 | (3.50) |
| F | = | 1 + | A| |
(3.51) |
| Af | = | - |
(3.52) |
| F' | = | 1 + |
(3.53) |
| Zo | = | (3.54) |
プレート-電源間の負荷を 5 kΩ ,カソード帰還巻線を 16 Ω とします. プレート-カソード間は一次巻線と二次巻線が直列になり, 真空管の負荷インピーダンスは定格一次インピーダンスとは違ってきます. まず,このインピーダンスを求めます.
一次の巻数を n1 , 二次の巻数を n2 とします. 定格一次インピーダンスを Zp , 二次インピーダンスを Zs とすると,
となります. カソード帰還時のプレート-カソード間負荷インピーダンスを ZpKF とすると, この式に式(3.55)を代入して,| = | |||
| ZpKF | = | Zs |
|
| = | ( |
(3.57) |
この例では
Zp = 5000 Ω
,
Zs = 16 Ω
で,
巻数比は
![]() :
: ![]() = 17.68
ですから,
= 17.68
ですから,
![]() = 1/(17.68 + 1) = 0.05354
となります.
プレート-カソード間の負荷は
ZpKF = (
= 1/(17.68 + 1) = 0.05354
となります.
プレート-カソード間の負荷は
ZpKF = (![]() +
+ ![]() )2 = 5582 Ω
です.
)2 = 5582 Ω
です.
プレート特性図は,図3.22のようになります.
図中の緑色のカーブは,多極管接続のプレート特性で, 赤いカーブが5.354%タップのUL接続のプレート特性です. 両者は少し異なっていますが,UL接続のプレート特性を描くのが面倒な時は, 多極管接続のプレート特性を使っても大差ないことがわかります. 青色の直線が 5582 Ω のロードラインです.この動作点と負荷は,多極管接続に最適ではありません. 本来は正味(グリッド-カソード間)のグリッド電圧が0になるまで入力を加えますが, ここでは正味のプレート電圧が 50V になるまで入力を加えることにします. この例の場合,グリッド電圧が -9.58 V になるとプレート電圧が 50V になります. このとき,プレート電圧は動作点より 200V 下がるので, カソードの電圧は 200 x 0.05354 = 10.708 V に上昇します. したがって,入力電圧の尖頭値は (20 - 9.58) + 10.708 = 21.128 V になります.
入力信号の負のピークでは,プレート電圧が 407Vまで上昇し, このときカソードの電圧は (250 - 407) x 0.05354 = - 8.406 V となり, 正味のグリッド電圧は, -20 - 21.128 + 8.406 = - 32.72 V となります.
シミュレーションの回路図を図3.23に, 各部の波形を図3.24〜3.26に示します.
図3.24では,緑のカーブがプレート電流で, 青のカーブがスクリーングリッド電流です. 赤いカーブはスクリーングリッド電流が出力に寄与する分を加えた実効プレート電流です. カソード帰還では,カソード側の巻線にスクリーングリッド電流が流れるので,このように実効プレート電流を求める必要があります.
図3.25では,緑のカーブが対グラウンドのプレート電圧で, 赤のカーブがプレート-カソード間のいわゆるプレート電圧です.
図3.26の緑のカーブは対グラウンドのグリッド電圧で,青いカーブはカソードの電圧です. 緑から青を引いたものが正味のグリッド電圧で,赤いカーブで示しています.
簡易的に計算した出力は,
です. 標本化した信号とFFTによって算出した出力と歪率は,2.99W, 6.28%でした.
ゲインと出力インピーダンスは,
| gm(UL) | = | 3.873 x (1 + 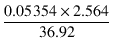 ) = 3.888 [mS] ) = 3.888 [mS] |
(3.59) |
| mu(UL) | = | 216.8 x (1 + 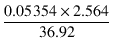 ) = 217.6 [mS] ) = 217.6 [mS] |
(3.60) |
| = | 0.05354 + 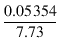 = 0.06047 = 0.06047 |
(3.61) | |
| A | = | -3.888 x (56.0//5.582) = - 19.73 | (3.62) |
| F | = | 1 + | A| |
(3.63) |
| Af | = | - |
(3.64) |
| F' | = | 1 + |
(3.65) |
| Zo | = | (3.66) |
カソード帰還の部分をブラックボックスとして, 入力端子とプレート端子があるデバイスと考えて, プレート特性を描いてみます. 回路は,図3.27です.
VG は動作点のバイアス電圧で,一定とします. VI は入力電圧で,これを -25 V から 25V まで変化させて, プレート電圧とプレート電流の関係を描きます. ARB1 はプレート電圧の静止時との差を検出して, その0.05656854倍をカソードに帰還する電圧源です. これはカソード巻線の代替で,直流でも動作するものです.
このようにして特性図を描くと,図3.28の実線のようになり, UL接続の特性図と似ていることがわかります.
この特性図に描くロードラインの値について検討します. カソード帰還では,UL接続と同様に,プレート電流に加え, スクリーングリッド電流がカソード帰還巻線に流れます. この様子を図3.29に示します.
一次巻線と二次巻線(カソード帰還巻線)で流れる電流が異なりますので,
UL接続の場合と同様に両者に同じ信号電流が流れるようにするためには,
信号電流を
ip + ![]() ig2
と考えます(b).
このとき,P-K間だけの,タップのない出力トランスとして扱うことができ,
このインピーダンスは,
(
ig2
と考えます(b).
このとき,P-K間だけの,タップのない出力トランスとして扱うことができ,
このインピーダンスは,
(![]() +
+ ![]() )2
です.
すなわち,
)2
です.
すなわち,
|
|
(3.67) |
ところで,図3.28では,x
軸は対グラウンドのプレート電圧ですから,図3.29 (b)の上側の四角を見ていることになります.
したがって,ロードラインのインピーダンス RL
は,
| RL | = | 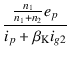 |
|
| = | |||
| = | |||
| = | 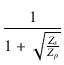 ( ( |
||
| = | 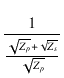 ( ( |
||
| = | 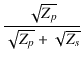 ( ( |
||
| = | |||
| = | Zp + |
(3.68) |
となります. 図3.28には,この値のロードラインを青い直線で引いています. また点線の特性は,スクリーングリッド電流の一部を加えたものです.
前節より,入力信号の尖頭値を 21.13V とすると, 点線の特性図とロードラインの交点は図で示した電圧・電流となります. 出力を求めるには,電圧を全巻線に換算する必要があります. この係数は
です. したがって出力は,
(398.6 - 60.7) x (1 + 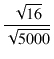 ) x (0.0729 - 0.0089)/8 = 2.86 [W] ) x (0.0729 - 0.0089)/8 = 2.86 [W]
|
(3.69) |
ayumi