next up previous
Next: 4. プッシュプル出力段 Up: 3. 出力段の局部帰還(ウルトラリニアとカソード帰還) Previous: 3.5 数値例とシミュレーション

Subsections

3.6 実例

6L6と同特性の5881を用いたシングルアンプで動作を検証します． 電源は定電圧電源を使用し，出力トランスの電源側が 250V になるようにします． したがって，プレート電圧は，出力トランスの巻線抵抗によるドロップ分だけ低くなります． 電圧増幅段は，5751による差動増幅回路です． 回路の詳細は，6CK4による各種出力段の比較実験を参照してください．

3.6.1 トランスの特性

使用するトランスは，TANGOのU-7083.2，東栄変成器のOPT-10S です． 各トランスの仕様は，以下の通りです．
U-708 OPT-10S
一次巻線抵抗 r1 (Ω ) 195.4 263.7
二次巻線抵抗 r2 (Ω ) 0.43 0.72
巻数比 23.85 23.92
一次インピーダンス(Ω ) 4991 5253
KNF時一次インピーダンス Za (Ω ) 5574 5642
KNF時P-Bインピーダンス Zp (Ω ) 5271 5443
SGタップ比率(%) 37.4 39.9
KNF比率 $ \beta$ (%) 5.43 3.53

SGタップ比率やカソード帰還用巻線のインピーダンスが異なっているので， 特に出力インピーダンスの違いが現れてくることが期待できます．

基本的にはU-708の結果を紹介し， トランスによって大きく違いがある場合は，他のトランスの結果も記載します．

3.6.1.1 巻線抵抗がある場合のKNF接続一次インピーダンス

ここで，巻線抵抗がある場合の，プレート-グラウンド間のインピーダンスおよび， KNFの帰還率 $ \beta$ を求める方法を考えます． 等価回路は，図3.31のようになります．
図 3.31: 巻線抵抗がある場合のKNF接続の等価回路
\begin{figure}\input{figs/knf_tr1} \end{figure}
ここで，
ip = プレート電流  
ig2 = スクリーングリッド電流  
r1 = 一次巻線抵抗  
r2 = 二次巻線抵抗  
r3 = 3次(KNF)巻線抵抗  
RL = 負荷抵抗(二次に接続)  
n1 = 一次巻数  
n2 = 二次巻数  
n3 = 3次(KNF)巻数  
e1 = 巻線抵抗を除いた一次の電圧  
e2 = 巻線抵抗を除いた二次の電圧  
e3 = 巻線抵抗を除いた3次の電圧  
e13 = 巻線抵抗を除いたP-K間電圧  
ep = 一次の電圧  
et = 3次の電圧  

とすると，等価回路より， 一次巻線と二次巻線のアンペアターンが等しいことから，

ipn1 + (ip + ig2)n3 = i2n2 (3.70)
巻数比と電圧の関係から，
e1 = $\displaystyle {\frac{{n_1}}{{n_2}}}$e2  
e3 = $\displaystyle {\frac{{n_3}}{{n_2}}}$e2  

二次に生じる電圧と負荷抵抗の関係から，

e2 = i2(r2 + RL) (3.71)
式(3.70)より，
i2n2 = ip(n1 + n3) + ig2n3  
i2 = ip$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$ + ig2$\displaystyle {\frac{{n_3}}{{n_2}}}$  
  = ip$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$ + ig2$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$ . $\displaystyle {\frac{{n_3}}{{n_1 + n_3}}}$  
  = $\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$$\displaystyle \Bigl($ip + $\displaystyle {\frac{{n_3}}{{n_1 + n_3}}}$ig2$\displaystyle \Bigr)$  

ここで， $ \beta{^\prime}$ = n3/(n1 + n3) , ip' = ip + $ \beta{^\prime}$ig2 とおくと，

i2 = $\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$ip'

これを式(3.71)に代入して，
e2 = $\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$ip'(r2 + RL)  
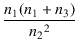e1 = $\displaystyle {\frac{{n_1}}{{n_2}}}$e2 = $\displaystyle {\frac{{n_1(n_1 + n_3)}}{{{n_2}^2}}}$ip'(r2 + RL)  
e3 = 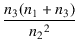$\displaystyle {\frac{{n_3}}{{n_2}}}$e2 = $\displaystyle {\frac{{n_3(n_1 + n_3)}}{{{n_2}^2}}}$ip'(r2 + RL)  

プレート特性に引くロードラインのインピーダンスを求めます． プレート特性上の電流は，ip' に相当します． この電流が流れたときに巻線抵抗を含む一次側に生じる電圧 ea は， ig2 = $ \alpha$ip とおくと， ip = ip'/(1 + $ \alpha$$ \beta{^\prime}$) , ig2 = $ \alpha$ip'/(1 + $ \alpha$$ \beta{^\prime}$) より，

ea = ipr1 + (ip + ig2)r3 + e1 + e3  
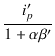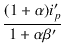  = $\displaystyle {\frac{{i_p'}}{{1 + \alpha \beta'}}}$r1 + $\displaystyle {\frac{{(1 + \alpha) i_p'}}{{1 + \alpha \beta'}}}$r3 + $\displaystyle \Bigl($$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$$\displaystyle \Bigr)^{2}_{}$ip'(r2 + RL)  
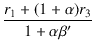  = $\displaystyle \Bigl\{$$\displaystyle {\frac{{r_1 + (1 + \alpha) r_3}}{{1 + \alpha \beta'}}}$ + $\displaystyle \Bigl($$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$$\displaystyle \Bigr)^{2}_{}$(r2 + RL)$\displaystyle \Bigr\}$ip'  
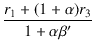Za = $\displaystyle {\frac{{r_1 + (1 + \alpha) r_3}}{{1 + \alpha \beta'}}}$ + $\displaystyle \Bigl($$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$$\displaystyle \Bigr)^{2}_{}$(r2 + RL)  

図3.28のようなカソード帰還の特性図に引くロードラインのインピーダンス Zp を求めます． この特性図の電流は，やはり ip' であり， この電流が流れたときに巻線抵抗を含む一次側に生じる電圧 ep は，

ep = ipr1 + e1  
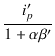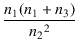  = $\displaystyle {\frac{{i_p'}}{{1 + \alpha \beta'}}}$r1 + $\displaystyle {\frac{{n_1(n_1 + n_3)}}{{{n_2}^2}}}$ip'(r2 + RL)  
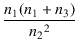  = $\displaystyle \Bigl\{$$\displaystyle {\frac{{r_1}}{{1 + \alpha \beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_3)}}{{{n_2}^2}}}$(r2 + RL)$\displaystyle \Bigr\}$ip'  
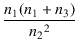Zp = $\displaystyle {\frac{{r_1}}{{1 + \alpha \beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_3)}}{{{n_2}^2}}}$(r2 + RL)  

同様にして，カソードに帰還される電圧は et は，

et = (ip + ig2)r3 + e3  
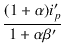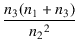  = $\displaystyle {\frac{{(1 + \alpha) i_p'}}{{1 + \alpha \beta'}}}$r3 + $\displaystyle {\frac{{n_3(n_1 + n_3)}}{{{n_2}^2}}}$ip'(r2 + RL)  
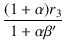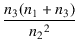  = $\displaystyle \Bigl\{$$\displaystyle {\frac{{(1 + \alpha) r_3}}{{1 + \alpha \beta'}}}$ + $\displaystyle {\frac{{n_3(n_1 + n_3)}}{{{n_2}^2}}}$(r2 + RL)$\displaystyle \Bigr\}$ip'  
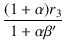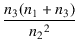Zt = $\displaystyle {\frac{{(1 + \alpha) r_3}}{{1 + \alpha \beta'}}}$ + $\displaystyle {\frac{{n_3(n_1 + n_3)}}{{{n_2}^2}}}$(r2 + RL)  

となるので， P-K間の電圧に対する帰還率 $ \beta$ は，
$\displaystyle \beta$ = $\displaystyle {\frac{{e_t}}{{e_a}}}$ = $\displaystyle {\frac{{Z_t}}{{Z_a}}}$  
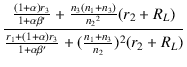  = $\displaystyle {\frac{{\frac{(1 + \alpha) r_3}{1 + \alpha \beta'} + \frac{n_3(n_... ...(1 + \alpha) r_3}{1 + \alpha \beta'} + (\frac{n_1 + n_3}{n_2})^2 (r_2 + R_L)}}}$  
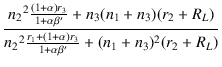  = $\displaystyle {\frac{{{n_2}^2 \frac{(1 + \alpha) r_3}{1 + \alpha \beta'} + n_3(... ...\frac{r_1 + (1 + \alpha) r_3}{1 + \alpha \beta'} + (n_1 + n_3)^2 (r_2 + R_L)}}}$  

となります．

U-708の場合， r1 = 195.4 , r2 = 0.43 , r3 = 5.84 , n1 = 2.669 , n2 = 0.1119 , n3 = 0.156 で， $ \alpha$ = 2.564/36.92 = 0.06944 ですから，

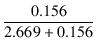$\displaystyle \beta{^\prime}$ = $\displaystyle {\frac{{n_3}}{{n_1 + n_3}}}$ = $\displaystyle {\frac{{0.156}}{{2.669+0.156}}}$ = 0.05522  
Za = 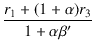$\displaystyle {\frac{{r_1 + (1 + \alpha) r_3}}{{1 + \alpha \beta'}}}$ + $\displaystyle \Bigl($$\displaystyle {\frac{{n_1 + n_3}}{{n_2}}}$$\displaystyle \Bigr)^{2}_{}$(r2 + RL)  
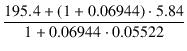  = $\displaystyle {\frac{{195.4 + (1 + 0.06944) \cdot 5.84}}{{1 + 0.06944 \cdot 0.05522}}}$ + $\displaystyle \Bigl($$\displaystyle {\frac{{2.669 + 0.156}}{{0.1119}}}$$\displaystyle \Bigr)^{2}_{}$(0.43 + 8) = 5573.7 [Ω]  
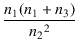Zp = $\displaystyle {\frac{{r_1}}{{1 + \alpha \beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_3)}}{{{n_2}^2}}}$(r2 + RL)  
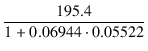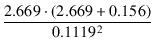  = $\displaystyle {\frac{{195.4}}{{1 + 0.06944 \cdot 0.05522}}}$ + $\displaystyle {\frac{{2.669 \cdot (2.669 + 0.156)}}{{0.1119^2}}}$(0.43 + 8) = 5270.8 [Ω]  
Zt = 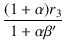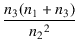$\displaystyle {\frac{{(1 + \alpha) r_3}}{{1 + \alpha \beta'}}}$ + $\displaystyle {\frac{{n_3(n_1 + n_3)}}{{{n_2}^2}}}$(r2 + RL)  
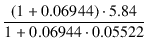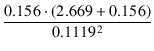  = $\displaystyle {\frac{{(1 + 0.06944) \cdot 5.84}}{{1 + 0.06944 \cdot 0.05522}}}$ + $\displaystyle {\frac{{0.156 \cdot (2.669 + 0.156)}}{{0.1119^2}}}$(0.43 + 8) = 302.92 [Ω]  
$\displaystyle \beta$ = $\displaystyle {\frac{{Z_t}}{{Z_a}}}$ = 0.05435  

となります．

3.6.1.2 巻線抵抗がある場合のオートトランスのインピーダンス

出力トランスにカソード帰還の専用巻線がないときに， カソード帰還をかけるには二次巻線で代用しますが， その場合のインピーダンスの計算は，専用巻線の場合と多少異なります． 等価回路は，図3.32のようになります．

図 3.32: 巻線抵抗がある場合のオートトランス接続の等価回路
\begin{figure}\input{figs/knf_tr2} \end{figure}
二次巻線を2つに分割し，入力側(カソード側)と出力側に分離します． ここで，
r1 = 一次巻線抵抗  
r2 = 二次巻線抵抗  
RL = 負荷抵抗  
n1 = 一次巻数  
n2 = 二次巻数  
i2 = 二次電流  

とすると， 等価回路より，一次巻線と二次巻線のアンペアターンが等しいことから，

ipn1 + (ip + ig2)n2 = i2n2 (3.72)
巻数比と電圧の関係から，

e1 = $\displaystyle {\frac{{n_1}}{{n_2}}}$e2

二次に生じる電圧と負荷抵抗の関係から，

e2 = (i2 - ip - ig2)r2 + i2RL (3.73)
式(3.72)より，
i2n2 = ip(n1 + n2) + ig2n2  
i2 = ip$\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$ + ig2  
  = $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$$\displaystyle \Bigl($ip + $\displaystyle {\frac{{n_2}}{{n_1 + n_2}}}$ig2$\displaystyle \Bigr)$  

ここで， $ \beta{^\prime}$ = n2/(n1 + n2) , ip' = ip + $ \beta{^\prime}$ig2 とおくと，

i2 = $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$ip' = $\displaystyle {\frac{{i_p'}}{{\beta'}}}$

これを式(3.73)に代入して，
e2 = 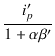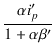$\displaystyle \Bigl($$\displaystyle {\frac{{i_p'}}{{\beta'}}}$ - $\displaystyle {\frac{{i_p'}}{{1 + \alpha \beta'}}}$ - $\displaystyle {\frac{{\alpha i_p'}}{{1 + \alpha\beta'}}}$$\displaystyle \Bigr)$r2 + $\displaystyle {\frac{{i_p'}}{{\beta'}}}$RL  
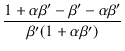  = $\displaystyle {\frac{{1 + \alpha\beta' - \beta' - \alpha\beta'}}{{\beta' (1 + \alpha\beta')}}}$ip'r2 + $\displaystyle {\frac{{i_p'}}{{\beta'}}}$RL  
  = $\displaystyle {\frac{{1 - \beta'}}{{\beta'}}}$ . $\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ip' + $\displaystyle {\frac{{R_L}}{{\beta'}}}$ip'  
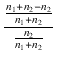  = $\displaystyle {\frac{{\frac{n_1 + n_2 - n_2}{n_1 + n_2}}}{{\frac{n_2}{n_1 + n_2}}}}$ . $\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ip' + $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RLip'  
  = $\displaystyle {\frac{{n_1}}{{n_2}}}$ . $\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ip' + $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RLip'  
  = $\displaystyle \Bigl($$\displaystyle {\frac{{n_1}}{{n_2}}}$ . $\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RL$\displaystyle \Bigr)$ip'  
e1 = $\displaystyle {\frac{{n_1}}{{n_2}}}$e2 = $\displaystyle {\frac{{n_1}}{{n_2}}}$$\displaystyle \Bigl($$\displaystyle {\frac{{n_1}}{{n_2}}}$ . $\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RL$\displaystyle \Bigr)$ip'  

プレート特性に引くロードラインのインピーダンスを求めます． プレート特性上の電流は，ip' に相当します． この電流が流れたときに巻線抵抗を含むPK間に生じる電圧 ea を求めますが， 最初に，一次に生じる電圧 ep と， 二次に生じる電圧 es を求めます．

ep = ipr1 + e1  
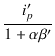  = $\displaystyle {\frac{{i_p'}}{{1 + \alpha \beta'}}}$r1 + $\displaystyle {\frac{{n_1}}{{n_2}}}$$\displaystyle \Bigl($$\displaystyle {\frac{{n_1}}{{n_2}}}$ . $\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RL$\displaystyle \Bigr)$ip'  
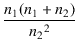  = $\displaystyle \Bigl\{$$\displaystyle {\frac{{r_1}}{{1 + \alpha \beta'}}}$ + $\displaystyle \Bigl($$\displaystyle {\frac{{n_1}}{{n_2}}}$$\displaystyle \Bigr)^{2}_{}$$\displaystyle {\frac{{r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_2)}}{{{n_2}^2}}}$RL$\displaystyle \Bigr\}$ip'  
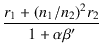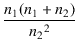  = $\displaystyle \Bigl\{$$\displaystyle {\frac{{r_1 + (n_1/n_2)^2 r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_2)}}{{{n_2}^2}}}$RL$\displaystyle \Bigr\}$ip'  
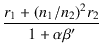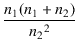Zp = $\displaystyle {\frac{{r_1 + (n_1/n_2)^2 r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_2)}}{{{n_2}^2}}}$RL  
es = (ip + ig2 - i2)r2 + e2  
  = - (i2 - ip - ig2)r2 + e2  

ここで，式(3.73)より， (i2 - ip - ig2)r2 = e2 - i2RL = e2 - ip'RL/$ \beta{^\prime}$ であるから，
es = - e2 + $\displaystyle {\frac{{i_p' R_L}}{{\beta'}}}$ + e2  
  = $\displaystyle {\frac{{R_L}}{{\beta'}}}$ip' = $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RLip'  
Zs = $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RL  

これより，プレート特性図に引くロードラインのインピーダンス Za は，

Za = Zp + Zs

P-K間の電圧に対する帰還率 $ \beta$ は，

$\displaystyle \beta$ = $\displaystyle {\frac{{e_s}}{{e_a}}}$ = $\displaystyle {\frac{{Z_s}}{{Z_a}}}$

となります．

OPT-10Sの場合， r1 = 263.7 , r2 = 0.72 , n1 = 2.672 , n2 = 0.1117 , $ \alpha$ = 0.06944 ですから，

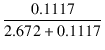$\displaystyle \beta{^\prime}$ = $\displaystyle {\frac{{n_2}}{{n_1 + n_2}}}$ = $\displaystyle {\frac{{0.1117}}{{2.672 + 0.1117}}}$ = 0.04013  
Zp = 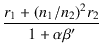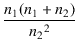$\displaystyle {\frac{{r_1 + (n_1/n_2)^2 r_2}}{{1 + \alpha\beta'}}}$ + $\displaystyle {\frac{{n_1(n_1 + n_2)}}{{{n_2}^2}}}$RL  
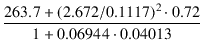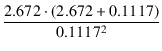  = $\displaystyle {\frac{{263.7 + (2.672/0.1117)^2 \cdot 0.72}}{{1 + 0.06944 \cdot 0.04013}}}$ + $\displaystyle {\frac{{2.672 \cdot (2.672 + 0.1117)}}{{0.1117^2}}}$ . 8 = 5443.0 [Ω]  
Zs = $\displaystyle {\frac{{n_1+n_2}}{{n_2}}}$RL  
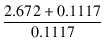  = $\displaystyle {\frac{{2.672 + 0.1117}}{{0.1117}}}$ . 8 = 199.4 [Ω]  
Za = Zp + Zs = 5443.0 + 199.4 = 5642.4 [Ω]  
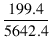$\displaystyle \beta$ = $\displaystyle {\frac{{Z_s}}{{Z_a}}}$ = $\displaystyle {\frac{{199.4}}{{5642.4}}}$ = 0.03533  

Zs の値が 8Ω 近辺ではありませんが， これは，一次側の電流と電圧でみたインピーダンスだからです．

3.6.2 多極管接続

シミュレーションによる各部の電圧・電流は， 図3.33のようになります． プレート電流が 36.75mA となるバイアスは， -20.01078 V でしたが，実際は -18.2 V でした． これ以降の実験では， バイアスを -18.2 V で固定します．

図 3.33: 多極管接続の回路(シミュレーション)
Image UL_6L6_U-708_pen_sch

モデルによるロードラインと伝達特性は， 図3.34のようになります．

図 3.34: 多極管接続プレートロードライン・伝達特性(U-708 シミュレーション)
\includegraphics[width=\linewidth]{figs/6L6_U-708_pen_lltsim.ps}
青い破線は，静止時のロードラインで， 入力に 9.25Vp の信号を加え続けると， 2次歪みにより下降した平均プレート電圧が元にもどるため， 動作点はO'に移動し，ロードラインは実線のようになります．

丸で示した点は，実機で観測された，オシロから読み取った値です． 特性曲線が，特にグリッド電圧が深いところでずれているようですが， おおむね合っているといえるでしょう． 下側の線はスクリーングリッド電流を表しています．

実機で観測されたロードラインと伝達特性を， 図3.35，3.36に示します． 各部の波形を， 図3.37，3.38に示します．

図 3.35: 多極管接続プレートロードライン・伝達特性(U-708)
Image 6L6_U-708_pen_llt
図 3.36: 多極管接続SGロードライン・伝達特性(U-708)
Image 6L6_U-708_pen_lltIg2
図 3.37: 多極管接続のプレート電流の波形(U-708)
Image 6L6_U-708_pen_Ip
図 3.38: 多極管接続のスクリーングリッド電流の波形(U-708)
Image 6L6_U-708_pen_Ig2

グリッド電圧が浅くなる Eg = - 15 V あたりから， 特にスクリーングリッド電流が急増しています． モデルでは，この増え方が多少ゆるやかになっているようです．

実際の出力トランスには巻線抵抗があるので， ダンピングファクターを計算するのは多少複雑になります． 今回の場合， rp = 55.664 kΩ で， 二次側から見た出力インピーダンス Zo は，

Zo = r2 + 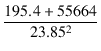$\displaystyle {\frac{{r_1 + r_p}}{{n^2}}}$ = 0.43 + $\displaystyle {\frac{{195.4 + 55664}}{{23.85^2}}}$ = 98.6 [Ω] (3.74)
となります． ここで，r1 は一次巻線抵抗，r2 は二次巻線抵抗，n は巻数比です． シミュレーションでは 80.7 Ω となりました． これくらい内部抵抗が高いと， 出力トランスの一次インダクタンスや鉄損の影響がでてきますので， ある程度食い違うのは致し方ありません．

実機では，8 Ω にて 1W, 0.01W, 0.1mW となるよう入力を調整し， 負荷を 4 Ω に切り替えて出力電圧の変化を測定しました． 出力インピーダンス Zo の求め方は，

Zo = $\displaystyle {\frac{{e_2 - e_1}}{{e_1/R_{L1} - e_2/R_{L2}}}}$ (3.75)
です． ここで，e1 は RL1 を負荷としたときの出力電圧， e2 は RL2 を負荷としたときの出力電圧です．

結果は以下の通りです．

8 Ω 4 Ω Zo
出力電圧(V) 出力電圧(V) (Ω )
2.828 1.480 81.7
0.2828 0.1471 95.2
0.02832 0.01474 93.7

3.6.3 UL接続

シミュレーションによる各部の電圧・電流は， 図3.39のようになります．
図 3.39: UL接続の回路(シミュレーション)
Image UL_6L6_U-708_UL_sch

モデルによるロードラインと伝達特性は， 図3.40のようになります．

図 3.40: UL接続プレートロードライン・伝達特性(U-708 シミュレーション)
\includegraphics[width=\linewidth]{figs/6L6_U-708_UL_lltsim.ps}
青い破線は，静止時のロードラインで， 入力に 15.65Vp の信号を加え続けると， 2次歪みにより下降した平均プレート電圧が元にもどるため， 動作点はO'に移動し，ロードラインは実線のようになります． このロードラインは，プレート電流のみのため，湾曲しています． スクリーングリッド電流にSGタップ比率を掛けたものを加えたのが点線のロードラインで， 直線になります．

丸で示した点は，実機で観測された，オシロから読み取ったプレート電流です． 特性曲線が，特にグリッド電圧が深いところでずれているようですが， おおむね合っているといえるでしょう． 下側の線はスクリーングリッド電流を表しています．

実機で観測されたロードラインと伝達特性を， 図3.41，3.42に示します． 各部の波形を， 図3.43，3.44に示します．

図 3.41: UL接続プレートロードライン・伝達特性(U-708)
Image 6L6_U-708_UL_llt
図 3.42: UL接続SGロードライン・伝達特性(U-708)
Image 6L6_U-708_UL_lltIg2
図 3.43: UL接続のプレート電流の波形(U-708)
Image 6L6_U-708_UL_Ip
図 3.44: UL接続のスクリーングリッド電流の波形(U-708)
Image 6L6_U-708_UL_Ig2

グリッド電圧が -15 V あたりと -4 V のあたりで スクリーングリッド電流の増え方が急になります． モデルでは，この増え方が多少ゆるやかになっているようです．

今回の場合， rp = 57.882 kΩ ， gm(UL) = 3.878 mS ， μg1-g2 = 7.70 ですから， UL接続の内部抵抗 rp' は，

rp' = 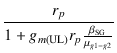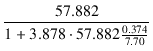$\displaystyle {\frac{{r_p}}{{1 + g_{m\rm (UL)} r_p \frac{\beta_{\rm SG}}{\micro_{g1{\rm -}g2}}}}}$ = $\displaystyle {\frac{{57.882}}{{1 + 3.878 \cdot 57.882 \frac{0.374}{7.70}}}}$ = 4.86 [kΩ] (3.76)
二次側から見た出力インピーダンス Zo は，

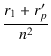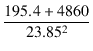Zo = r2 + $\displaystyle {\frac{{r_1 + r_p'}}{{n^2}}}$ = 0.43 + $\displaystyle {\frac{{195.4 + 4860}}{{23.85^2}}}$ = 9.32 [Ω] (3.77)
となります． ここで，r1 は一次巻線抵抗，r2 は二次巻線抵抗，n は巻数比です． シミュレーションでは 9.18 Ω となりました．

実機のON-OFF法による出力インピーダンスは以下の通りです．

8 Ω 4 Ω Zo
出力電圧(V) 出力電圧(V) (Ω )
2.828 1.851 8.94
0.2828 0.1855 8.83
0.0283 0.01857 8.81

OPT-10Sの場合，

rp' = 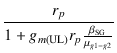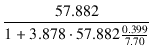$\displaystyle {\frac{{r_p}}{{1 + g_{m\rm (UL)} r_p \frac{\beta_{\rm SG}}{\micro_{g1{\rm -}g2}}}}}$ = $\displaystyle {\frac{{57.882}}{{1 + 3.878 \cdot 57.882 \frac{0.399}{7.70}}}}$ = 4.58 [kΩ] (3.78)
二次側から見た出力インピーダンス Zo は，

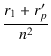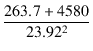Zo = r2 + $\displaystyle {\frac{{r_1 + r_p'}}{{n^2}}}$ = 0.72 + $\displaystyle {\frac{{263.7 + 4580}}{{23.92^2}}}$ = 9.19 [Ω] (3.79)
となります． 巻線抵抗が大きいため， SGタップ比率が高くても出力インピーダンスはそれほど下がりません． シミュレーションでは 9.08 Ω となりました．

実機のON-OFF法による出力インピーダンスは以下の通りです．

8 Ω 4 Ω Zo
出力電圧(V) 出力電圧(V) (Ω )
2.825 1.847 9.00
0.2826 0.1850 8.93
0.02823 0.01848 8.93

3.6.4 三極管接続

シミュレーションによる各部の電圧・電流は， 図3.45のようになります．

図 3.45: 三極管接続の回路(シミュレーション)
Image UL_6L6_U-708_tri_sch

モデルによるロードラインと伝達特性は， 図3.46のようになります．

図 3.46: 三極管接続プレートロードライン・伝達特性(U-708 シミュレーション)
\includegraphics[width=\linewidth]{figs/6L6_U-708_tri_lltsim.ps}
青い破線は，静止時のロードラインで， 入力に 20.01Vp の信号を加え続けると， 2次歪みにより下降した平均プレート電圧が元にもどるため， 動作点はO'に移動し，ロードラインは実線のようになります． このロードラインは，プレート電流のみのため，湾曲しています． スクリーングリッド電流を加えたのが点線のロードラインで， 直線になります．

丸で示した点は，実機で観測された，オシロから読み取ったプレート電流です． 特性曲線が，特にグリッド電圧が深いところでずれているようですが， おおむね合っているといえるでしょう． 下側の線はスクリーングリッド電流を表しています．

実機で観測されたロードラインと伝達特性を， 図3.47，3.48に示します． 各部の波形を， 図3.49，3.50に示します．

図 3.47: 三極管接続プレートロードライン・伝達特性(U-708)
Image 6L6_U-708_tri_llt
図 3.48: 三極管接続SGロードライン・伝達特性(U-708)
Image 6L6_U-708_tri_lltIg2
図 3.49: 三極管接続のプレート電流の波形(U-708)
Image 6L6_U-708_tri_Ip
図 3.50: 三極管接続のスクリーングリッド電流の波形(U-708)
Image 6L6_U-708_tri_Ig2

グリッド電圧が -15 V あたりと -4 V のあたりで スクリーングリッド電流の増え方が急になります． モデルでは，この増え方が多少ゆるやかになっているようです．

今回の場合， rp = 61.395 kΩ ， gm(UL) = 3.92 mS ， μg1-g2 = 7.65 ですから， 三極管続の内部抵抗 rp' は，

rp' = 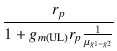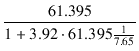$\displaystyle {\frac{{r_p}}{{1 + g_{m\rm (UL)} r_p \frac{1}{\micro_{g1{\rm -}g2}}}}}$ = $\displaystyle {\frac{{61.395}}{{1 + 3.92 \cdot 61.395 \frac{1}{7.65}}}}$ = 1.89 [kΩ] (3.80)
二次側から見た出力インピーダンス Zo は，

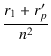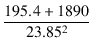Zo = r2 + $\displaystyle {\frac{{r_1 + r_p'}}{{n^2}}}$ = 0.43 + $\displaystyle {\frac{{195.4 + 1890}}{{23.85^2}}}$ = 4.10 [Ω] (3.81)
となります． シミュレーションでは， 4.07 Ω となりました．

実機のON-OFF法による出力インピーダンスは以下の通りです．

8 Ω 4 Ω Zo
出力電圧(V) 出力電圧(V) (Ω )
2.830 2.129 3.93
0.2828 0.2126 3.94
0.02826 0.02125 3.94

3.6.5 カソード帰還

シミュレーションによる各部の電圧・電流は， 図3.51のようになります．

図 3.51: カソード帰還の回路(シミュレーション)
Image UL_6L6_U-708_KF_sch

モデルによるロードラインと伝達特性は， 図3.52のようになります．

図 3.52: カソード帰還プレートロードライン・伝達特性(U-708 シミュレーション)
\includegraphics[width=\linewidth]{figs/6L6_U-708_KF_lltsim.ps}
青い破線は，静止時のロードラインで， 入力に 20Vp の信号を加え続けると， 2次歪みにより下降した平均プレート電圧が元にもどるため， 動作点はO'に移動し，ロードラインは実線のようになります． このロードラインは，プレート電流のみのため，湾曲しています． スクリーングリッド電流を加えたのが点線のロードラインで， 直線になります．

丸で示した点は，実機で観測された，オシロから読み取ったプレート電流です． 特性曲線が，特にグリッド電圧が深いところでずれているようですが， おおむね合っているといえるでしょう． 下側の線はスクリーングリッド電流を表しています．

実機で観測されたロードラインと伝達特性を， 図3.53，3.54に示します． 各部の波形を， 図3.55，3.56， 図3.57に示します．

図 3.53: カソード帰還プレートロードライン・伝達特性(U-708)
Image 6L6_U-708_KF_llt
図 3.54: カソード帰還SGロードライン・伝達特性(U-708)
Image 6L6_U-708_KF_lltIg2
図 3.55: カソード帰還のプレート電流の波形(U-708)
Image 6L6_U-708_KF_Ip
図 3.56: カソード帰還のスクリーングリッド電流の波形(U-708)
Image 6L6_U-708_KF_Ig2
図 3.57: カソード帰還のカソード電圧の波形(U-708)
Image 6L6_U-708_KF_Ek

グリッド電圧が -15 V あたりで スクリーングリッド電流の増え方が急になります． モデルでは，この増え方が多少ゆるやかになっているようです．

カソード帰還の場合は，一次および3次の巻線抵抗は 真空管の内部抵抗に直列に入っており， 負帰還の作用によって減少します． 今回の場合， rp = 57.166 kΩ ， gm(UL) = 3.80 mS ， μg1-g2 = 7.70 ですから， カソード帰還の内部抵抗 rp' は，

rp' = 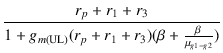$\displaystyle {\frac{{r_p+r_1+r_3}}{{1 + g_{m\rm (UL)} (r_p+r_1+r_3) (\beta + \frac{\beta}{\micro_{g1{\rm -}g2}})}}}$  
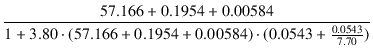  = $\displaystyle {\frac{{57.166+0.1954+0.00584}}{{1 + 3.80 \cdot (57.166+0.1954+0.00584)\cdot (0.0543 + \frac{0.0543}{7.70})}}}$ = 3.99 [kΩ] (3.82)

したがって，巻線抵抗はほぼ無視して構わないようです． 二次側から見た出力インピーダンス Zo は，

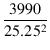Zo = r2 + $\displaystyle {\frac{{r_p'}}{{n^2}}}$ = 0.43 + $\displaystyle {\frac{{3990}}{{25.25^2}}}$ = 6.69 [Ω] (3.83)
となります． ここで，r1 は一次巻線抵抗，r2 は二次巻線抵抗， r3 はKNF巻線抵抗，n は巻数比です． シミュレーションによる出力抵抗は， 6.68 Ω でした．

実機のON-OFF法による出力インピーダンスは以下の通りです．

8 Ω 4 Ω Zo
出力電圧(V) 出力電圧(V) (Ω )
2.830 1.995 5.76
0.2828 0.2007 5.54
0.02829 0.02009 5.52
シミュレーションよりもだいぶ低い値になっています．

OPT-10Sの場合は，オートトランスとなるので， 出力インピーダンスを求める方法が異なります． 導出は省略しますが， 二次側から見た出力インピーダンス Zo は，

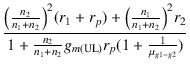
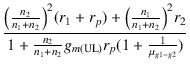Zo = $\displaystyle {\frac{{\big(\frac{n_2}{n_1+n_2}\big)^2(r_1+r_p) + \bigl(\frac{n_... ...+ \frac{n_2}{n_1+n_2} g_{m\rm (UL)} r_p (1 + \frac{1}{\micro_{g1{\rm -}g2}})}}}$ (3.84)
となります． ここで，r1 は一次巻線抵抗，r2 は二次巻線抵抗， n1 は一次巻数，n2 は二次巻数です． 数値を当てはめると，
Zo = $\displaystyle {\frac{{\big(\frac{n_2}{n_1+n_2}\big)^2(r_1+r_p) + \bigl(\frac{n_... ...+ \frac{n_2}{n_1+n_2} g_{m\rm (UL)} r_p (1 + \frac{1}{\micro_{g1{\rm -}g2}})}}}$  
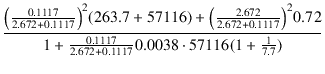  = $\displaystyle {\frac{{\big(\frac{0.1117}{2.672+0.1117}\big)^2(263.7+57116) + \b... ...72}}{{1 + \frac{0.1117}{2.672+0.1117} 0.0038 \cdot 57116 (1 + \frac{1}{7.7})}}}$ = 8.58 [Ω]  

となります． シミュレーションでは 8.35 Ω となりました．

実機のON-OFF法による出力インピーダンスは以下の通りです．

8 Ω 4 Ω Zo
出力電圧(V) 出力電圧(V) (Ω )
2.826 1.919 7.17
0.2832 0.1933 6.96
0.02829 0.01931 6.95

3.6.6 特性の比較

3.6.6.1 入出力特性

図 3.58: 入出力特性(U-708)
\includegraphics{figs/6L6_U-708_io.ps}
図 3.59: 入出力特性(OPT-10S)
\includegraphics{figs/6L6_OPT-10S_io.ps}
三極管接続は 1W 強でクリップしています． その他の回路では，3W 強の出力が得られました．

3.6.6.2 歪率特性

図 3.60: 歪率特性(U-708)
\includegraphics{figs/6L6_U-708_dist.ps}
図 3.61: 歪率特性(OPT-10S)
\includegraphics{figs/6L6_OPT-10S_dist.ps}
OPT-10SのKNFの歪率が少し悪くなっていますが， これは巻線のインピーダンスが低く，帰還量が少ないからです． 同程度の出力では，UL接続と三極管接続で歪率の差がほとんどありません． 三極管接続のほうが多少歪率が悪くなっています． KNFはコントロールグリッドに対する帰還なので， その分，歪率が低くなっています．

3.6.6.3 周波数特性

図 3.62: 周波数特性(U-708)
\includegraphics{figs/6L6_U-708_freq.ps}
図 3.63: 周波数特性(OPT-10S)
\includegraphics{figs/6L6_OPT-10S_freq.ps}
OPT-10SのUL接続では 45kHz 近辺にピークが見られます． このままでオーバーオールの負帰還をかけるのは少し危険でしょう． また，他の接続でも高域にアバレが見られます． さすがにTANGOのトランスは素直な特性です．

低域の特性は，三極管接続，KNF，UL接続，多極管接続の順で悪くなります． 高域の特性は，KNFが良く，その他はほとんど差がありません．

3.6.6.4 出力インピーダンス特性

注入法により測定した結果です．
図 3.64: 出力インピーダンス特性(U-708)
\includegraphics{figs/6L6_U-708_zo.ps}
図 3.65: 出力インピーダンス特性(OPT-10S)
\includegraphics{figs/6L6_OPT-10S_zo.ps}
ON-OFF法による結果と，ほとんど差がありません．
next up previous
Next: 4. プッシュプル出力段 Up: 3. 出力段の局部帰還(ウルトラリニアとカソード帰還) Previous: 3.5 数値例とシミュレーション
ayumi
2016-03-07