Next: 4.2 プッシュプルの動作階級 Up: 4. プッシュプル出力段 Previous: 4. プッシュプル出力段
プッシュプル接続の回路図を,図4.1に示します. プッシュプル接続では,一次巻線の中点にタップの付いた出力トランスを使い, 中点からプレート電圧を供給し, 一次巻線の両端に2本の真空管のプレートを接続します. 2本の真空管のグリッドには, 同じ振幅で,位相が逆の信号 eg を加えます.
直流プレート電流は,BからP1,BからP2へと反対方向に同じ大きさで流れるので, 出力トランスの鉄心は直流磁化されず, したがって鉄心にギャップを作る必要がなく, 小型の鉄心であっても一次巻線のインダクタンスを大きくできるため, シングル用の出力トランスと比べ, 小型で高性能のものが得られます. その代わり,V1とV2のプレート電流にわずかな(数mA)の差があっても, 直流磁化が起こってしまい,一次巻線のインダクタンスが急減するため, 直流バランスを取る必要があります.
次のように記号を定義します.
| Ebb = Eb0 | = | プレート電源電圧 | |
| Ecc = Ec0 | = | グリッドバイアス | |
| eg | = | グリッド入力信号の瞬時値 | |
| ec | = | グリッド電圧の瞬時値 | |
| ib | = | プレート電流の瞬時値 | |
| Ib0 | = | 無信号時のプレート電流 | |
| io | = | 出力トランスに流れる信号電流の瞬時値 | |
| eo | = | 出力トランスの一次巻線の半分に生じる電圧の瞬時値 | |
| RL | = | 負荷抵抗 | |
| iL | = | 負荷に流れる電流の瞬時値 | |
| eL | = | 負荷の両端に生じる電圧の瞬時値 | |
| N1 | = | 出力トランスの一次巻線の半分の巻数 | |
| N2 | = | 出力トランスの二次巻線の巻数 | |
| RL |
= | 一次巻線の半分からみた負荷抵抗 = |
|
| Rpp | = | 一次巻線からみたプレート-プレート間負荷抵抗 = 4 |
信号を加えていない静止時の動作を調べると,
2本の真空管のグリッド電圧,プレート電圧,プレート電流が
同一であることがわかります.
| ec1 | = | ec2 = Ecc = Ec0 | (4.1) |
| eb1 | = | eb2 = Ebb = Eb0 | (4.2) |
| ib1 | = | ib2 = Ib0 | (4.3) |
信号が加えられると,2本の真空管のグリッド電圧は逆方向に変化し,
2本の真空管のプレートが出力トランスの一次巻線に接続されているため,
プレート電圧の変化も同じ大きさで逆方向になります.
| = | - |
(4.4) | |
| = | - |
(4.5) |
![]() ec1
が正のとき,
ec1
が正のとき,
| ec1 | = | Ec0 + |
(4.6) |
| ec2 | = | Ec0 + |
(4.7) |
トランスの一次巻線の起磁力(アンペア回数)は, V1については N1io1 , V2については N1io2 であり, io1 と io2 の方向が同じであることから, N1 回巻の巻線に io1 + io2 = io の電流が流れた場合の起磁力と等しくなります. この,総起磁力と二次巻線のアンペア回数が等しくなるので,
| N1(io1 + io2) = N2iL | (4.12) |
| eL = iLRL | (4.13) |
であるから,これを式(4.16)に代入して, となります.
この関係は,横軸にV1のプレート電圧(eb1
)をとり,
縦軸にV1とV2のプレート電流の差をとれば,
式(4.10)より,
![]() eb1 = - eo
であるから,
eb1 = - eo
であるから,
| eb1 | = | Eb0 - eo | |
| eo | = | Eb0 - eb1 |
また,式(4.16)より,
| = | |||
| = | (4.20) |
信号が加えられた時のプレート電圧とプレート電流(の差)の組み合わせは, 式(4.19)の直線(合成ロードライン)上にあります. この直線上のどの点になるのかを求めるには, ある信号が加えられた時の,プレート電圧と,プレート電流の差の関係を知る必要があります.
信号 eg
が加えられると,それぞれのグリッド電圧は
| ec1 | = | Ec0 + eg | (4.21) |
| ec2 | = | Ec0 - eg | (4.22) |
プレート電圧の関係は,式(4.10), (4.11)より,
![]() eb1
を消去して,
eb1
を消去して,
これらのことから,V1のグリッド電圧,プレート電圧が決まれば, V2のグリッド電圧,プレート電圧が決まりますので, V1側のグリッド電圧,プレート電圧だけに注目して ib1 - ib2 を求めます. これをプレート特性図を使って行うには, 2枚のプレート特性図を用意し,V2に相当する片側を180度回転し, Eb0 が一致するように横軸を貼りあわせます(図4.2). こうすると,式(4.26)の条件が満たされます. このとき,上側の特性図のプレート電流は ib1 となり, 下側の特性図のプレート電流は, 方向が逆向きになっているので - ib2 を表しています.
グリッド電圧に関する制約(式(4.24))を満たすV1とV2のグリッド電圧を選び出し, さまざまなV1のプレート電圧について,ib1 と - ib2 を加算していきます. これは,eb1 を通る垂線を引き, それと上側の ec1 の特性曲線と交わる点のy 座標(ib1 )を求め, eb1 を通る垂線と下側の ec2 の特性曲線が交わる点のy 座標(-ib2 )を 求め,足した値を垂線上にプロットすることで達成されます.
ここでは例として, ec1 = - 40 V, eb1 = 250 Vの場合を検討します. 式(4.24)より,
となります. これらのグリッド電圧に対応する特性曲線は青い線で表わされています. この特性曲線上の eb1 = 250 Vのプレート電流を求めると, V1のプレート電流は点Bの78.6mA, V2のプレート電流は点Cの18.3mAとなるので, 合成プレート電流は, 78.6 - 18.3 = 60.4 mAとなり,点Dが対応します. 同じグリッド電圧でプレート電圧が225Vの場合, V1のプレート電流は点B' の47.1mA, V2のプレート電流は点C' の38.8mAとなるので, 合成プレート電流は, 47.1 - 38.8 = 8.3 mAとなり,点D' が対応します.
この作業を eb1 の値を変えながら繰り返していくと, ib1 - ib2 の軌跡はほぼ直線になります. さきほどの eb1 = - 40 Vの場合, この軌跡は黄色の線のようになります.
いくつかの ec1 の値について ib1 - ib2 の軌跡を描いたものが, プッシュプルの合成プレート特性図になります. 合成プレート特性は,特定の Eb0 と Ec0 についてのものです. これらの条件が変わったら,作成しなおす必要があります.
たとえば,先ほどの例で Rpp = 5 kΩ のとき, 合成ロードラインは太い青色の線になり, ec1 = - 40 Vとなったとき, 合成プレート特性曲線と合成ロードラインの交点はD' となり, プレート電圧は242.9V,合成プレート電流は45.7mAとなります. このとき,V1のプレート電流は, 同じプレート電圧上の ec1 = - 40 Vの特性曲線上の点B' から読み取れ,69.1mAです. 同様にして,V2のプレート電流は,点C' の23.4mAとなります. このようにして個々の真空管のプレート電圧とプレート電流の軌跡を求めると, 水色の線のようになり,かなり弓なりになっています. この個々の真空管のロードラインは,個々の真空管の動作点Aを通ります.
また点A近辺では,2本の真空管はほぼ同じ条件で動作しており,
RL![]() = Rpp/4
を2本の真空管で並列に駆動していることになり,
一本あたりの負荷は Rpp/2
となります.
この負荷に相当するロードラインを青色の細い線で描いてあります.
このロードラインと水色の個々の真空管のロードラインは,
動作点Aでは接しています.
= Rpp/4
を2本の真空管で並列に駆動していることになり,
一本あたりの負荷は Rpp/2
となります.
この負荷に相当するロードラインを青色の細い線で描いてあります.
このロードラインと水色の個々の真空管のロードラインは,
動作点Aでは接しています.
入力電圧(eg )を横軸にとり,縦軸に各球のプレート電流と合成プレート電流をとれば,伝達特性が得られます(図4.4). 水色の線が各球の伝達特性で,青い線が合成伝達特性です. ご覧のように,各球のプレート電流は,入力電圧に比例しているわけではありません(2次 歪みが発生している)が,合成プレート電流は,ほぼ入力電圧に比例しています.
|
(Eb0 - Ep min) x 2 x |
(4.27) |
Po = 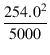 = 12.9 [W] = 12.9 [W]
|
(4.28) |
また,合成出力電流の実効値は
Ip max/![]() なので,
次のようにしても出力を求められます.
なので,
次のようにしても出力を求められます.
Po = 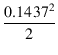 x 1250 = 12.9 [W] x 1250 = 12.9 [W]
|
(4.29) |
プッシュプル出力段をそのまま等価回路にすると, 図4.5 (a)のようになりますが,
電圧源と内部抵抗をまとめると,同図(b)となります.
したがって,片グリッド-グラウンドの入力 eg
から,
プレート-プレート間のゲインは,
| eo | = | - 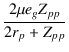 |
(4.30) |
| A | = | - 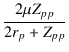 |
(4.31) |
| Zo = 2rp | (4.32) |
|
|
(4.33) |
第4.1.1節より, プッシュプルの2本の真空管の信号電流は, 加算されて(並列接続で)一次巻線の半分を流れると解釈することもできます. こう考えると,等価回路は図4.6 (a)となります.
並列接続されている電圧源と内部抵抗をまとめると,同図(b)となります.
したがって,片グリッド-グラウンドの入力 eg
から,
プレート-グラウンド間のゲインは,
| eo | = | - 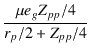 - - 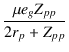 |
(4.34) |
| A | = | - 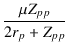 |
(4.35) |
| Zo = rp/2 | (4.36) |
|
|
(4.37) |
ayumi