4.3 最適負荷抵抗

合成プレート特性が直線であると仮定します． V1のグリッド電圧が0Vの合成特性曲線をMPとします．

**図 4.14:** プッシュプルの最適負荷抵抗
$\begin{figure}\input{figs/pp_opt_rl} \end{figure}$

プレート電圧が E_b0 のときのプレート電流を I_E₀ とすると，特性曲線は， (E_b0, I_E₀) (点M)を通る傾きが 1/r_p の直線なので，

i_b = $\displaystyle {\frac{{e_b - E_{b0}}}{{r_p}}}$ + I_E₀

(4.43)

この特性曲線と合成ロードラインの交点をAとします．このときのプレート電圧を e_pmin ，プレート電流を i_pmax とすれば，出力 P_o は，

P_o = 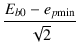$\displaystyle {\frac{{E_{b0} - e_{p\rm min}}}{{\sqrt{2}}}}$ ^. $\displaystyle {\frac{{i_{p\rm max}}}{{\sqrt{2}}}}$ = $\displaystyle {\frac{{1}}{{2}}}$ (E_b0 - e_pmin)i_pmax

(4.44)

P_o = $\displaystyle {\frac{{1}}{{2}}}$ e_oi_pmax

(4.45)

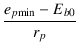i_pmax = $\displaystyle {\frac{{e_{p\rm min} - E_{b0}}}{{r_p}}}$ + I_E₀ = - $\displaystyle {\frac{{e_o}}{{r_p}}}$ + I_E₀

(4.46)

P_o	=	$\displaystyle {\frac{{1}}{{2}}}$ $\displaystyle \biggl($ - $\displaystyle {\frac{{{e_o}^2}}{{r_p}}}$ + e_oI_E₀ $\displaystyle \biggr)$
	=	- $\displaystyle {\frac{{1}}{{2 r_p}}}$ (e_o² - I_E₀r_pe_o)
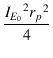	=	- $\displaystyle {\frac{{1}}{{2 r_p}}}$ $\displaystyle \biggl\{$ $\displaystyle \biggl($ e_o - $\displaystyle {\frac{{I_{E_0} r_p}}{{2}}}$ $\displaystyle \biggr)^{2}_{}$ - $\displaystyle {\frac{{{I_{E_0}}^2 {r_p}^2}}{{4}}}$ $\displaystyle \biggr\}$

P_omax = $\displaystyle {\frac{{{I_{E_0}}^2 r_p}}{{8}}}$

(4.47)

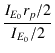R_L = $\displaystyle {\frac{{e_o}}{{i_{p\rm max}}}}$ = $\displaystyle {\frac{{I_{E_0} r_p / 2}}{{I_{E_0} / 2}}}$ = r_p

(4.48)

4.3.1.2 シミュレーション

プッシュプルの場合，一方の真空管がカットオフしても大きな歪が発生しないので，常にグリッド電圧が0Vになるまで入力を加えることができます．

しかし，負荷抵抗を低くしていくと，プレート電流の尖頭値が大きくなり，プレート損失も大きくなります．したがって，プレート損失の定格により，負荷抵抗の最低値が制限されます．

図4.15に， 2A3を E_p0 = 300 V， E_g0 = - 61 Vで動作させ，合成負荷抵抗を変化させた場合の，出力(Po)，プレート損失(Pd)，歪率を示します．

**図 4.15:** 三極管ppで負荷インピーダンスを変化させた場合の最大出力と歪率
$\includegraphics{figs/tripp_PoK_RL.ps}$

合成プレート抵抗は508Ω 程度で，それと同じ負荷抵抗のときに出力が最大値となりますが，プレート損失の制限により，そのような状況で動作させることはできません．

図4.16に，負荷抵抗を3kΩ とした場合の入出力特性を示します．

出力が増えるにつれ，プレート電流(Ip：水色)が増え，プレート損失(Pd：青)がわずかに増えています．歪率(THD：緑)は，出力に比例しています．

**図 4.16:** 三極管ppの入出力特性
$\includegraphics{figs/tripp_PoK_IO.ps}$

4.3.2 多極管の場合

多極管の場合は，プレート抵抗と負荷抵抗がかけ離れた状態で動作させるため，三極管のように最適負荷をプレート抵抗から求めることはできません．出力を大きくするには，図4.14の点Aをできるだけ左上に位置させる必要があるため，多極管の場合に最大出力を得るには，特性曲線のニーポイント(特性曲線が折れ曲がる点)を通るようにロードラインを引きます．これより負荷抵抗が高いと，グリッド電圧を0Vまで励振する前にクリップしてしまいます．負荷抵抗が低いと，プレート電流の尖頭値が大きくならない一方で，出力電圧の尖頭値が小さくなるため，出力が減ってしまいます．

図4.17に， 6L6-GCを E_p0 = 360 V， E_g20 = 270 V， E_g0 = - 22.5 Vで動作させ，合成負荷抵抗を変化させた場合の，出力(Po)，プレート損失(Pd)，歪率を示します．

図: 6L6 AB₁ 級ppで負荷インピーダンスを変化させた場合の最大出力と歪率
$\includegraphics{figs/beampp_PoK_RL.ps}$

ニーポイントを通るロードラインの場合に，最も歪が小さくなります．ロードラインがニーポイントを外れると，急速に最大出力が下がります．負荷抵抗を最適値より高くすると，フルスイングしたときに激しくクリップし，歪が急増します．そのとき，スクリーングリッド損失(Pg2)が急速に増大します．最大出力時のスクリーングリッド損失が定格を超えている場合には，スクリーン電圧を下げて設計しなおします．

負荷抵抗を6.6kΩ とした場合の特性曲線とロードラインを図4.18に，

出力が増えるにつれ，プレート電流(Ip：マゼンタ)が増えますが，プレート損失(Pd：青)は減っています．スクリーングリッド電流(Ig2：黄)の増え方は，プレート電流よりも大きくなっています．プレート電圧が100Vを下回ってくると，急速にスクリーングリッド電流が多くなるからです．歪率(THD：緑)は，最大出力の少し手前から下がっています．ニーポイント近辺で特性曲線が曲がっているため，縦方向に伸びていた波形の頭がわずかに潰れてくるため， 3次歪が減り，5次歪が増えているためです．

4.3 最適負荷抵抗

4.3.1 三極管の場合

4.3.1.1 理想三極管の場合

4.3.1.2 シミュレーション

4.3.2 多極管の場合