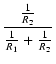


Next: A.3 テブナンの定理,ノートンの定理
Up: A. 基礎知識
Previous: A.1 抵抗,コンデンサ,インダクタ
図A.4のように,2つの抵抗 R1, R2 を直列に接続し,
その両端に V という電圧が掛かっている場合を考えます.
2本の抵抗に流れる電流は等しいので,それを I とします.
それぞれの抵抗の両端の電圧を V1, V2 とすれば,
それぞれの抵抗についてオームの法則が成り立つので,
したがって,
|
V = V1 + V2 = IR1 + IR2 = I(R1 + R2)
|
(A.19) |
となります.
これより,2本の抵抗の合成抵抗 R は,
R = 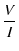 = R1 + R2 = R1 + R2
|
(A.20) |
となります.
つまり,2本の抵抗を直列に接続すると,
抵抗値が2本の抵抗値の和と等しい抵抗に見えることになります.
図 A.4:
抵抗の直列接続
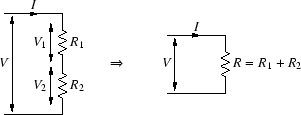 |
また,下側の抵抗の両端に発生する電圧 V2 と,
全体の電圧 V の関係は,
V2 = IR2 = 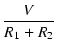 R2 = V R2 = V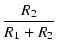
|
(A.21) |
となり,抵抗値の比率で電圧が分圧されていることがわかります.
ここでは抵抗を用いましたが,
R の替わりに ZL, ZC を用いれば,
インダクタ,コンデンサ等に対しても同様な式が成り立ちます.
図A.5のように,2つの抵抗 R1, R2 を並列に接続し,
その両端に V という電圧が掛かっている場合を考えます.
それぞれの抵抗に流れる電流を I1, I2 とすれば,
それぞれの抵抗についてオームの法則が成り立つので,
| I1 |
= |
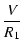 |
|
| I2 |
= |
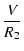 |
|
したがって,回路全体に流れる電流 I は,
I = I1 + I2 = 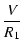 + + 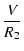 = V = V 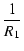 + + 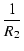 
|
(A.22) |
となります.
これより,2本の抵抗の合成抵抗 R は,
| R |
= |
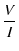 = = 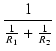 = = 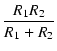 |
(A.23) |
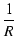 |
= |
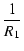 + + 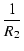 |
(A.24) |
となります.
つまり,2本の抵抗を並列に接続すると,
アドミッタンス(抵抗値の逆数)が2本の抵抗のアドミッタンスの和と等しい抵抗に見えることになります.
図 A.5:
抵抗の並列接続
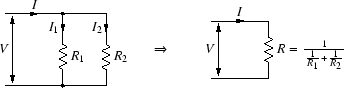 |
また,右側の抵抗を流れる電流 I2 と,
全体の電流 I の関係は,
となり,アドミッタンスの比率で電流が分流されていることがわかります.



Next: A.3 テブナンの定理,ノートンの定理
Up: A. 基礎知識
Previous: A.1 抵抗,コンデンサ,インダクタ
平成18年3月22日
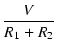 R2 = V
R2 = V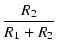
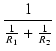 =
= 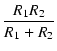
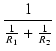 = I
= I