Next: この文書について... Up: 定インピーダンスアッテネータの製作 Previous: 3 測定
定インピーダンスアッテネータとフィルタでは, 信号源抵抗 RS と 負荷抵抗 RL が共に R であると仮定してきましたが, この制約を外します. また計算を簡単にするため,橋絡T型ではなくT型で検討します. 回路図は図9となります.
これより,
| Vo | = | 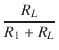 V2 V2 |
(1) |
| V2 | = | 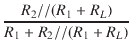 V1 V1 |
|
| = | 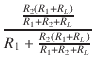 V1 = V1 = 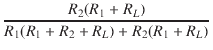 V1 V1 |
(2) | |
| V1 | = | 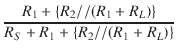 VS VS |
|
| = | 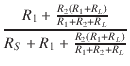 VS = VS = 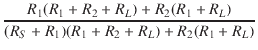 VS VS |
(3) | |
| V2 | = | 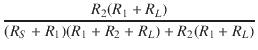 VS VS |
(4) |
| Vo | = | 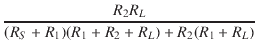 VS VS |
(5) |
| R1 | = | (8) | |
| R2 | = | 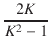 R R |
(9) |
| K1 | = | 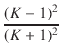 R2 . R2 . 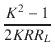 +2 +2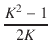 + 1 + 1 |
|
| = | 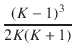 . . 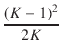 + 1 + 1 |
||
| = | 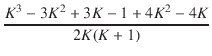 . . 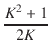 |
||
| = | 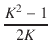 . . 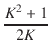 |
(10) | |
| KS | = | K1 + 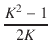 +1 +1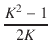 . . |
|
| = | K1 + 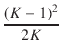 +1 +1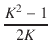 . . |
||
| = | K1 + 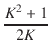 . . 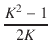 . . |
(11) |
| K1 | = | 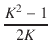 + + 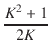 = = |
(12) |
| KS | = | K1 + 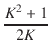 + + 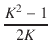 = K + = K + |
(13) |
| K1 | = | K | (14) |
| KS | = | K1 + 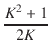 . . 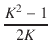 . . |
|
| = | 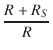 K K |
(15) |
| K1 | = | 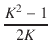 . . 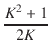 |
(16) |
| KS | = | K1 + 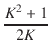 . . 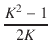 |
|
| = | 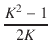 . . 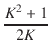 + + 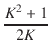 . . 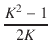 |
||
| = | 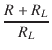 K K |
(17) |
RL = R として減衰量を0dBから20dBまで2dBステップで変化させ,RS を変化させた場合の K1 および K の変化を図10に示します.
赤い線,すなわちアッテネータの入力から出力までの減衰量は, RS が変化しても一定の値(設計値)を取ります. 電圧源からの減衰量である青い線も一定間隔であり, アッテネータとして正しく動作することがわかります. 信号源インピーダンスが設計値であれば,すなわち RS/R = 1 であれば, 信号源からの減衰量は設計値より6dB大きくなります.RS = R として減衰量を0dBから20dBまで2dBステップで変化させ,RL を変化させた場合の K1 および K の変化を図11に示します.
赤い線,すなわちアッテネータの入力から出力までの減衰量は, 間隔が一定ではなく,減衰量が等間隔で変化しなくなってしまいます. RL/R が大きいと,減衰量が小さいときに設計値よりも減衰量が小さくなってしまい, 逆に RL/R が小さいと,減衰量が小さいときに設計値よりも減衰量が大きくなってしまいます. 減衰量が大きい場合は相対的に正しく動作するようです. 一方,電圧源からの減衰量である青い線は一定間隔であり, アッテネータとして正しく動作することがわかります.
ロー出しハイ受けの場合の例を,図12に示します.
ここでは,
R = 600 ![]() ,
RS = 100
,
RS = 100 ![]() としています.
RL = 10 k
としています.
RL = 10 k![]() とすると,
RL/R = 16.67 となります.
青い線の間隔が下の方で詰まっているので,
減衰量が小さいとほとんど減衰しなくなってしまいます.
赤い線は信号源抵抗と関係ないので,図11と同じです.
とすると,
RL/R = 16.67 となります.
青い線の間隔が下の方で詰まっているので,
減衰量が小さいとほとんど減衰しなくなってしまいます.
赤い線は信号源抵抗と関係ないので,図11と同じです.
以上のように,信号源抵抗 RS または負荷抵抗 RL のいずれかが設計値であれば, アッテネータとして正しく動作します.
一般に,最近のオペアンプ出力のオーディオ機器では出力インピーダンスが100![]() 程度ですが,
600
程度ですが,
600![]() 負荷に耐えられるかは微妙です.
仮に出力インピーダンスが100
負荷に耐えられるかは微妙です.
仮に出力インピーダンスが100![]() であるとして,600
であるとして,600![]() を負荷としたアッテネータを駆動すると,
高インピーダンス負荷の場合と比べて出力が6/7となります.
600
を負荷としたアッテネータを駆動すると,
高インピーダンス負荷の場合と比べて出力が6/7となります.
600![]() の負荷を駆動できる(NE5532など)であれば,この方法で使えます.
一般に,図13のように620
の負荷を駆動できる(NE5532など)であれば,この方法で使えます.
一般に,図13のように620![]() 程度を次段の機器の入力端子と並列に接続します.
程度を次段の機器の入力端子と並列に接続します.
信号源インピーダンスを600![]() に変更できる場合は,
アッテネータに接続する機器のインピーダンスは高くてもよく,
その場合,オペアンプの負荷は最悪で1.2k
に変更できる場合は,
アッテネータに接続する機器のインピーダンスは高くてもよく,
その場合,オペアンプの負荷は最悪で1.2k![]() になりますので,
先ほどの場合よりも負荷が軽く,またレベルの減衰も少なくなります.
図14のように510
になりますので,
先ほどの場合よりも負荷が軽く,またレベルの減衰も少なくなります.
図14のように510![]() 程度を前段の機器の出力端子と直列に接続し,
信号源の出力インピーダンスを適切に調整できるのであれば,
こちらの方法のほうが良いのではないかと思います.
程度を前段の機器の出力端子と直列に接続し,
信号源の出力インピーダンスを適切に調整できるのであれば,
こちらの方法のほうが良いのではないかと思います.