Next: 4 オルソンアンプの製作 Up: オルソンアンプの解析 Previous: 2 オルソンアンプの原回路
原論文には各部の電圧が記載されていません. シミュレーションの回路図を図2に示します. 電源電圧を 390V と仮定しています. 各部の電圧および電流は,回路図に記載されたとおりです. 原回路の出力トランスは,ユニバーサルタイプということで, シミュレーションではそれほど高級品ではないタムラF-483を選んでいます. このトランスの定格一次インピーダンスは 5 kΩ なので, 一次のインピーダンスが 4.5 kΩ になるよう, 負荷抵抗の値を 7.088473 Ω としています.
この段のバイアスは -7.672 V とかなり深くなっていますが, ピックアップからボリュームを経ずに入力されているため, この段で歪みが生じないようにするためと思われます. ゲインは12.1倍です.
次段がPK分割の位相反転になっているため, R11の見かけ上のインピーダンスが 2.1 MΩ 程度となり, ほとんど無視することができます. この段のバイアスは -3.231 V と非常に浅く, 6F6をドライブするのに足るだけの信号を増幅できるぎりぎりの設計となっています. この段のゲインは16.1倍です.
実際は,この回路のゲインを正確に求めることは困難です. R11が出力につながっているためで, R11を通った入力電流がカソード側の出力に加わるためです.
導出の詳細は省きますが,
プレート側とカソード側のそれぞれのゲインと,
ゲインを揃えるためのR13の値は,次のようになります.
| Ap | = | - 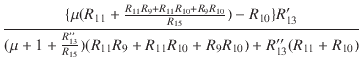 |
(1) |
| Ak | = | 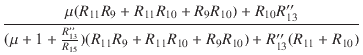 |
(2) |
| R13'* | = | 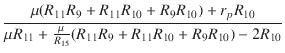 |
(3) |
| R13' | = | R13//R14 | |
| R13” | = | rp + R13' |
この式を使ってゲインを求めると,
| Ap | = | -0.8749 | |
| Ak | = | 0.8812 |
| R13'* | = | 36494 [Ω] | |
| R13* | = | 39306 [Ω] |
[3]の作例ではR9+R10とR13の値を揃えています. また,[4]の作例では,R9にバイパスコンデンサを抱かせ, R10とR13の値を等しくしています. これらの処置は,かえってバランスを崩します. 前者では約 0.13dB,後者では約 0.03dB の偏差が生じています. 後者では,R11の値が大きくなっているため,偏差が小さくなっています.
出力段の動作点は,
Ep0 = 347.1 V,
Eg0 = - 34.41 V,
Ip0 = 28.67 mA,
gm = 2.261 mS,
rp = 2.928 kΩ,
![]() = 6.620 です.
ロードラインを図9に示します.
= 6.620 です.
ロードラインを図9に示します.
片側のゲインおよびダンピングファクターは,
| A | = | -6.620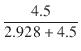 = 4.011 = 4.011 |
(4) |
| DF | = | (5) |
Po = 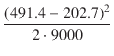 = 4.63 [W] = 4.63 [W]
|
(6) |
なお,この歪率は,無限大の一次インダクタンス, 浮遊容量0,巻線抵抗が0の,理想的な状態のものです. また,オルソンアンプは自己バイアスですので, 最大出力時にはプレート電流が増え,バイアスが深くなりますが, 上記の歪率は,最大出力の信号を連続的に出力している場合ではなく, 最大出力が出た瞬間のものに相当します. 実際には,使用する出力トランスによって歪率が異なります. 以下に,さまざまなトランスを使用した場合の歪率のシミュレーション結果を示します.
| トランス | 一次インダクタンス | バイアス | 二次側出力 | 歪率 |
| 理想 | 400H | 固定 | 9.041W | 1.148% |
| 理想 | 27.7H | 固定 | 9.038W | 1.155% |
| F-2021 | 123.7H | 固定 | 8.328W | 1.071% |
| F-483 | 27.7H | 固定 | 7.725W | 0.990% |
| F-483 | 27.7H | 自己(1-2ms) | 7.610W | 0.995% |
| F-483 | 27.7H | 自己(99-100ms) | 7.169W | 0.991% |
| F-483 | 27.7H | 自己(Ckなし) | 6.829W | 1.301% |
これらのロードラインを,図10に示します.
F-2021を使用した場合の負荷は容量性になり, それ以外の負荷は誘導性です. 同じインダクタンスの理想トランスとF-483でもロードラインの膨らみ方が違うのは, F-483の場合,浮遊容量が入っており,誘導性と容量性が打ち消し合っているからです.自己バイアスの場合,約 30ms 後に定常状態になりますが, その時のカソード電圧は約 36.26V に上昇し, 総プレート電流は 120.9mA となります. この時定数は,R16とC9によるものですが, 収束する時間は,時定数から計算されたものよりも短くなります.
| Zo1 | = | rp1//R4 = 10.52//22 = 7.12 [kΩ] | |
| Tl1-2 | = | C3(Zo1 + R6 + R7) = 10.4 [ms] | |
| fl1-2 | = | 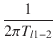 = 15.29 [Hz] = 15.29 [Hz] |
|
| Th1-2 | = | {Cgk2 + (1 + A2)Cgp2}{(Zo1 + R6)//R7} | |
| = | {3 + (1 + 16.1)4}{(7.12 + 47)//50} . 10-9 = 1.86 [μs] | ||
| fh1-2 | = | 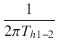 = 85.8 [kHz] = 85.8 [kHz] |
| Zo2 | = | rp2//R12 = 7.333//22 = 5.5 [kΩ] | |
| Tl2-3 | = | C6(Zo2 + R11') = 63.2 [ms] | |
| fl2-3 | = | 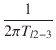 = 2.52 [Hz] = 2.52 [Hz] |
|
| Th2-3 | {(1 + A3)Cgp3}Zo2 | ||
| = | {(1 + 0.88)4}5.5 . 10-9 = 41.4 [ns] | ||
| fh2-3 | = | 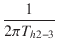 = 3.85 [MHz] = 3.85 [MHz] |
| Tl2 | = | ||
| = | 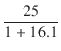 {(1 + 16.1)0.39//(7.333 + 22)} . 10-3 = 7.94 [ms] {(1 + 16.1)0.39//(7.333 + 22)} . 10-3 = 7.94 [ms] |
||
| fl2 | = |
| Zo3 | = | 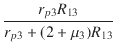 |
|
| = | 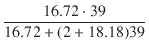 = 0.811 [kΩ] = 0.811 [kΩ] |
||
| Tl3-4 | = | C7(Zo3 + R14) = 25.5 [ms] | |
| fl3-4 | = | 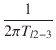 = 6.23 [Hz] = 6.23 [Hz] |
|
| Th3-4 | = | {Cgk4 + (1 + A4)Cgp4}Zo3 | |
| = | {10 + (1 + 4.011)8}0.811 . 10-9 = 40.6 [ns] | ||
| fh3-4 | = | 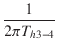 = 3.92 [MHz] = 3.92 [MHz] |
| Tlt | = | 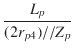 = 10.9 [ms] = 10.9 [ms] |
|
| flt | = |
各段の周波数特性と,総合周波数特性を,図11に示します.
全体の周波数特性(マゼンタ)は, 入力から2段目までの特性(赤)によってほぼ支配されているようです. 位相反転段から出力段の周波数特性は, 高域においてプレート側(青)とカソード側(水色)で違っています. これを改善するには,カソード側に 9pF 程度のコンデンサを付加します.
グラフからは出力が飽和したようには見えませんが, 7W 相当の入力を加えると,瞬間的にクリップするので, このあたりが実用的な最大出力になります. 歪率は 7W 時に2.5%程度なので,オルソン博士が設定した目標をクリアしています.
この時の出力段のグリッド入力の波形を,図16に示します. 上下の球が対称な動作をしておらず,気持ち悪いのですが出力の歪みは小さくなります.