Next: 2.4 グリッド接地 Up: 2. 電圧増幅回路 Previous: 2.2 電流帰還

2.3 プレート接地(カソードフォロワ)

プレート接地増幅回路の例を図2.7に示します．自己バイアスのバイパスコンデンサ C_k を省き， R_k + R_L を負荷抵抗とした回路もありますが，後にシミュレーションでわかるとおり，性能は大差ありません．この場合，出力は R_k と R_L の接続点からではなく，カソードから取り出します．

**図 2.7:** プレート接地増幅回路
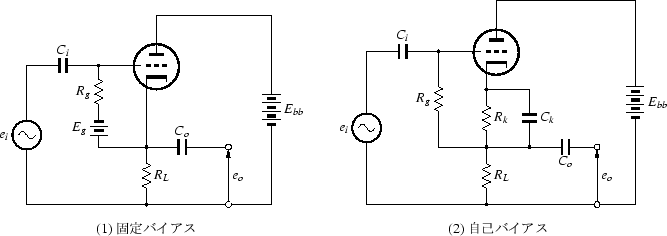
$\begin{figure}\input{figs/com_p} \end{figure}$

等価回路は図2.8になります．

**図 2.8:** プレート接地の等価回路
$\begin{figure}\input{figs/com_p_equiv} \end{figure}$

これより，次の関係が成り立ちます．

e_o	=	(i₁ + i₂)R_L	(2.14)
μe_g	=	e_o + i₂r_p	(2.15)
e_i	=	e_o + i₁R_g	(2.16)
e_i	=	e_g + e_o	(2.17)

これより増幅度 A を求めると，

e_g	=	e_i - e_o
μe_i - μe_o	=	e_o + i₂r_p
μe_i	=	(1 + μ)e_o + i₂r_p
μR_ge_i	=	(1 + μ)R_ge_o + i₂r_pR_g
r_pe_i	=	r_pe_o + i₁r_pR_g
(r_p + μR_g)e_i	=	{(1 + μ)R_g + r_p}e_o + (i₁ + i₂)r_pR_g
(r_p + μR_g)e_i	=	{(1 + μ)R_g + r_p}e_o + $\displaystyle {\frac{{e_o}}{{R_L}}}$ r_pR_g
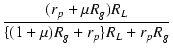e_o	=	$\displaystyle {\frac{{(r_p+\micro R_g)R_L}}{{\{(1+\micro)R_g+r_p\}R_L+r_p R_g}}}$ e_i
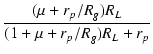	=	$\displaystyle {\frac{{(\micro+r_p/R_g)R_L}}{{(1+\micro+r_p/R_g)R_L+r_p}}}$ e_i
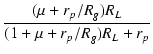A	=	$\displaystyle {\frac{{(\micro+r_p/R_g)R_L}}{{(1+\micro+r_p/R_g)R_L+r_p}}}$	(2.18)

となります． R_g $\gg$ r_p とすると，

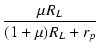
A $\displaystyle \approx$ $\displaystyle {\frac{{\micro R_L}}{{(1+\micro)R_L+r_p}}}$

(2.19)

となります．

入力インピーダンスは，入力信号の電圧 e_i と電流 i₁ から求められます．

i₁	=	$\displaystyle {\frac{{e_i - e_o}}{{R_g}}}$ = $\displaystyle {\frac{{e_i (1-A)}}{{R_g}}}$
Z_i	=	$\displaystyle {\frac{{e_i}}{{i_1}}}$ = $\displaystyle {\frac{{R_g}}{{1-A}}}$ = $\displaystyle {\frac{{r_p+(1+\micro+r_p/R_g)R_L}}{{r_p+R_L}}}$ R_g	(2.20)
	$\displaystyle \approx$	$\displaystyle {\frac{{r_p+(1+\micro)R_L}}{{r_p+R_L}}}$ R_g = $\displaystyle \biggl($ 1 + $\displaystyle {\frac{{\micro R_L}}{{r_p+R_L}}}$ $\displaystyle \biggr)$ R_g = $\displaystyle \biggl($ 1 + g_m $\displaystyle {\frac{{r_p R_L}}{{r_p + R_L}}}$ $\displaystyle \biggr)$ R_g	(2.21)

r_p $\ll$ R_L とすると，入力インピーダンスはグリッド抵抗のほぼ μ 倍 (より正確にはカソード接地の増幅度倍)となります．五極管の場合は， r_p $\gg$ R_L となり，入力インピーダンスは R_g のほぼ g_mR_L 倍となります．

出力インピーダンスを求めるには，入力を短絡し，出力端子に e_o を加えた等価回路を作成し，出力端子から回路に流れ込む電流 i_o を求め， Z_o = e_o/i_o により出力インピーダンスを求めます．出力インピーダンスを求めるための等価回路を図2.9に示します．

**図 2.9:** プレート接地の出力インピーダンスを求めるための等価回路
$\begin{figure}\input{figs/com_p_zo} \end{figure}$

e_i	=	e_g + e_o = 0
e_g	=	- e_o
i₁	=	$\displaystyle {\frac{{e_o - \micro e_g}}{{r_p}}}$ = $\displaystyle {\frac{{e_o + \micro e_o}}{{r_p}}}$ = $\displaystyle {\frac{{(1 + \micro)e_o}}{{r_p}}}$
Z_o	=	$\displaystyle {\frac{{e_o}}{{i_1 + i_2 + i_3}}}$ = $\displaystyle {\frac{{1}}{{\frac{1+\micro}{r_p} + \frac{1}{R_L} + \frac{1}{R_g}}}}$	(2.22)

負荷抵抗 R_L およびグリッド抵抗 R_g を除いた出力インピーダンス Z₁ は， μ $\gg$ 1 ならば，

Z₁ = $\displaystyle {\frac{{r_p}}{{1 + \micro}}}$ $\displaystyle \approx$ $\displaystyle {\frac{{r_p}}{{\micro}}}$ = $\displaystyle {\frac{{1}}{{g_m}}}$

(2.23)

と近似できます．

2.3.1 例1--固定バイアス1

プレート接地はさまざまな回路が考えられるので，それぞれについてシミュレーションを行ないます．交流増幅器になるので，入出力インピーダンスは入力や出力に交流電圧源を接続して，増幅回路に流れ込む電流を測定して求めます．入出力インピーダンスを同時に求めることはできないので，増幅回路をサブ回路として，2組の回路を構成し，一方で増幅度と入力インピーダンスを，もう一方で出力インピーダンスを求めます．

最初に，図2.10の 12AU7による固定バイアスのカソードフォロワを解析します．

**図 2.10:** プレート接地(シミュレーション用固定バイアス1)
$\begin{figure}\input{figs/com_p_1_spice} \end{figure}$

電源電圧 E_bb = 200 V, 負荷抵抗 R_L = 33 kΩ, グリッド抵抗 R_g = 100 kΩ とします．動作点は， E_p = 100 V, E_g = - 3.646829 V, I_p = 3.0303 mA で，この動作点における三定数は， g_m = 1513.786 μS, r_p = 11.34946 kΩ, μ = 17.18064 です．この回路の増幅度は式(2.18)，入力インピーダンスは式(2.20)，出力インピーダンスは式(2.22)を使って求めます．

A	=	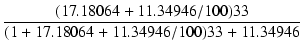$\displaystyle {\frac{{(17.18064 + 11.34946 / 100) 33}}{{(1 + 17.18064 + 11.34946 / 100) 33 + 11.34946}}}$ = 0.9278936
Z_i	=	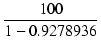$\displaystyle {\frac{{100}}{{1 - 0.9278936}}}$ = 1386.84 [kΩ]
Z_o	=	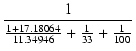$\displaystyle {\frac{{1}}{{\frac{1+17.18064}{11.34946}+\frac{1}{33}+\frac{1}{100}}}}$ = 0.6089398 [kΩ]

2.3.1.1 `com_p_1.cir`

    1 Common plate voltage amplifier (cathode follower) with 12AU7 (fixed bias 1)
    2 .INCLUDE 12AU7.lib
    3 .SUBCKT COMP1 IN OUT
    4 X1 4 2 3 12AU7
    5 RL 3 0 33k
    6 VBB 4 0 200V
    7 RG 2 1 100k
    8 VG 1 3 -3.64683V
    9 CI 2 IN 1u
   10 CO 3 OUT 1000u
   11 .ENDS
   12 
   13 XA1 1 2 COMP1
   14 VI 1 0 DC 0V AC 1V
   15 RL 2 0 100Meg
   16 
   17 XA2 3 4 COMP1
   18 VS 3 0 DC 0V
   19 VO 4 0 DC 0V AC 1V
   20 .control
   21 op
   22 print v(a1:4,a1:3) v(a1:2,a1:3) v:a1:bb#branch
   23 ac dec 1 1k 1k
   24 print abs(v(2)/v(1)) abs(v(1)/i(vi)) abs(v(4)/i(vo))
   25 .endc
   26 .END

3行目から11行目が，図2.10の点線で囲った部分をサブ回路としたもので， 13行目と17行目で使っています．

13行目からが増幅度と入力インピーダンスを求める回路で， 17行目からが出力インピーダンスを求める回路です．

22行目で動作点の各値を表示していますが，サブ回路の中のノードの値を表示するため，ノードの指定が複雑になっています．

2.3.1.2 結果

    1 
    2 Circuit: Common plate voltage amplifier (cathode follower) with 12AU7 (fixed bias 1)
    3 
    4 v(a1:4,a1:3) = 1.000000e+02
    5 v(a1:2,a1:3) = -3.64683e+00
    6 v:a1:bb#branch = -3.03030e-03
    7 abs(v(2)/v(1)) = 9.278865e-01
    8 abs(v(1)/i(vi)) = 1.386594e+06
    9 abs(v(4)/i(vo)) = 6.089417e+02

入力インピーダンスの差が少しありますが，インピーダンスがかなり高いため，真空管の電極間容量の影響が出ています．

2.3.2 例2--固定バイアス2

例1のグリッド抵抗およびバイアス電圧をカソードではなくアースに接続した回路(図2.11)を解析します． RCの定数，動作点，三定数は，前節の場合と同じです．

**図 2.11:** プレート接地(シミュレーション用固定バイアス2)
$\begin{figure}\input{figs/com_p_2_spice} \end{figure}$

この回路の増幅度は式(2.18)，出力インピーダンスは式(2.22)を使って求めますが， R_g = $\infty$ とします．また，入力インピーダンスは Z_i = R_g です．

A	=	$\displaystyle {\frac{{17.18064 \times 33}}{{(1 + 17.18064) 33 + 11.34946}}}$ = 0.9274518
Z_i	=	100 [kΩ]
Z_o	=	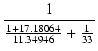$\displaystyle {\frac{{1}}{{\frac{1+17.18064}{11.34946}+\frac{1}{33}}}}$ = 0.6126705 [kΩ]

この回路の場合，カソード接地増幅回路に100%の負帰還をかけたものと解釈することができます．カソード接地の増幅度 | A_o| は，

| A_o| = μ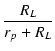 $\displaystyle {\frac{{R_L}}{{r_p + R_L}}}$

(2.24)

ですから，帰還後の増幅度 A_f は， $\beta$ = 1 なので，

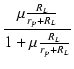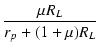
A_f = $\displaystyle {\frac{{A_o}}{{1+A_o}}}$ = $\displaystyle {\frac{{\micro \frac{R_L}{r_p+R_L}}}{{1+\micro \frac{R_L}{r_p+R_L}}}}$ = $\displaystyle {\frac{{\micro R_L}}{{r_p + (1+\micro)R_L}}}$

(2.25)

となり，式(2.18)に R_g = $\infty$ を代入したものと一致します．

2.3.2.1 `com_p_2.cir`

    1 Common plate voltage amplifier (cathode follower) with 12AU7 (fixed bias 2)
    2 .INCLUDE 12AU7.lib
    3 .SUBCKT COMP2 IN OUT
    4 X1 4 2 3 12AU7
    5 RL 3 0 33k
    6 VBB 4 0 200V
    7 RG 2 1 100k
    8 VG 1 0 96.35317V 
    9 CI 2 IN 1u
   10 CO 3 OUT 1000u
   11 .ENDS
   12 
   13 XA1 1 2 COMP2
   14 VI 1 0 DC 0V AC 1V
   15 RL 2 0 100Meg
   16 
   17 XA2 3 4 COMP2
   18 VS 3 0 DC 0V
   19 VO 4 0 DC 0V AC 1V
   20 .control
   21 op
   22 print v(a1:4,a1:3) v(a1:2,a1:3) v:a1:bb#branch
   23 ac dec 1 1k 1k
   24 print abs(v(2)/v(1)) abs(v(1)/i(vi)) abs(v(4)/i(vo))
   25 .endc
   26 .END

2.3.2.2 結果

    1 
    2 Circuit: Common plate voltage amplifier (cathode follower) with 12AU7 (fixed bias 2)
    3 
    4 v(a1:4,a1:3) = 1.000000e+02
    5 v(a1:2,a1:3) = -3.64683e+00
    6 v:a1:bb#branch = -3.03030e-03
    7 abs(v(2)/v(1)) = 9.274435e-01
    8 abs(v(1)/i(vi)) = 1.000002e+05
    9 abs(v(4)/i(vo)) = 6.126713e+02

2.3.3 例3--自己バイアス1

図2.7の自己バイアスの回路を解析します． RCの定数，動作点，三定数は，前節の場合と同じです．

**図 2.12:** プレート接地(シミュレーション用自己バイアス1)
$\begin{figure}\input{figs/com_p_3_spice} \end{figure}$

この回路の増幅度，入出力インピーダンスは，例1と同じです．

2.3.3.1 `com_p_3.cir`

    1 Common plate voltage amplifier (cathode follower) with 12AU7 (self bias 1)
    2 .INCLUDE 12AU7.lib
    3 .SUBCKT COMP3 IN OUT
    4 X1 4 2 3 12AU7
    5 RK 3 5 1203.454
    6 CK 3 5 1000u
    7 RL 5 0 33k
    8 VBB 4 0 203.64683V
    9 RG 2 5 100k
   10 CI 2 IN 1u
   11 CO 3 OUT 1000u
   12 .ENDS
   13 
   14 XA1 1 2 COMP3
   15 VI 1 0 DC 0V AC 1V
   16 RL 2 0 100Meg
   17 
   18 XA2 3 4 COMP3
   19 VS 3 0 DC 0V
   20 VO 4 0 DC 0V AC 1V
   21 .control
   22 op
   23 print v(a1:4,a1:3) v(a1:2,a1:3) v:a1:bb#branch
   24 ac dec 1 1k 1k
   25 print abs(v(2)/v(1)) abs(v(1)/i(vi)) abs(v(4)/i(vo))
   26 .endc
   27 .END

2.3.3.2 結果

    1 
    2 Circuit: Common plate voltage amplifier (cathode follower) with 12AU7 (self bias 1)
    3 
    4 v(a1:4,a1:3) = 1.000000e+02
    5 v(a1:2,a1:3) = -3.64683e+00
    6 v:a1:bb#branch = -3.03030e-03
    7 abs(v(2)/v(1)) = 9.278865e-01
    8 abs(v(1)/i(vi)) = 1.386595e+06
    9 abs(v(4)/i(vo)) = 6.089417e+02

2.3.4 例4--自己バイアス2

前節の回路のカソードバイパスコンデンサ CK を取り除き，負荷抵抗 RL とカソード抵抗 RK の和が 33 kΩ となるように調整します．また，電源電圧もバイアスの分だけ下げます．回路は図2.13のようになります．

**図 2.13:** プレート接地(シミュレーション用自己バイアス2)
$\begin{figure}\input{figs/com_p_4_spice} \end{figure}$

等価回路(略)より，

e_o	=	(i₁ + i₂)R_L + i₂R_k	(2.26)
μe_g	=	(i₁ + i₂)R_L + i₂(r_p + R_k)	(2.27)
e_i	=	(i₁ + i₂)R_L + i₁R_g	(2.28)
e_i	=	e_g + (i₁ + i₂)R_L	(2.29)

が成り立ち，これより，

e_g	=	e_i - e_o = e_i - (i₁ + i₂)R_L - i₂R_k
μe_i	=	(1 + μ)(i₁ + i₂)R_L + {(1 + μ)R_k + r_p}i₂
	=	(1 + μ)R_Li₁ + {r_p + (1 + μ)R_L + (1 + μ)R_k}i₂
e_i	=	(R_L + R_g)i₁ + R_Li₂
i₁	=	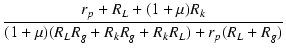$\displaystyle {\frac{{r_p+R_L+(1+\micro)R_k}}{{(1+\micro)(R_L R_g + R_k R_g + R_k R_L) + r_p(R_L + R_g)}}}$ e_i
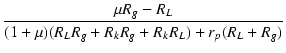i₂	=	$\displaystyle {\frac{{\micro R_g-R_L}}{{(1+\micro)(R_L R_g + R_k R_g + R_k R_L) + r_p(R_L + R_g)}}}$ e_i
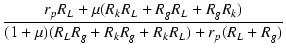e_o	=	$\displaystyle {\frac{{r_p R_L + \micro(R_k R_L + R_g R_L + R_g R_k)}}{{(1+\micro)(R_L R_g + R_k R_g + R_k R_L) + r_p(R_L + R_g)}}}$ e_i
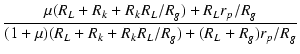	=	$\displaystyle {\frac{{\micro(R_L + R_k + R_k R_L/R_g) + R_L r_p/ R_g}}{{(1+\micro)(R_L + R_k + R_k R_L/R_g) + (R_L + R_g) r_p / R_g}}}$ e_i

この場合の増幅度 A，入力インピーダンス Z_i，出力インピーダンス Z_o は，

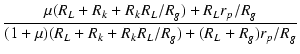A	=	$\displaystyle {\frac{{\micro(R_L + R_k + R_k R_L/R_g) + R_L r_p/ R_g}}{{(1+\micro)(R_L + R_k + R_k R_L/R_g) + (R_L + R_g) r_p / R_g}}}$	(2.30)
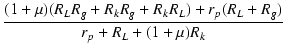Z_i	=	$\displaystyle {\frac{{e_i}}{{i_1}}}$ = $\displaystyle {\frac{{(1+\micro)(R_L R_g + R_k R_g + R_k R_L) + r_p(R_L + R_g)}}{{r_p+R_L+(1+\micro)R_k}}}$	(2.31)
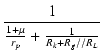Z_o	=	$\displaystyle {\frac{{1}}{{\frac{1+\micro}{r_p} + \frac{1}{R_k+R_g//R_L}}}}$	(2.32)

となります．したがって，この例の数値をあてはめると，

R'	=	R_L + R_k + R_kR_L/Rg = 31.79655 + 1.203454 + 1.203454 `x` 31.79655/100 = 33.38266 [kΩ]
A	=	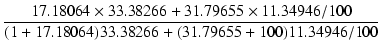$\displaystyle {\frac{{17.18064 \times 33.38266 + 31.79655 \times 11.34946 / 100}}{{(1 + 17.18064) 33.38266 + (31.79655 + 100) 11.34946 / 100}}}$ = 0.9280691
Z_i	=	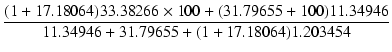$\displaystyle {\frac{{(1 + 17.18064) 33.38266 \times 100 + (31.79655 + 100) 11.34946}}{{11.34946 + 31.79655 + (1 + 17.18064) 1.203454}}}$ = 956.357 [kΩ]
Z_o	=	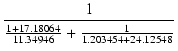$\displaystyle {\frac{{1}}{{\frac{1+17.18064}{11.34946}+\frac{1}{1.203454+24.12548}}}}$ = 0.6092449 [kΩ]

2.3.4.1 `com_p_4.cir`

    1 Common plate voltage amplifier (cathode follower) with 12AU7 (self bias 2)
    2 .INCLUDE 12AU7.lib
    3 .SUBCKT COMP4 IN OUT
    4 X1 4 2 3 12AU7
    5 RK 3 5 1203.454
    6 RL 5 0 31.79655k
    7 VBB 4 0 200V
    8 RG 2 5 100k
    9 CI 2 IN 1u
   10 CO 3 OUT 1000u
   11 .ENDS
   12 
   13 XA1 1 2 COMP4
   14 VI 1 0 DC 0V AC 1V
   15 RL 2 0 100Meg
   16 
   17 XA2 3 4 COMP4
   18 VS 3 0 DC 0V
   19 VO 4 0 DC 0V AC 1V
   20 .control
   21 op
   22 print v(a1:4,a1:3) v(a1:2,a1:3) v:a1:bb#branch
   23 ac dec 1 1k 1k
   24 print abs(v(2)/v(1)) abs(v(1)/i(vi)) abs(v(4)/i(vo))
   25 .endc
   26 .END

2.3.4.2 結果

    1 
    2 Circuit: Common plate voltage amplifier (cathode follower) with 12AU7 (self bias 2)
    3 
    4 v(a1:4,a1:3) = 1.000000e+02
    5 v(a1:2,a1:3) = -3.64683e+00
    6 v:a1:bb#branch = -3.03030e-03
    7 abs(v(2)/v(1)) = 9.280620e-01
    8 abs(v(1)/i(vi)) = 9.562632e+05
    9 abs(v(4)/i(vo)) = 6.092468e+02

Next: 2.4 グリッド接地 Up: 2. 電圧増幅回路 Previous: 2.2 電流帰還

Ayumi Nakabayashi
平成19年6月28日