 |
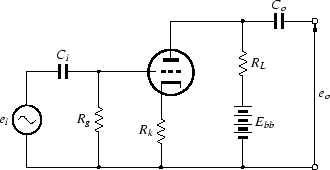
自己バイアスによるカソード接地回路のカソードバイパスコンデンサを取り除くと, カソードは交流的にアースされなくなり, 出力電圧の一部がカソードに現われます. この電圧は入力と同位相のため, G-K間に加わる信号は入力よりも小さくなり, 増幅度が下がります. カソード接地電流帰還増幅回路を図2.4に, その等価回路を図2.5に示します.
等価回路から,次の関係が導かれます.
| eo | = | - μeg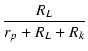 |
(2.5) |
| ek | = | μeg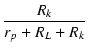 |
(2.6) |
| ei | = | eg + ek | (2.7) |
| r'p | = | rp + (1 + μ)Rk | (2.9) |
| Zi | = | Rg | (2.10) |
| Zo | = | r'p//RL | (2.11) |
| A | = | -17.20398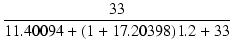 = - 8.570083 = - 8.570083 |
|
| Zi | = | 470 kΩ | |
| r'p | = | 11.40094 + (1 + 17.20398)1.2 = 33.24572 [kΩ] | |
| Zo | = | 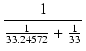 = 16.56120 [kΩ] = 16.56120 [kΩ] |
1 Common cathode voltage amplifier with current feedback (12AU7)
2 .INCLUDE 12AU7.lib
3 X1 1 2 3 12AU7
4 RL 1 4 33k
5 VBB 4 0 200V
6 RG 2 0 470k
7 VI 2 0 DC 0V AC 1V
8 RK 3 0 1.2k
9 .control
10 op
11 print v(1,3) v(2,3) i(vbb)
12 tf v(1) vi
13 print all
14 .endc
15 .END
1
2 Circuit: Common cathode voltage amplifier with current feedback (12AU7)
3
4 v(1,3) = 9.814915e+01
5 v(2,3) = -3.57371e+00
6 i(vbb) = -2.97810e-03
7 transfer_function = -8.57008e+00
8 output_impedance_at_v(1) = 1.656120e+04
9 vi#input_impedance = 4.700000e+05
| Ao| = μ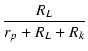
|
(2.12) |
Af = 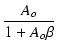 = = 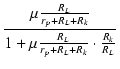 = μ = μ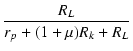
|
(2.13) |