


Next: 6.3 時定数が3段の場合の周波数特性
Up: 6. 負帰還(工事中)
Previous: 6.1 時定数が1段の場合の周波数特性
中域の利得を AM,
低域の時定数を TL1, TL2 とすると,
低域の利得 AL は次の式で表されます.
ここで,
x = 1/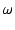 TL1,
n = TL2/TL1 とおくと,
TL1,
n = TL2/TL1 とおくと,
| AL |
= |
AM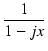 . . 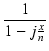 |
(6.3) |
| |
= |
AM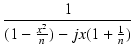 |
(6.4) |
負帰還率 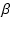 の負帰還をかけた場合,
低域の利得 A'Lは次の式のようになります.
の負帰還をかけた場合,
低域の利得 A'Lは次の式のようになります.
| A'L |
= |
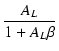 |
(6.5) |
| |
= |
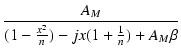 |
(6.6) |
| |
= |
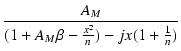 |
(6.7) |
中域の負帰還量を
1 + AM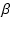 = FM とおくと,
= FM とおくと,
A'L = 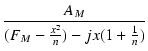
|
(6.8) |
となって,周波数特性の形状は,中域の利得 AM とは関係のないことがわかります.
利得の大きさ(絶対値)は,
| A'L| = AM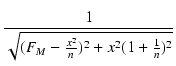
|
(6.9) |
X = x2 とおくと,式(6.9)の分母の根号の中は,
次のようになります.
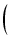 FM- FM-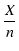 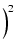 +X +X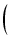 1+ 1+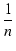 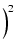 |
| |
= |
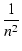 X2 + X2 + 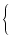 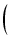 1 + 1 + 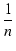 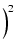 - - 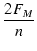 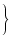 X + FM2 X + FM2 |
(6.11) |
| |
= |
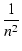 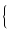 X2 + (n2 +2n + 1 - 2nFM)X + n2FM2 X2 + (n2 +2n + 1 - 2nFM)X + n2FM2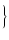 |
(6.12) |
| |
= |
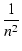 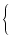 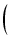 X - X - 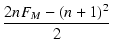 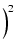 + n2FM2 - + n2FM2 - 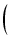 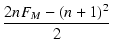 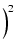 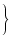 |
(6.13) |
| |
= |
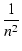 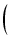 X - X - 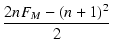 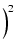 + + 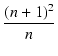 FM - FM - 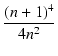 |
(6.14) |
したがって,分母が最小になる(すなわち | A'L| が最大になる)のは,
X = nFM - (n + 1)2/2 のとき(すなわち
x = xp 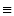
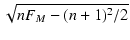 のとき)で,
このときの角周波数を
のとき)で,
このときの角周波数を 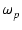 とすれば,
であり,
このときの利得 | A'Lp| は,
とすれば,
であり,
このときの利得 | A'Lp| は,
| A'Lp| = AM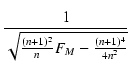
|
(6.16) |
となります.
中域の利得
A'M = AM/FM に対するこのピークの大きさ P は,
となります.
この根号の中が1以上であれば,ピークを生じることはありません.
N = (n + 1)2/n とおけば,この条件は,
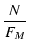 - - 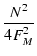 |
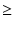 |
1 |
(6.18) |
NFM - 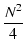 |
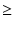 |
FM2 |
(6.19) |
FM2 - NFM + 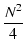 |
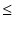 |
0 |
(6.20) |
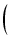 FM - FM - 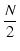 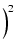 |
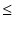 |
0 |
(6.21) |
| FM |
= |
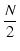 = = 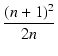 |
(6.22) |
帰還量がこれより少ない場合は,式(6.15)の根号の中が負になり,
ピークを生じないことになります.
図6.2に,スタガ比を1とした場合に,
負帰還量を変えた場合の利得と位相の周波数特性を示します.
ここで,スタガ比が n のとき,
ピークを P まで許容した場合に,どれだけの負帰還を掛けられるかを考えます.
式(6.17)を FM について解くと,
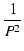 FM2 - FM2 - 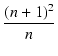 FM + FM + 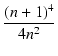 |
= |
0 |
(6.23) |
FM = 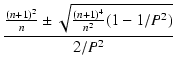 |
= |
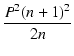 (1 (1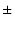 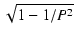 ) ) |
(6.24) |
符号が負の場合はピークが生じないので,解を与える符号は正です.
この関係をグラフで表すと,図6.3のようになります.
また,各種のスタガ比に対する帰還量とピークの位置の関係は,
図6.4, 6.5のようになります.
図 6.4:
帰還量とピークの位置(n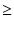 1)
1)
|
|
図 6.5:
帰還量とピークの位置(n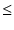 1)
1)
|
|
これらの図の使い方ですが,
たとえば,スタガ比を n = 1,
時定数を
TL1 = TL2 = 25 μF . k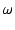 (ms),
負帰還量を F = 10 (
20 dB)とします.
このとき,図6.3より,ピークの大きさは
P = 4.44 dB となります.
また,図6.5より,ピークの位置は xp = 2.83 から,
(ms),
負帰還量を F = 10 (
20 dB)とします.
このとき,図6.3より,ピークの大きさは
P = 4.44 dB となります.
また,図6.5より,ピークの位置は xp = 2.83 から,
fp = 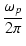 = = 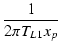 = 2.25 [Hz] = 2.25 [Hz]
|
(6.25) |
となります.
ここで,スタガ比を n = 10 として,
TL2 = 250 μF . kΩ とすると,
ピークの大きさは
P = 0.74 dB となり,
ピークの位置は,xp = 6.28 より
fp = 1.01 [Hz] となります.
ここで,スタガ比を n = 0.1 として,
TL2 = 2.5 μF . kΩ とすると,
ピークの大きさは同じく
P = 0.74 dB ですが,
ピークの位置は,xp = 0.628 より
fp = 10.1 [Hz] となります.
この3通りの場合の利得の周波数特性は,図6.6のようになります.
図 6.6:
各種スタガ比と周波数特性(F = 10)
|
|



Next: 6.3 時定数が3段の場合の周波数特性
Up: 6. 負帰還(工事中)
Previous: 6.1 時定数が1段の場合の周波数特性
Ayumi Nakabayashi
平成19年6月28日
 .
. 
 .
. 
 .
. 
 .
. 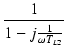
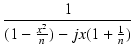
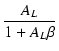
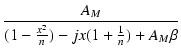
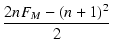
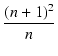 FM -
FM - 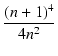
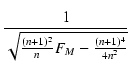
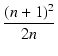
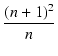 FM +
FM + 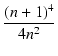
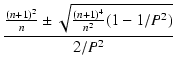
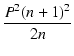 (1
(1![]() (ms),
負帰還量を F = 10 (
20 dB)とします.
このとき,図6.3より,ピークの大きさは
P = 4.44 dB となります.
また,図6.5より,ピークの位置は xp = 2.83 から,
(ms),
負帰還量を F = 10 (
20 dB)とします.
このとき,図6.3より,ピークの大きさは
P = 4.44 dB となります.
また,図6.5より,ピークの位置は xp = 2.83 から,
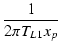 = 2.25 [Hz]
= 2.25 [Hz]