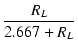


Next: B. 真空管のモデル
Up: A. 基礎知識
Previous: A.2 分圧,分流
電源と抵抗からなる2端子の回路があるとき、
その回路は、1つの電圧源と1つの抵抗からなる等価な回路で置き換えることができます。
電圧源の電圧は、2つの端子を開放したときの電圧で、
抵抗は、回路内の電圧源を短絡し、電流源を開放して測定した2端子間の抵抗になります(図A.6)。
図 A.6:
テブナンの定理
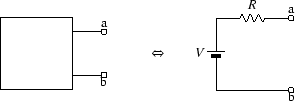 |
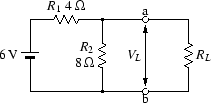
たとえば、電圧源と抵抗からなる図A.7の回路に、
任意の負荷を接続した場合のa-b間の電圧を知りたいとします。
図 A.7:
電圧源と抵抗からなる回路と負荷抵抗
 |
開放電圧 Vo は、
Vo =
V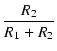
= 6
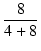
= 4 [
V]
となります。
電圧源を短絡したa-b間の抵抗 Ri は、
Ri =
R1//
R2 = 4//8 =
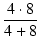
= 2.667 [Ω]
となります。
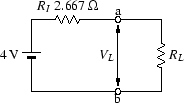
したがって、この回路は図A.8と等価であり、
任意の抵抗をa-b間に接続した場合のa-b間の電圧は、
VL =
Vo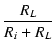
= 4
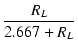
で求められることになります。
図 A.8:
テブナンの定理による等価回路
 |



Next: B. 真空管のモデル
Up: A. 基礎知識
Previous: A.2 分圧,分流
Ayumi Nakabayashi
平成19年6月28日
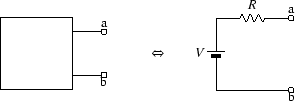
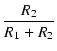 = 6
= 6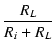 = 4
= 4