1.4 真空管による増幅と三定数

真空管は，実際には図1.3のような回路で使われることはありません． グリッド電圧の変化は，プレート電流の変化となりますが， 通常は，これを電圧の変化として取り出します． そのために，図1.8のように 電源 E_bb とプレートの間に負荷抵抗 R_L を入れ， プレート電圧の変化を出力とします．

図 1.8: 三極管による電圧増幅回路

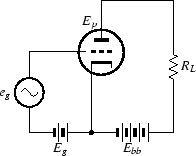
e_g は信号入力電圧で， E_g は e_g が加わった場合でも つねにグリッド電圧が負になるようにするための バイアス電圧(グリッドバイアス)です， グリッド電圧が負であれば，グリッドに電流は流れませんが， グリッド電圧が正になるとグリッド電流が流れだし， 入力インピーダンスが下がるため， 電圧増幅段ではグリッド電圧が常に負になるようにして使います．

さて，図1.8の回路で， プレート電流が I_p 流れたとき， プレート電圧 E_p は，電源電圧 E_bb から 負荷抵抗 R_L の電圧降下 I_pR_L を引いた電圧になります． すなわち，

E_p = E_bb - I_pR_L (1.11)

この，R_L によって定まるプレート電圧とプレート電流の関係を プレート特性に書き込むと，図1.9の直線のようになります． この直線を負荷抵抗線(ロードライン: load line)といいます． 図に示したように，ロードラインは (E_bb, 0) と (0, E_bb/R_L) を 通る直線です．

図 1.9: 静特性による増幅回路の解析

このように，負荷抵抗があると， プレートにかかる電圧はプレート電流によって変わってきます．

入力信号がない場合，グリッド電圧は E_g であり， そのグリッド電圧のプレート特性曲線とロードラインとの交点により プレート電圧とプレート電流が決まります． 図1.9ではA点です． この点を動作点といいます．

入力電圧が加わり，グリッド電圧が E_g + e_g になった場合， プレート特性曲線とロードラインとの交点はBになります． このとき，e_g > 0 なら，プレート電流は $\Delta$I_p だけ増加し， プレート電圧は $\Delta$E_p = e_p だけ下がります． この増幅回路の増幅度 A は，

$${\frac{{e_p}}{{e_g}}}$$ (1.12)

となります．

ここで，増幅度と三定数の関係を調べます． 増幅率 μ より，

$$\vec{{\rm CA}}$$ (1.13)

三角形BCDに注目すると，内部抵抗 r_p より，

$${\frac{{\vec{\rm CD}}}{{\vec{\rm DB}}}}$$ r_p =

$$\vec{{\rm CD}} \vec{{\rm DB}} \Delta$$ = (1.14)

三角形ABDに注目すると，負荷抵抗 R_L によるロードラインより，

$$\vec{{\rm DA}} \Delta$$ (1.15)

$\vec{{\rm CA}}$ = $\vec{{\rm CD}}$ + $\vec{{\rm DA}}$ より，

$$\Delta \Delta$$ μe_g =

$$\Delta$$ =

$$\Delta {\frac{{\micro e_g}}{{r_p + R_L}}}$$ = (1.16)

式(1.16)を式(1.15)に代入して，

$${\frac{{R_L}}{{r_p + R_L}}}$$ (1.17)

したがって，増幅度 A は，

$${\frac{{e_p}}{{e_g}}} {\frac{{R_L}}{{r_p + R_L}}}$$ (1.18)

となります．

さて，式(1.17)は，電圧 - μe_g を，r_p と R_L で 分圧していると見ることができます． 負荷抵抗 R_L の両端に生じる出力電圧は， 開放電圧が - μe_g で内部抵抗が r_p の電圧源に R_L をつないだ場合とまったく同じになります． これより図1.8の回路の信号成分の等価回路は 図1.10のように表せます．

図 1.10: 電圧源による等価回路

式(1.17)に， μ = g_mr_p を代入すると，

$${\frac{{r_p R_L}}{{r_p + R_L}}}$$ (1.19)

となり，r_p と R_L が並列になった回路に電流 - g_me_g を 流したときに生じる電圧が e_p になります． これは，内部抵抗が r_p の電流源と等価です． これより図1.8の回路の信号成分の等価回路は 図1.11のようにも表せます．

図 1.11: 電流源による等価回路