


Next: 1.4 真空管による増幅と三定数
Up: 1. 静特性と三定数
Previous: 1.2 三極管の静特性
1.3 三定数
三極管の場合,真空管の特性はプレート特性曲線にすべて現れています.
しかし,真空管回路の性質を解析する場合,
このような大量の情報を扱うのはやっかいです.
また,電力増幅段を除いては,
扱う信号の大きさはプレート電圧等にくらべてかなり小さいので,
特性曲線のごく小さい範囲の特性を近似的に表せれば十分といえます.
三極管では,以下に述べる3つの定数で,
ある点(図1.6では点Aとします)の特性を表します.
図 1.6:
プレート特性と三定数
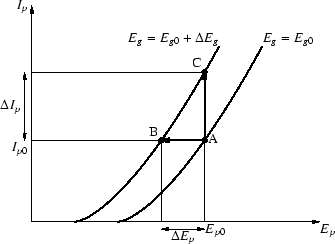 |
グリッド電圧を変化させたとき,
プレート電流を一定に保つようにするためには
プレート電圧を変えなければなりません.
このプレート電圧の変化をグリッド電圧の変化で割ったものが
増幅率(amplification factor)で,μ と表します.
実際には,グリッド電圧を上げたときにプレート電流を一定にするには
プレート電圧を下げなければならないので,
増幅率を正の値とするために,符号を逆にします.
式で表すと,次のようになります.
μ は電圧を電圧で割ったものなので,単位はありません.
オーディオに使われる三極管の場合,μ の値は2から100程度です.
プレート電圧を一定にして,
グリッド電圧を変化させたときに,どれだけプレート電流が変化するかを
表す量を相互コンダクタンス(transconductance)といい,gm で表します.
単位は,S (シーメンス
)です,以前は 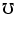 (モー)が使われていました.
相互コンダクタンスは非常に小さな値なので,
mS や μS がよく使われます.
(モー)が使われていました.
相互コンダクタンスは非常に小さな値なので,
mS や μS がよく使われます.
グリッド電圧を一定にして,
プレート電圧を変化させたとき,プレート電流がどれだけ変化するかを
表す量をプレート抵抗(plate registance)といい,rp で表します.
単位は Ω です.
プレート抵抗は内部抵抗ともいいます.
プレート特性曲線上で,
各グリッド電圧の曲線が立っているものほどプレート抵抗が低く,
曲線が寝ているものほどプレート抵抗が高くなります.
式(1.3), (1.4)より,
という関係が成り立ちます.
したがって,三定数のうち2つが分かれば,残りの定数を知ることができます.
プレート電流は,グリッド電圧とプレート電圧の関数であるといえます.
すなわち,
Ip = f (Eg, Ep)
この場合,プレート電流の変化は,
2次の項を無視すれば次の式で表されます.
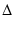 Ip Ip |
= |
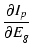 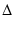 Eg + Eg + 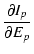 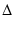 Ep Ep |
(1.6) |
| |
= |
gm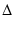 Eg + Eg + 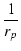 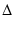 Ep Ep |
|
増幅率の定義より,μ は
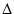 Ip が0となるような
Ip が0となるような
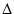 Ep と
Ep と
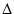 Eg の比率のことです.
Eg の比率のことです.
gm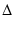 Eg + Eg + 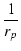 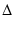 Ep Ep |
= |
0 |
|
gmrp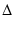 Eg Eg |
= |
- 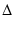 Ep Ep |
|
| gmrp |
= |
- 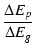 = μ = μ |
(1.7) |
ここでは,12AU7を例にとりあげ,
プレート特性図(図1.7)から三定数を求めてみます.
図 1.7:
12AU7のプレート特性から三定数を求める
|
|
データシートには,
Ep = 250 V,
Eg = - 8.5 V のとき,
μ = 17,
rp = 7700 Ω,
gm = 2200 μS という値が載っているので,
これを確かめます.
グラフから,
Ip = 10.5329 mA と読みとれます.
Rを使ってモデル(付録B)からこの値を求めるには,
次のように入力します.
> Ip(t12AU7, 250, -8.5)
[1] 0.01053290 # 単位はA
この点をAとします.
グリッド電圧を
Eg = - 8.5 V から
-7.5 V に変化させても,
プレート電流が
Ip = 10.5329 mA のまま変わらないプレート電圧を求めます.
> uniroot(function(x) Ip(t12AU7, x, -7.5) - 10.5329e-3, c(200, 250))$root
[1] 232.9815 # プレート電圧が200から250Vの間で探索
この点は図のBです.
これより,増幅率 μ は,
μ = 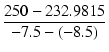 = 17.0185 = 17.0185
|
(1.8) |
と計算できます.
次に,プレート電圧を
Ep = 250 V のまま,
グリッド電圧を
Eg = - 7.5 V に変えてプレート電流を求めます.
> Ip(t12AU7, 250, -7.5)
[1] 0.01289177
この点はCです.
相互コンダクタンス gm は,
gm = 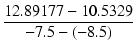 = 2.35887 mS = 2.35887 mS
|
(1.9) |
となります.
点Bと点Cから,内部抵抗 rp を求めます.
rp = 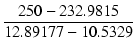 = 7.214683 kΩ = 7.214683 kΩ
|
(1.10) |
ちなみに,モデルで計算した三定数は,
> mu(t12AU7, 250, -8.5)
[1] 16.91149
> gm(t12AU7, 250, -8.5)
[1] 0.002221544 # 単位はS(シーメンス)
> rp(t12AU7, 250, -8.5)
[1] 7612.495 # 単位はΩ
となりますが,プレート特性図から求めた値は,
グリッド電圧の変化として
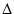 Eg = 1 V というかなり大きな値を使ったので,
正確な値と違ってきたのです.
Eg = 1 V というかなり大きな値を使ったので,
正確な値と違ってきたのです.
 Eg = 0.01 V 程度にすると,4桁近くまでモデルの値と合います.
Eg = 0.01 V 程度にすると,4桁近くまでモデルの値と合います.



Next: 1.4 真空管による増幅と三定数
Up: 1. 静特性と三定数
Previous: 1.2 三極管の静特性
Ayumi Nakabayashi
平成19年6月28日

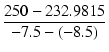 = 17.0185
= 17.0185
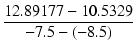 = 2.35887 mS
= 2.35887 mS
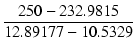 = 7.214683 kΩ
= 7.214683 kΩ