2.4 ダンピングファクター

ダンピングファクター $\it DF$ は，規定の負荷を R_L ，アンプの出力インピーダンスを Z_o とすると，次の式で定義されます．

$\displaystyle \it DF$ = $\displaystyle {\frac{{R_L}}{{Z_o}}}$

(2.34)

2.4.1 出力インピーダンスの測定法

2.4.1.1 ON-OFF法(その1)

負荷開放時の出力電圧 e_o と，規定負荷時の出力電圧 e_l を測定して，出力インピーダンスを求めます．

**図 2.24:** ON-OFF法の等価回路(その1)
$\begin{figure}\input{figs/df_onoff1} \end{figure}$

負荷開放時と規定負荷時の等価回路は，図2.24のようになるので，

e_o	=	e	(2.35)
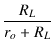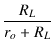e_l	=	e $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$	(2.36)

という関係が成り立ちます．ここから e を消去し，r_o について解くと，

e_l	=	e_o $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$
(r_o + R_L)e_l	=	e_oR_L
r_oe_l	=	(e_o - e_l)R_L
r_o	=	$\displaystyle {\frac{{e_o - e_l}}{{e_l}}}$ R_L	(2.37)

となり，この式により出力インピーダンスを求めることができます．

注意としては，多極管の無帰還アンプの場合，負荷開放にすると非常に高い電圧が発生するので，負荷開放時に歪まないようにレベルを調整します．

2.4.1.2 ON-OFF法(その2)

上述のように，多極管の無帰還アンプの場合は，負荷開放時と規定負荷時で出力が大きく変わってしまいます．そこで，8 Ω と 4 Ω ，あるいは 8 Ω と 16 Ω のように2種類の負荷で出力電圧を測定し，その値から出力インピーダンスを求めます．等価回路は，図2.25のようになります．

**図 2.25:** ON-OFF法の等価回路(その2)
$\begin{figure}\input{figs/df_onoff2} \end{figure}$

等価回路より，

e₁	=	e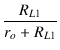 $\displaystyle {\frac{{R_{L1}}}{{r_o+R_{L1}}}}$	(2.38)
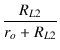e₂	=	e $\displaystyle {\frac{{R_{L2}}}{{r_o+R_{L2}}}}$	(2.39)

という関係が成り立つので， e を消去し，r_o について解くと，

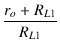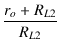e₁ $\displaystyle {\frac{{r_o+R_{L1}}}{{R_{L1}}}}$	=	e₂ $\displaystyle {\frac{{r_o+R_{L2}}}{{R_{L2}}}}$
e₁R_L2r_o + e₁R_L1R_L2	=	e₂R_L1r_o + e₂R_L1R_L2
(e₁R_L2 - e₂R_L1)r_o	=	(e₂ - e₁)R_L1R_L2
r_o	=	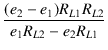$\displaystyle {\frac{{(e_2 - e_1) R_{L1} R_{L2}}}{{e_1 R_{L2} - e_2 R_{L1}}}}$
	=	$\displaystyle {\frac{{e_2 - e_1}}{{e_1/R_{L1} - e_2/R_{L2}}}}$	(2.40)

となり，この式により出力インピーダンスを求めることができます．

数値例で確認します． 8 Ω の負荷に対して 1.25V の出力が測定され， 16 Ω の負荷に対して 2V の出力が測定されたとします．この場合，

R_L1	=	8
R_L2	=	16
e₁	=	1.25
e₂	=	2

ですから，

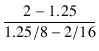r_o = $\displaystyle {\frac{{e_2 - e_1}}{{e_1/R_{L1} - e_2/R_{L2}}}}$ = $\displaystyle {\frac{{2 - 1.25}}{{1.25/8 - 2/16}}}$ = 24 [Ω]

と計算できます．

2.4.1.3 注入法

被試験アンプの出力インピーダンスが非常に低いと， ON-OFF法では測定値の差が小さくなり，測定不能となります．こういった場合は，別のアンプから信号を注入して，被試験アンプに流れ込んだ電流と，被試験アンプの出力端子の電圧を測定して出力インピーダンスを求めます．

**図 2.26:** 注入法による出力インピーダンスの測定
$\begin{figure}\input{figs/df_ins} \end{figure}$

信号注入アンプの出力インピーダンスが十分に低い場合は，図2.26(a)のように接続します． R_L は被試験アンプの規定負荷インピーダンスとします．この場合，被試験アンプに流れる電流 i は，

i = $\displaystyle {\frac{{e_2}}{{R_L}}}$

(2.41)

となるので，出力インピーダンス Z_o は，

Z_o = $\displaystyle {\frac{{e_1}}{{i}}}$ = $\displaystyle {\frac{{e_1}}{{e_2}}}$ R_L

(2.42)

となります．

信号注入アンプの出力インピーダンスが高い場合は，図2.26(b)のように接続します．ここで，r₃ は信号注入アンプの出力インピーダンスです． R₁ , R₂ の値は，被試験アンプの規定負荷インピーダンスを R_L とすれば，

R₁ + (R₂//r₃) = R_L

(2.43)

となるように選びます．被試験アンプに流れる電流 i は，

i = $\displaystyle {\frac{{e_2}}{{R_1}}}$

(2.44)

となるので，出力インピーダンス Z_o は，

Z_o = $\displaystyle {\frac{{e_1}}{{i}}}$ = $\displaystyle {\frac{{e_1}}{{e_2}}}$ R₁

(2.45)

となります．

2.4.2 負帰還とダンピングファクター

出力インピーダンスが r_o で，無負荷時のゲインが A のアンプを考えます(図2.27)．

**図 2.27:** 出力インピーダンスを持つアンプの等価回路
$\begin{figure}\input{figs/df_1} \end{figure}$

規定の負荷 R_L をかけた時のゲイン A_L は，

A_L = A $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$

(2.46)

となります．パワーアンプでは，通常この値をゲインと呼んでいます．

この例の場合，出力インピーダンスが r_o なので，ダンピングファクターは，

$\displaystyle \it DF$ = $\displaystyle {\frac{{R_L}}{{r_o}}}$

(2.47)

となります．

2.4.2.1 負帰還をかけた場合のゲイン

**図 2.28:** 負帰還をかけたときのゲイン
$\begin{figure}\input{figs/df_2} \end{figure}$

次に，出力の $\beta$ 倍の帰還をかけます．このとき，図より，

e_o = Ae_d = A(e_i - $\displaystyle \beta$ e_o)

(2.48)

が成り立ち，これを e_o について解くと，

e_o	=	Ae_i - A $\displaystyle \beta$ e_o
(1 + A $\displaystyle \beta$ )e_o	=	Ae_i
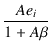e_o	=	$\displaystyle {\frac{{A e_i}}{{1 + A\beta}}}$	(2.49)

が得られ，無負荷時のゲイン A_f は，

A_f = $\displaystyle {\frac{{A}}{{1+A\beta}}}$ = $\displaystyle {\frac{{A}}{{F}}}$

(2.50)

となります．ここで，

F = 1 + A $\displaystyle \beta$

(2.51)

です．この F は真の意味での負帰還量なのですが，パワーアンプの場合は，この値を負帰還量とは呼ばず，規定の負荷をかけた場合のゲインの減少分を負帰還量と呼んでいます．

この状態で，規定の負荷をかけると，図より，

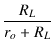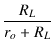e_o = Ae_d $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$ = A(e_i - $\displaystyle \beta$ e_o) $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$ = A_L(e_i - $\displaystyle \beta$ e_o)

(2.52)

という関係が成り立ち，これを e_o について解くと，

e_o	=	A_Le_i - A_L $\displaystyle \beta$ e_o
(1 + A_L $\displaystyle \beta$ )e_o	=	A_Le_i
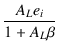e_o	=	$\displaystyle {\frac{{A_L e_i}}{{1 + A_L \beta}}}$	(2.53)

が得られ，負荷時のゲイン A_fL は，

A_fL = $\displaystyle {\frac{{A_L}}{{1 + A_L \beta}}}$

(2.54)

となります．

このゲインから，パワーアンプにおける通常の意味での負帰還量 F_L を求めると，

F_L = $\displaystyle {\frac{{A_L}}{{A_{fL}}}}$ = 1 + A_L $\displaystyle \beta$

(2.55)

となり，負荷を掛けたときの無帰還時のゲイン A_L と帰還率 $\beta$ を用いて，無負荷時と同様な式で算出されることがわかります．つまり，負帰還本来の定義から言えば，所定の帰還量となる $\beta$ を求めるためには，無負荷時のゲインが必要なのですが，負荷時に所定の帰還量となる $\beta$ を求めるのに，負荷時のゲインのみを考えればよいことになります．

2.4.2.2 負帰還をかけた場合の出力インピーダンス

負帰還後の出力インピーダンスは，入力端子をグラウンドに落とし，出力端子に e の電圧を加え，流れ込んだ電流 i から，

Z_o = $\displaystyle {\frac{{e}}{{i}}}$

(2.56)

で求めます．等価回路は，図2.29のようになります．

**図 2.29:** 負帰還をかけたときの出力インピーダンスを求める等価回路
$\begin{figure}\input{figs/df_3} \end{figure}$

r_o の両端の電圧は， (1 + A $\beta$ )e ですから，出力端子から流れ込む電流 i は，

i = 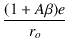$\displaystyle {\frac{{(1 + A\beta)e}}{{r_o}}}$

(2.57)

で，出力インピーダンス r_of は，

r_of = $\displaystyle {\frac{{e}}{{i}}}$ = $\displaystyle {\frac{{e}}{{\frac{(1 + A\beta)e}{r_o}}}}$ = $\displaystyle {\frac{{r_o}}{{1 + A\beta}}}$ = $\displaystyle {\frac{{r_o}}{{F}}}$

(2.58)

となります．したがって，出力インピーダンスは，真の負帰還量 F だけ改善されます．

この出力インピーダンスを用いて，規定負荷に対する負帰還アンプのゲインを求めてみましょう．無負荷時の負帰還アンプのゲインは式(2.50)で表され，出力インピーダンスは式(2.58)となるので，負荷時のゲインは，

A_fL	=	A_f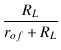 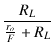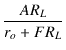$\displaystyle {\frac{{R_L}}{{r_{of}+R_L}}}$ = $\displaystyle {\frac{{A}}{{F}}}$ ^. $\displaystyle {\frac{{R_L}}{{\frac{r_o}{F}+R_L}}}$ = $\displaystyle {\frac{{A R_L}}{{r_o+F R_L}}}$
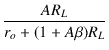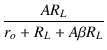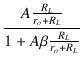	=	$\displaystyle {\frac{{A R_L}}{{r_o+ (1 + A\beta) R_L}}}$ = $\displaystyle {\frac{{A R_L}}{{r_o + R_L + A\beta R_L}}}$ = $\displaystyle {\frac{{A \frac{R_L}{r_o+R_L}}}{{1 + A\beta \frac{R_L}{r_o+R_L}}}}$
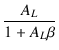	=	$\displaystyle {\frac{{A_L}}{{1 + A_L \beta}}}$	(2.59)

となって，式(2.54)と一致します．

2.4.2.3 ダンピングファクターの変化

帰還後のダンピングファクターは，

$\displaystyle \it DF_{f}^{}$ = $\displaystyle {\frac{{R_L}}{{r_{of}}}}$ = $\displaystyle {\frac{{R_L}}{{\frac{r_o}{F}}}}$ = F $\displaystyle {\frac{{R_L}}{{r_o}}}$ = F^. $\displaystyle \it DF$

(2.60)

となり，帰還前の F 倍になります．これをパワーアンプにおける通常の意味での負帰還量 F_L で表します．

式(2.55)に，式(2.46)を代入して，A $\beta$ について解くと，

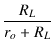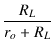F_L	=	1 + A $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$ $\displaystyle \beta$
A $\displaystyle \beta$ $\displaystyle {\frac{{R_L}}{{r_o+R_L}}}$	=	F_L - 1
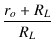A $\displaystyle \beta$	=	(F_L -1) $\displaystyle {\frac{{r_o+R_L}}{{R_L}}}$ = (F_L -1)^. $\displaystyle \Bigl($ $\displaystyle {\frac{{r_o}}{{R_L}}}$ +1 $\displaystyle \Bigr)$
	=	(F_L -1)^. $\displaystyle \Bigl($ $\displaystyle {\frac{{1}}{{\it DF}}}$ +1 $\displaystyle \Bigr)$	(2.61)

が得られ，これを式(2.51)に代入すると，

F	=	1 + (F_L -1)^. $\displaystyle \Bigl($ $\displaystyle {\frac{{1}}{{\it DF}}}$ +1 $\displaystyle \Bigr)$
	=	F_L $\displaystyle \Bigl($ $\displaystyle {\frac{{1}}{{\it DF}}}$ +1 $\displaystyle \Bigr)$ - $\displaystyle {\frac{{1}}{{\it DF}}}$	(2.62)

となり，負帰還後のダンピングファクターは，

$\displaystyle \it DF_{f}^{}$ = F^. $\displaystyle \it DF$ = F_L(1 + $\displaystyle \it DF$ ) - 1

(2.63)

となります．

つまり，ダンピングファクターは，真の負帰還量(F )だけ改善されますが，真の負帰還量を求めなくても，式(2.63)によって負帰還後のダンピングファクターを求めることができます．

2.4.2.4 数値例

ここで数値例をあげましょう． 8 Ω の負荷を掛けたときゲインが10倍で，ダンピングファクターが0.1のアンプがあったとします．すなわち，

A_L	=	10
$\displaystyle \it DF$	=	$\displaystyle {\frac{{8}}{{r_o}}}$ = 0.1

これより，内部抵抗は，

r_o = 80 [Ω]

となります．無負荷時のゲインは，式(2.46)を A について解いて，

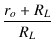A = A_L $\displaystyle {\frac{{r_o+R_L}}{{R_L}}}$ = 10 $\displaystyle {\frac{{80 + 8}}{{8}}}$ = 110

です．

このアンプに 6 dB の負帰還を掛けます．真の負帰還量は，式(2.62)より，

F = F_L $\displaystyle \Bigl($ $\displaystyle {\frac{{1}}{{\it DF}}}$ +1 $\displaystyle \Bigr)$ - $\displaystyle {\frac{{1}}{{\it DF}}}$ = 2(10 + 1) - 10 = 12

(21.6dB)となり，ダンピングファクターは12倍改善されて，1.2となります．式(2.63)から負帰還後のダンピングファクターを求めると，

$\displaystyle \it DF_{f}^{}$ = F_L(1 + $\displaystyle \it DF$ ) - 1 = 2(1 + 0.1) - 1 = 1.2

となり，一致します．

ayumi
2016-03-07