Next: 2.6 Rのプログラム Up: 2. シングル出力段 Previous: 2.4 ダンピングファクター
第2.1.4節で, 「信号入力時の平均プレート電流 Ipavg は, 無信号時のプレート電流 Ip0 と比べて, 第2高調波の波高値 h2 だけ増加します」と書きましたが, これは,信号を入れた直後の状態について述べたものであり, 時間が経過すると,出力トランスやカソードバイパスコンデンサの時定数により, プレート電流の平均値は複雑なふるまいをします.
第2.2節の2A3シングルを例にします.
図2.14からわかるように, 1サイクルの平均プレート電圧は,243.2V で, これは無信号時のプレート電圧 Ep0 = 250 V よりも低くなっています. この点は,図2.30の点Xです.
プレート電圧の平均値は, 出力トランスのインダクタンスの働きにより, 電源電圧の 250V に戻ろうとします. その結果,動作点はO'に移り, プレート電圧とプレート電流の平均値はX'になります. 平均プレート電圧は 249.1V となっていますが, この例の場合,出力トランスの一次巻線抵抗を 100 Ω としており, プレート電流の増分 69.4 - 60.0 = 9.4 mA の分だけプレート電圧が下がるからです.
これをシミュレーションで確かめてみましょう.
回路は,図2.31のようになります.
TX1は理想トランスであり,巻線抵抗がないので,R1を加えています.
一次インピーダンスを
2.5 kΩ
にするため,
巻数比は巻線抵抗を引いた
![]() :
: ![]() = 1 : 0.05773503
とします.
= 1 : 0.05773503
とします.
プレート電圧(VP)およびプレート電流(IP)の波形は, 図2.32のようになります.
プレート電流が増える時定数は,|
T = |
(2.64) |
プレート電流の増分を求めます(図2.34).
Xは,動作点がOのときの信号入力時の平均プレート電圧・電流の点で, 平均プレート電流と動作点の電流の差|
|
(2.65) |
|
|
(2.66) |
プレート電圧の平均値は,
無信号時のプレート電圧に戻ろうとします.
出力トランスの巻線抵抗を無視すれば,
X'はOを通る垂線上に来ます.
一方,グリッドバイアスは変化しないので,
信号入力時の動作点O'は,
Eg = Eg0
の特性曲線上にあります.
OとXの差と,O'とX'の差はほぼ等しいとみなせますから,
| BX' | = | (2.67) | |
| BO' | = | (2.68) | |
| OB | = | 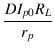 |
(2.69) |
|
|
(2.70) |
この例の場合は,歪率を5%とすれば,
となります.
シミュレーションの回路は,図2.36のようになります. プレート電圧,プレート電流の変化は,図2.37に示したように, いったんプレート電流が増えた後,定常状態に向けて電流が減っていきます.
定常状態になった後のプレート電圧および電流の平均値は, 図2.38のとおりで, 図2.35に示した値とほぼ一致しています.
なお,自己バイアスの場合は,最大出力時にバイアスが深くなるため, グリッド電圧が 0V に達するには, 当初のバイアスよりも大きな入力電圧を加えることになります. 一般に,メーカーのデータシートに記載されている入力電圧は, 連続最大出力時のものです. 今回の2A3の場合は, -45.04 V まで入力を加えることができ, 多少,出力が増えます.
プレート電流の増分を求めます(図2.39).
Xは,動作点Oに対応した信号入力時の平均プレート電圧・電流の点で, 平均プレート電流と動作点の電流の差|
|
(2.71) |
|
|
(2.72) |
平均プレート電流が増えることにより,
バイアスが深くなり,プレート電流を減らそうとします.
また,時間の経過とともに,プレート電圧の平均値は
カソード抵抗による直流ロードラインOX'上に戻ります.
平衡状態では,動作点がO'に移動し,
そのときのプレート電圧・電流の平均値はX'となります.
このときの静止時のプレート電流からの増分を
![]() Ip
とすると,
グリッド電圧の変化は
Ip
とすると,
グリッド電圧の変化は
![]() Eg = -
Eg = - ![]() IpRk
で,
プレート供給電圧もこの分だけ下がります.
OとXの差と,O'とX'の差はほぼ変わらないと見なせるので,
IpRk
で,
プレート供給電圧もこの分だけ下がります.
OとXの差と,O'とX'の差はほぼ変わらないと見なせるので,
| BO' | = | (2.73) | |
| BX' | = | (2.74) |
|
OD = - |
(2.75) |
| CD | = | - (1 + |
(2.76) |
| O'C | = | (2.77) |
| rp | = | ||
| = | 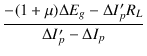 |
||
| = | (1 + |
||
| {rp + (1 + |
= | (rp + RL) |
|
| = | 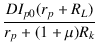 |
(2.78) |
この例の場合は,歪率を5%とすれば,
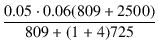 = 2.24 [mA]
= 2.24 [mA]
となります.
シミュレーションの回路は,図2.40です.
電圧制御電圧源E1が電圧増幅段のゲインを表しています.
R2とC2は位相補償の目的で入れています.
E2は位相補償用の素子の特性を乱さないためのバッファです.
![]() 回路はR3とR4で構成されており,
約 20dB の負帰還がかかっています.
回路はR3とR4で構成されており,
約 20dB の負帰還がかかっています.
各部の電圧,電流は,図2.41のようになります.
グリッド電圧の波形は,図2.42のように, 最大値が -0.19 V ,最小値が -91.29 V , 平均値が -43.5 V です.
負帰還により,プレート電圧やプレート電流の波形が正弦波になるよう, グリッド電圧の波形は負側に伸びた,2次歪みを含んだものになります.
波形より,基本波および第二次高調波の振幅を求めます.
式(2.15)および
式(2.20)を使います.
| f | = | 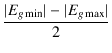 = = 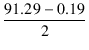 = 45.55 [V] = 45.55 [V] |
(2.79) |
| h2 | = | 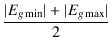 - | Egavg| = - | Egavg| = 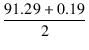 -43.5 = 2.24 [V] -43.5 = 2.24 [V] |
(2.80) |
|
D = |
(2.81) |
プレート特性図上で,この変化を表したものが, 図2.43です. 上記の計算は,2次歪みのみを考えていますので, シミュレーションの数値とは必ずしも一致しません.
動作点はX'に移ります. Y'は信号入力時の平均グリッド電圧に対するプレート電流です(あまり意味はありません). 負帰還によりグリッド電圧が低い部分(B')まで使っているので, 無帰還時と比べて出力が増えます. さらに,グリッド電圧が2次歪みを持つことにより, グリッドバイアスが浅くなるので,プレート電流が増え, 最小プレート電流がそれほど小さくならず, 無信号時のプレート電流をもう少し絞ることができそうです. ただし,あまりプレート電流を絞りすぎると, いきなりフルスイングしたときにカットオフしてしまうので, この場合でしたら 5mA 程度絞るのが限界です.
プレート電流の増分を求めます(図2.44).
動作点がOのときに,フルスイングした場合のグリッド電圧の平均値は Eg0 +|
|
(2.82) |
この例の場合,歪率は約5%で,グリッドバイアスが -43.5 V , gm = 4980 mS ですから, プレート電流の増分は,
|
|
(2.83) |
シミュレーションの回路は, 図2.45です.
各部の電圧,電流は,図2.46のようになります.
グリッド電圧の波形は,図2.47のように, 最大値が -1.03 V ,最小値が -94.79 V , 平均値が -45.17 V です.
グリッド電圧の波形より,基本波および第二次高調波の振幅を求めます.
| f | = | 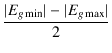 = = 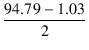 = 46.88 [V] = 46.88 [V] |
(2.84) |
| h2 | = | 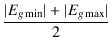 - | Egavg| = - | Egavg| = 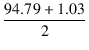 -45.17 = 2.74 [V] -45.17 = 2.74 [V] |
(2.85) |
|
D = |
(2.86) |
プレート特性図上で,この変化を表したものが, 図2.48です. 上記の計算は,2次歪みのみを考えていますので, シミュレーションの数値とは必ずしも一致しません.
プレート電流が 60mA から 62.31mA に増えることにより, バイアスが - 43.5V から -0.06231 x 725 = - 45.17 V になります. これがグリッド電圧の平均となるように, 位相0におけるグリッド電圧は,- 42.57V になります.
プレート電流の増分
![]() Ip
を求めます(図2.49).
Ip
を求めます(図2.49).
静止時の動作点Oに信号を加えると,
平均のグリッド電圧は
Eg0 + ![]() Eg'
となります(点Y).
グリッド電圧の変化分は,グリッドバイアス Eg0
と歪率 D
から求められ,
Eg'
となります(点Y).
グリッド電圧の変化分は,グリッドバイアス Eg0
と歪率 D
から求められ,
|
|
(2.87) |
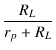
|
(2.88) |
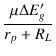
|
(2.89) |
時間が経過すると,グリッド電圧の平均値は当初の電圧 Eg0
に戻ろうとしますが,
グリッド電圧が上昇するため,プレート電流が増加します.
プレート電流が増加するとグリッドバイアスが深くなるため,
グリッド電圧が
Eg0 + ![]() Eg
のところで平衡します.
このとき,プレート電圧と電流の平均値はX'となり,
グリッド電圧の平均値の点はY'となります.
このX'とY'の電圧と電流の差は,
静止時のOとYの差と等しいと見なせますから,
Eg
のところで平衡します.
このとき,プレート電圧と電流の平均値はX'となり,
グリッド電圧の平均値の点はY'となります.
このX'とY'の電圧と電流の差は,
静止時のOとYの差と等しいと見なせますから,
| BY' | = | (2.90) | |
| BX' | = | (2.91) |
|
OD = - |
(2.92) |
| CD | = | AO + OD - BY' | |
| = | - 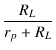 |
||
| Y'C | = | ||
| rp | = | 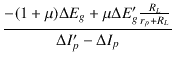 |
|
| = | (1 + 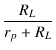 |
||
| {rp + (1 + |
= | - 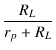 - - |
|
| = | 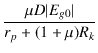 |
(2.93) |
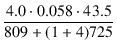 = 2.28 [mA]
= 2.28 [mA]
となり,シミュレーションの結果とほぼ一致します.
ayumi