Next: 2.2 三極管シングル出力段 Up: 2. シングル出力段 Previous: 2. シングル出力段
電力増幅回路では,真空管やトランジスタなどの能動素子の定格を超えない範囲で,
真空管を用いた場合,関連する定格は,
最大グリッド電圧の定格は,真空管を深くカットオフさせる用途,たとえばテレビの偏向出力や,C級出力段のために定められたものであり, オーディオ用途では,この定格を超えることはまず考えられません.
最大プレート電圧や最大プレート電流の尖頭定格が示されていない場合は, それぞれ平均値の定格の2倍が適用されます. すなわち,平均値による定格の範囲内に動作点があれば, 尖頭定格を気にする必要はありません. ただし,深いB級プッシュプルやOTLの場合では,平均値に比べ尖頭プレート電流が大きくなることもあります.
一般に,最初に定格に達するのはプレート損失なので, プレート損失に注目して設計を進め, 設計が終わった段階で,プレート電圧や電流の定格を超えていないかチェックすれば十分でしょう.
図2.2に,シングル出力段の回路図を示します. 左側が固定バイアスで,右側が自己バイアスです.
第1.2節でみたように, 出力トランスのインピーダンスは中域では抵抗分のみになり, その値はトランスの公称インピーダンス Zp と等しくなります. したがって,交流ロードラインはトランスの公称インピーダンスとなります.
一方,直流のロードラインは,トランスの一次巻線抵抗分になります.
具体的な例で見ていきましょう. 6EM7の第2ユニットを使い,動作点を Ep0 = 200 V , Ip0 = 50 mA とし,負荷インピーダンスを Zp = 2.5 kΩ とします. また,出力トランスの一次巻線抵抗を r1 = 146.8 Ω とします. プレート特性とロードラインは,図2.3のようになります.
プレート電圧が Ep0 = 200 V になるためには, トランスの巻線抵抗で
の電圧降下が起こるので,供給電圧を Ebb = 207.3 V とする必要があります. これは図の``C''点です.
さて, Ep0 = 200 V , Ip0 = 50 mA となるグリッド電圧は Eg0 = - 29.5 V です. グリッド電流が流れない範囲で正負対称な信号を加えると, グリッド電圧は,0 V から -29.5 x 2 = - 59 V の範囲で変化します. Eg = 0 V のとき Ep min = 63.8 V , Ip max = 104.5 mA となり, Eg = - 59 V のとき Ep max = 288.8 V , Ip min = 14.5 mA となります.
このときの各部の波形は,図2.4のようになります. また,伝達特性は図2.5のようになります.
ご覧のように,出力(プレート電圧,プレート電流)はかなり歪んだ波形になっています. このとき得られる出力はどれくらいでしょうか?
波形が歪んでいる場合の電力を求める前に, 正弦波について波形(波高値)と電力の関係を調べます. 図2.6の回路で,抵抗に流れる電流 i(t) が
|
i(t) = I sin |
(2.1) |
|
e(t) = i(t)R = IR sin |
(2.2) |
|
p(t) = e(t)i(t) = i2(t)R = I2R sin2 |
(2.3) |
p(t) = I2R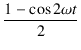
|
(2.4) |
ここで,電力の平均 P
は,p(t)
を1周期分積分したものを周期
2![]() /
/![]() で割ったもの,すなわち,
で割ったもの,すなわち,
P = 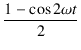 dt dt
|
(2.5) |
|
P = |
(2.6) |
| P = Irms2R | (2.7) |
| Irms2R | = | ||
| Irms | = | (2.8) |
このように,交流を抵抗で消費させたときに,
同じエネルギーを発生する直流の値を実効値と呼びます.
正弦波の場合,波高値の
1/![]() 倍が実効値となります.
倍が実効値となります.
つぎに,基本波の2倍の周波数の歪(第二次高調波)が加わった場合を考えます. 基本波の電流の波高値を I1 ,第二次高調波の電流の波高値を I2 とします. 基本波と高調波を加えた電流の波形 i(t) は,基本波の位相を基準とすると,
|
i(t) = I1sin |
(2.9) |
電力を求めると,
| P | = | R |
|
| = | R |
||
| = | R |
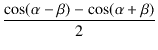
という関係を使うと,
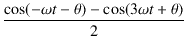 dt dt
|
(2.10) |
という関係を使うと,
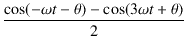 dt dt | |||
| = | (2.11) | ||
|
P = R |
(2.12) |
すなわち,歪みを含んだ波形の電力は, 基本波の成分の電力と,高調波の成分の電力を加えたものになります. ここでは第二次高調波の場合を考えましたが, 基本波の整数倍の高調波であれば,ここまでの式がすべて成り立ちます.
シングル出力段の波形は, 図2.4からわかるように, 基本波の半サイクルで波形が伸び,もう一方の半サイクルでは波形が縮んだものです. このような波形は,二次の高調波によって生じます. したがって,ここでは二次高調波のみが存在する場合を考えます.
基本波の大きさ(波高値)を f
,
第2高調波の大きさを h2
とすると,
2つの波を足し合わせた合成波形は,図2.8のようになります.
ここで,図の縦軸はプレート電流 Ip
とします.
第2高調波の位相は基本波に対して
![]() 90o
となります.
ここで,合成波の始まり(位相0)のプレート電流は,
基本波,第2高調波の中心(平均)
Ipavg
ではなく,
Ipavg - h2
であることに注目してください.
ここが無信号時のプレート電流 Ip0
になります.
90o
となります.
ここで,合成波の始まり(位相0)のプレート電流は,
基本波,第2高調波の中心(平均)
Ipavg
ではなく,
Ipavg - h2
であることに注目してください.
ここが無信号時のプレート電流 Ip0
になります.
図からわかるように,プレート電流の最大値 Ip max は,
であり,プレート電流の最小値 Ip min は, です. 式(2.13)から(2.14)を引くと,| Ip max + Ip min | = | 2Ip0 +4h2 | |
| h2 | = | 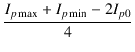 |
(2.16) |
| Ip max | = | Ipavg + f + h2 | (2.17) |
| Ip min | = | Ipavg - f + h2 | (2.18) |
これより,シングル出力段の出力 Po は,
Po = 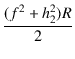
|
(2.21) |
6EM7の例の出力を求めます.
基本波と高調波の波高値は,
| f | = | 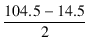 = 45.0 [mA] = 45.0 [mA] |
|
| h2 | = | 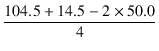 = 4.75 [mA] = 4.75 [mA] |
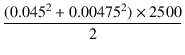 = 2.56 [W]
= 2.56 [W]
となります. 一般に,第二次高調波の比率(歪率)は10%以下ですから, 高調波の電力は基本波の1%以下になるので,第二次高調波の寄与分を無視して, で計算すればよいことになります. この方法で6EM7の出力を計算すると,
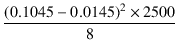 = 2.53 [W]
= 2.53 [W]
となり,さきほどの計算より約1%小さな値となっています.
また,
より,
Po = 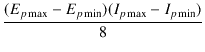
|
(2.23) |
プレート電流の波形から,基本波の波高値 f と, 第二次高調波の波高値 h2 が求められたので,これらより第二次高調波歪率 D2 は,
D2 = 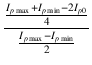 = = 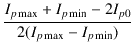 = = 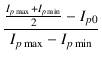
|
(2.24) |
この最後の式の解釈ですが,
まず
![]() について考えます.
Ip max
の時点も Ip min
の時点も第2高調波成分が + となっている時点なので,
平均をとれば,基本波の平均のプレート電流
Ipavg
よりも h2
の分だけ高くなっているはずです.
そこから Ip0
を引けば,h2
の2倍が得られますが,それは高調波のpeak-peak値です.
基本波の方もp-p値すなわち
Ip max - Ip min
を求め,それを分母としてやれば歪率が計算できるということです.
について考えます.
Ip max
の時点も Ip min
の時点も第2高調波成分が + となっている時点なので,
平均をとれば,基本波の平均のプレート電流
Ipavg
よりも h2
の分だけ高くなっているはずです.
そこから Ip0
を引けば,h2
の2倍が得られますが,それは高調波のpeak-peak値です.
基本波の方もp-p値すなわち
Ip max - Ip min
を求め,それを分母としてやれば歪率が計算できるということです.
また,図からわかるように,信号入力時の平均プレート電流 Ipavg は, 無信号時のプレート電流 Ip0 と比べて, 第2高調波の波高値 h2 だけ増加します.
6EM7の例で歪率を計算すると,
となります.
シングル出力段の等価回路はカソード接地と同じですが, 負荷インピーダンスがトランスの公称インピーダンスになります(図2.9).
したがって,出力トランス一次側までの増幅度 A
と,
出力トランス二次側から見た出力インピーダンス Zo
は,
| A | = | - μ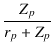 |
(2.25) |
| Zo | = | (2.26) |
ダンピングファクター ![]() は,
は,
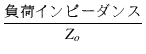
|
(2.27) |
6EM7のゲインと出力インピーダンスは,
動作点の三定数が ![]() = 4.84
,
rp = 826 Ω
,
gm = 5.86 mS
なので,
一次巻線の抵抗を
r1 = 146.8 Ω
,
二次巻線の抵抗を
r2 = 0.66 Ω
,
巻数比を n = 16.7132
とすれば,
= 4.84
,
rp = 826 Ω
,
gm = 5.86 mS
なので,
一次巻線の抵抗を
r1 = 146.8 Ω
,
二次巻線の抵抗を
r2 = 0.66 Ω
,
巻数比を n = 16.7132
とすれば,
| A | = | -4.84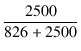 = - 3.64 = - 3.64 |
(2.28) |
| Zo | = | 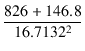 +0.66 = 4.14 [Ω] +0.66 = 4.14 [Ω] |
(2.29) |
ayumi