Subsections

1.2 トランスの等価回路

実際のトランスには，巻線抵抗，一次インダクタンス(励磁インダクタンス)，漏洩インダクタンス，鉄損などがあり，周波数特性やインピーダンス特性に影響してきます．これらの影響を考慮したトランスの等価回路として，図1.3が一般に使われます^1.1．

**図 1.3:** トランスの等価回路(1)
$\begin{figure}\input{figs/tr_eq} \end{figure}$

ここで，

r₁	:	一次巻線抵抗
r₂	:	二次巻線抵抗
C_s1	:	一次巻線浮遊容量
C_s2	:	二次巻線浮遊容量
L_l1	:	一次巻線漏洩インダクタンス
L_l2	:	二次巻線漏洩インダクタンス
L_P	:	一次インダクタンス
R_i	:	鉄損

です．

二次側のインピーダンスは，一次側からみると n² 倍になるので，二次巻線抵抗，二次漏洩インダクタンス，二次巻線浮遊容量をすべて一次側に換算すると，図1.4の等価回路が得られます．

**図 1.4:** トランスの等価回路(2)
$\begin{figure}\input{figs/tr_eq2} \end{figure}$

また，負荷インピーダンス Z_L の両端に生じる電圧が変化しますが， Z_L を一次側から見た値 Z'_L = n²Z_L に換算すれば，理想トランスを取り除くことができ，図1.5の等価回路が得られます．

**図 1.5:** トランスの等価回路(3)
$\begin{figure}\input{figs/tr_eq3} \end{figure}$

1.2.1 中域の等価回路

中域では浮遊容量 C_s は開放とみなせます．一般に漏洩インダクタンス L_l は，一次インダクタンスの 1/1000 以下と微小なので， L_l は短絡とみなせます．一次インダクタンス L_P のインピーダンスは，中域では Z'_L と比べると十分に大きいので，開放とみなせます．

したがって，中域の等価回路は，図1.6の左のようになります．ここで，r'₂ は R_i と比べると十分に小さいので，右のように r₁ と r'₂ をまとめたほうが，解析が容易になり，また影響もほとんどありません．

**図 1.6:** トランスの中域の等価回路
$\begin{figure}\input{figs/tr_eq_m} \end{figure}$

一次に与えられた電力のうち，巻線抵抗 r と鉄損 R_i によって消費される分だけ損失が発生します．これがトランスの定損失といわれるものです．

等価回路より，トランスの一次側の電圧 e₁ と一次側に換算した負荷にかかる電圧 e_2m の関係は，

e₁	=	e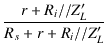 $\displaystyle {\frac{{r + R_i//Z_L'}}{{R_s + r + R_i//Z_L'}}}$	(1.7)
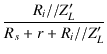e_2m	=	e $\displaystyle {\frac{{R_i//Z'_L}}{{R_s + r + R_i//Z'_L}}}$	(1.8)

となります．したがって，トランスの中域における利得 A_m は，

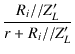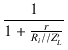A_m	=	$\displaystyle {\frac{{e_{2m}}}{{e_1}}}$ = $\displaystyle {\frac{{R_i//Z'_L}}{{r + R_i//Z'_L}}}$ = $\displaystyle {\frac{{1}}{{1 + \frac{r}{R_i//Z'_L}}}}$
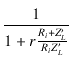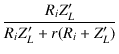	=	$\displaystyle {\frac{{1}}{{1 + r \frac{R_i+Z'_L}{R_i Z'_L}}}}$ = $\displaystyle {\frac{{R_i Z'_L}}{{R_i Z'_L + r(R_i+Z'_L)}}}$
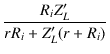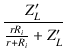	=	$\displaystyle {\frac{{R_i Z'_L}}{{r R_i + Z'_L(r + R_i)}}}$ = $\displaystyle {\frac{{R_i}}{{r+R_i}}}$ ^. $\displaystyle {\frac{{Z'_L}}{{\frac{r R_i}{r+R_i}+Z'_L}}}$
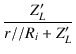	=	$\displaystyle {\frac{{R_i}}{{r+R_i}}}$ ^. $\displaystyle {\frac{{Z'_L}}{{r//R_i+Z'_L}}}$	(1.9)

となります．一般に r $\ll$ R_i ですから，

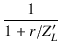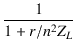
A_m $\displaystyle \approx$ $\displaystyle {\frac{{Z'_L}}{{r+Z'_L}}}$ = $\displaystyle {\frac{{1}}{{1+r/Z_L'}}}$ = $\displaystyle {\frac{{1}}{{1+r/n^2 Z_L}}}$

(1.10)

と近似できます．すなわち，定損失は巻線抵抗によってほぼ決まることがわかります．

電力効率 $\eta$ は，入力電力 p_i に対する出力電力 p_o の比で，この等価回路では，R_i を無視すれば流れる電流は同一ですから，

$\displaystyle \eta$ = $\displaystyle {\frac{{p_o}}{{p_i}}}$ $\displaystyle \approx$ $\displaystyle {\frac{{e_{2m}}}{{e_1}}}$ = $\displaystyle {\frac{{Z'_L}}{{r+Z'_L}}}$

(1.11)

となります．

伝送損失は，r がないと仮定したときの出力電圧 e_2m' に対する出力電圧で定義され，

伝送損失 = 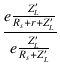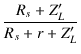$\displaystyle {\frac{{e_{2m}}}{{e_{2m}'}}}$ = $\displaystyle {\frac{{e \frac{Z_L'}{R_s+r+Z_L'}}}{{e \frac{Z_L'}{R_s+Z_L'}}}}$ = $\displaystyle {\frac{{R_s+Z_L'}}{{R_s+r+Z_L'}}}$

(1.12)

一般に， R_s = Z_p $\approx$ Z_L' のときの値が公表されているので，

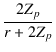
伝送損失 = $\displaystyle {\frac{{2Z_p}}{{r+2Z_p}}}$

(1.13)

となります．

1.2.2 低域の等価回路

低域では一次インダクタンス L_P のインピーダンスが低くなり，無視できなくなります．等価回路は，図1.7のようになります．一次インダクタンスが負荷と並列に入るので，ローカットの特性となります．

**図 1.7:** トランスの低域の等価回路
$\begin{figure}\input{figs/tr_eq_l} \end{figure}$

等価回路より，

e₁	=	e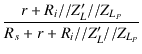 $\displaystyle {\frac{{r+R_i//Z'_L//Z_{L_P}}}{{R_s+r+R_i//Z'_L//Z_{L_P}}}}$	(1.14)
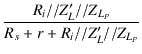e_Ll	=	e $\displaystyle {\frac{{R_i//Z'_L//Z_{L_P}}}{{R_s+r+R_i//Z'_L//Z_{L_P}}}}$	(1.15)

となるので，トランスの低域の利得 A_l は，

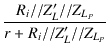
A_l = $\displaystyle {\frac{{e_{2l}}}{{e_1}}}$ = $\displaystyle {\frac{{R_i//Z'_L//Z_{L_P}}}{{r+R_i//Z'_L//Z_{L_P}}}}$

となりますが，中域と同様の式変形を行なうことにより，

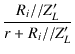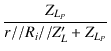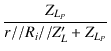A_l	=	$\displaystyle {\frac{{R_i//Z'_L}}{{r + R_i//Z'_L}}}$ ^. $\displaystyle {\frac{{Z_{L_P}}}{{r//R_i//Z'_L+Z_{L_P}}}}$ = A_m $\displaystyle {\frac{{Z_{L_P}}}{{r//R_i//Z'_L+Z_{L_P}}}}$
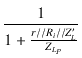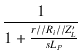	=	A_m $\displaystyle {\frac{{1}}{{1 + \frac{r//R_i//Z'_L}{Z_{L_P}}}}}$ = A_m $\displaystyle {\frac{{1}}{{1 + \frac{r//R_i//Z'_L}{s L_P}}}}$
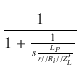	=	A_m $\displaystyle {\frac{{1}}{{1 + \frac{1}{s \frac{L_P}{r//R_i//Z'_L}}}}}$	(1.16)

が得られます．これは，時定数が T_l = L_P/(r//R_i//Z'_L) $\approx$ L_P/r のローカットの特性を表しています．

高域では一次インダクタンスのインピーダンスが高くなり開放とみなせます．周波数が高くなっていくと，まず漏洩インダクタンスの影響が出てきて，次に浮遊容量の影響が出てきます．いずれも高域を減衰させる働きがあります． L_P は開放とみなせるので，L_l をまとめ，さらに C_s をまとめて L_l の右側に置くと，図1.7の等価回路が得られます． C_s の位置は，実際の出力トランスの作動条件では，どちらにあっても大差ないようです．

**図 1.8:** トランスの高域の等価回路
$\begin{figure}\input{figs/tr_eq_h} \end{figure}$

等価回路より，

e₁	=	e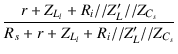 $\displaystyle {\frac{{r+Z_{L_l}+R_i//Z'_L//Z_{C_s}}}{{R_s+r+Z_{L_l}+R_i//Z'_L//Z_{C_s}}}}$	(1.17)
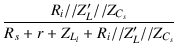e_2h	=	e $\displaystyle {\frac{{R_i//Z'_L//Z_{C_s}}}{{R_s+r+Z_{L_l}+R_i//Z'_L//Z_{C_s}}}}$	(1.18)

ですから，トランスの高域の利得 A_h は，

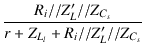A_h	=	$\displaystyle {\frac{{e_{2h}}}{{e_1}}}$ = $\displaystyle {\frac{{R_i//Z'_L//Z_{C_s}}}{{r+Z_{L_l}+R_i//Z'_L//Z_{C_s}}}}$
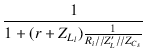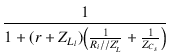	=	$\displaystyle {\frac{{1}}{{1 + (r + Z_{L_l})\frac{1}{R_i//Z_L'//Z_{C_s}}}}}$ = $\displaystyle {\frac{{1}}{{1 + (r + Z_{L_l})\bigl(\frac{1}{R_i//Z_L'}+\frac{1}{Z_{C_s}}\bigr)}}}$
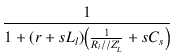	=	$\displaystyle {\frac{{1}}{{1 + (r + s L_l)\bigl(\frac{1}{R_i//Z_L'}+s C_s\bigr)}}}$
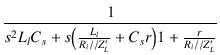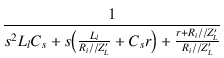	=	$\displaystyle {\frac{{1}}{{s^2 L_l C_s + s\bigl(\frac{L_l}{R_i//Z_L'} + C_s r\bigr) 1 + \frac{r}{R_i//Z_L'}}}}$ = $\displaystyle {\frac{{1}}{{s^2 L_l C_s + s\bigl(\frac{L_l}{R_i//Z_L'} + C_s r\bigr) + \frac{r+R_i//Z_L'}{R_i//Z_L'}}}}$	(1.19)
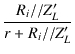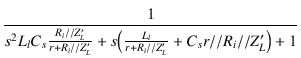	=	$\displaystyle {\frac{{R_i//Z_L'}}{{r+R_i//Z_L'}}}$ ^. $\displaystyle {\frac{{1}}{{s^2 L_l C_s\frac{R_i//Z_L'}{r+R_i//Z_L'} + s\bigl(\frac{L_l}{r+R_i//Z_L'} + C_s r//R_i//Z_L'\bigr) + 1}}}$
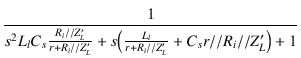	=	A_m $\displaystyle {\frac{{1}}{{s^2 L_l C_s\frac{R_i//Z_L'}{r+R_i//Z_L'} + s\bigl(\frac{L_l}{r+R_i//Z_L'} + C_s r//R_i//Z_L'\bigr) + 1}}}$	(1.20)

となります．これは，二次のローパスの伝達関数で，固有周波数 $\omega_{0}^{}$ と Q は，

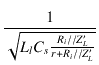$\displaystyle \omega_{0}^{}$	=	$\displaystyle {\frac{{1}}{{\sqrt{L_l C_s\frac{R_i//Z_L'}{r+R_i//Z_L'}}}}}$
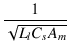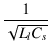	=	$\displaystyle {\frac{{1}}{{\sqrt{L_l C_s A_m}}}}$ $\displaystyle \approx$ $\displaystyle {\frac{{1}}{{\sqrt{L_l C_s}}}}$	(1.21)
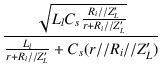Q	=	$\displaystyle {\frac{{\sqrt{L_l C_s \frac{R_i//Z_L'}{r+R_i//Z_L'}}}}{{\frac{L_l}{r+R_i//Z_L'}+C_s(r//R_i//Z_L')}}}$
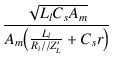	=	$\displaystyle {\frac{{\sqrt{L_l C_s A_m}}}{{A_m\bigl(\frac{L_l}{R_i//Z_L'}+C_s r\bigr)}}}$
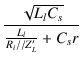	$\displaystyle \approx$	$\displaystyle {\frac{{\sqrt{L_l C_s}}}{{\frac{L_l}{R_i//Z_L'}+C_s r}}}$	(1.22)

となり， Q > 1/ $\sqrt{{2}}$ で周波数特性にピークが生じるようになります．

ayumi
2016-03-07

1.2 トランスの等価回路

1.2.1 中域の等価回路

1.2.2 低域の等価回路

1.2.3 高域の等価回路