Subsections
詳しくは,[6, pp. 187]等を参照してください.
ここでは,管球アンプ用の出力トランスに即して述べていきます.
特に二次巻線の抵抗は 1 Ω
以下なので,
できればブリッジを使って測定すべきですが,
簡易的には中級クラス以上のデジタルマルチメータを使えば,
2桁程度の精度で測定できます.
テストリードの抵抗キャンセル機能が付いている場合は,
それを利用すると簡単に測定できます.
巻線は銅でできており,温度によって抵抗が変わります.
巻線抵抗が大きく影響するのは,定損失と漏洩インダクタンスの測定時です.
定損失のほうは,実際にアンプとして動作させると,巻線の温度が上昇して,
室温で測定した結果よりは損失が大きくなります.
漏洩インダクタンスの測定時には温度上昇はありませんので,
巻線抵抗の測定は室温で行なえばよいと思います.
二次側を開放して一次側に交流信号を加え,二次側の電圧を測定します.
一次側の電圧を e1
, 二次側の電圧を e2
とすれば,巻数比 n
は,
n = 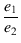
|
(1.23) |
で求められます.
電流がほとんど流れないので,
交流信号の周波数は適当で構わないと思います.
DMMを使う場合は,測定器の精度を考えると 400Hz 程度がよいと思います.
この3つは,二次側を開放して一次側に交流信号を加え,
一次側のインピーダンスの周波数特性を測定して,その結果から算出します.
図1.9のように発振器と抵抗 Rs
をトランスに接続し,
周波数を変えながら,
抵抗の両端の電圧 eR
と,トランスの一次側の電圧 eP
を測定します.
インピーダンス Z
は,
で求めます.
周波数の可変範囲は,50Hz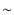 300kHz 程度でよいでしょう.
300kHz 程度でよいでしょう.
図 1.9:
一次インダクタンス,浮遊容量,鉄損の測定回路(左)とその等価回路(右)
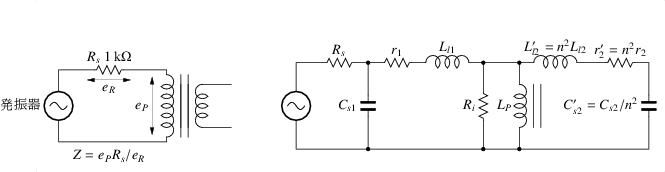 |
等価回路から,
低域では,Cs1
, C's2
は開放,Ll1
, L'l2
は短絡とみなせるため,
インピーダンスは,一次インダクタンスと一次巻線抵抗から構成されます.
したがって,
Z = 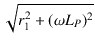
|
(1.25) |
これより,
LP = 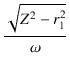 = = 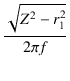
|
(1.26) |
により一次インダクタンスを求めることができます.
ただし,トランスのカタログなどに記載されている一次インダクタンスは,
50Hz,
5 Vrms
で測定されている場合が多く,
また,一次インダクタンスは信号の大きさによりかなり変動するので,
このようにして求めた一次インダクタンスはカタログに記載されている値と
必ずしも一致しないことに注意してください.
周波数を上げていくと,LP
と
Cs = Cs1 + C's2
による並列共振が起こります.
この時のインピーダンスは,
となります.共振周波数は,
f = 1/2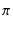
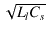 です.
です.
さらに周波数を上げていくと,Cs
のインピーダンスが下がってきて,
Z = 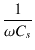
|
(1.28) |
とみなせるようになります.
ここでは,巻線抵抗,漏洩インダクタンス,鉄損を無視しています.
これより,
Cs = 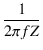
|
(1.29) |
で,総浮遊容量を求めることができます.
さらに周波数を上げていくと,漏洩インダクタンスと C's2
による直列共振が起こり,インピーダンスが急激に下がります.
この時の共振周波数は
f = 1/2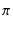
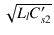 となりますから,
となりますから,
C's2 = 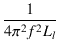
|
(1.30) |
により二次巻線の浮遊容量を求めることができます.
Ll
は,次の節で求めたものを使います.
その直後,Cs1
と C's2
の直列合成容量と漏洩インダクタンスによる並列共振が起こり,インピーダンスが急激に上昇します.
その後は,
-6 dB/oct
でインピーダンスが下がっていきます.
漏洩インダクタンスは,二次側を短絡して一次側に交流信号を加え,
一次側のインピーダンスの周波数特性を測定して,その結果から算出します.
図1.10のように発振器と抵抗をトランスに接続し,
周波数を変えながら,
抵抗の両端の電圧 eR
と,トランスの一次側の電圧 eP
を測定します.
周波数の可変範囲は,10kHz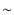 100kHz 程度でよいでしょう.
100kHz 程度でよいでしょう.
図 1.10:
漏洩インダクタンスの測定回路(左)とその等価回路(右)
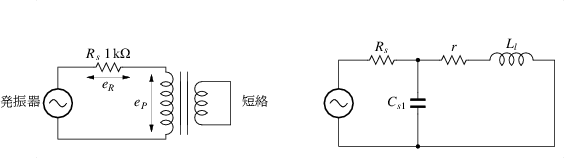 |
等価回路を見るとわかるように,
漏洩インダクタンス Ll
と浮遊容量 Cs1
で並列共振回路を形成しており,
共振周波数でインピーダンスがかなり大きくなります.
共振周波数以下では漏洩インダクタンスが支配的になり,
共振周波数以上では浮遊容量が支配的になり,
インピーダンスのカーブはするどい山を描きます.
共振周波数からある程度離れると,傾きが
6 dB/oct
になります.
インピーダンスカーブの山の左側で,
傾きが
6 dB/oct
になっている適当な周波数のインピーダンスを読み取り,
それを Z
とすれば,
Z = 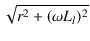
|
(1.31) |
より,
Ll = 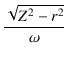 = = 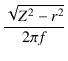
|
(1.32) |
で求めることができます.
周波数をある程度高くとれば(Z
が高いところを読み取る),
r
を無視しても構いませんが,
すぐに共振周波数になってしまうため,r
の補正はおそらく必要となるでしょう.
プッシュプル用の場合,発振器は B
-P1
間につなぎ,
漏洩インダクタンスを測定する際には,
二次を短絡したインピーダンスと,
B
-P2
間を短絡したインピーダンスを別々に測定します.
1.3.5 パラメータの測定例(シングル用)
ここでは,三栄無線KT-88SSMAの出力トランスを測定した例を紹介します.
DMMで測定した結果,一次巻線の抵抗は
r1 = 146.8 Ω
,
二次巻線の抵抗は
r2 = 0.66 Ω
でした.
二次巻線を開放して,400 Hz
の正弦波を加えたところ,
一次側の電圧は
e1 = 1.317 V
,
二次側の電圧は
e2 = 78.8 mV
でした.
これより,巻数比 n
は,
n = 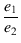 = = 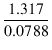 = 16.7132 = 16.7132
|
(1.33) |
となります.
これより,二次巻線抵抗を一次に換算すると,
|
r'2 = n2r2 = 16.71322 x 0.66 = 184.3585 [Ω]
|
(1.34) |
となります.
一次換算の総巻線抵抗 r
は,
|
r = r1 + r'2 = 146.8 + 184.3585 = 331.1585 [Ω]
|
(1.35) |
となります.
電力効率は,
で,-0.6 dB
です.
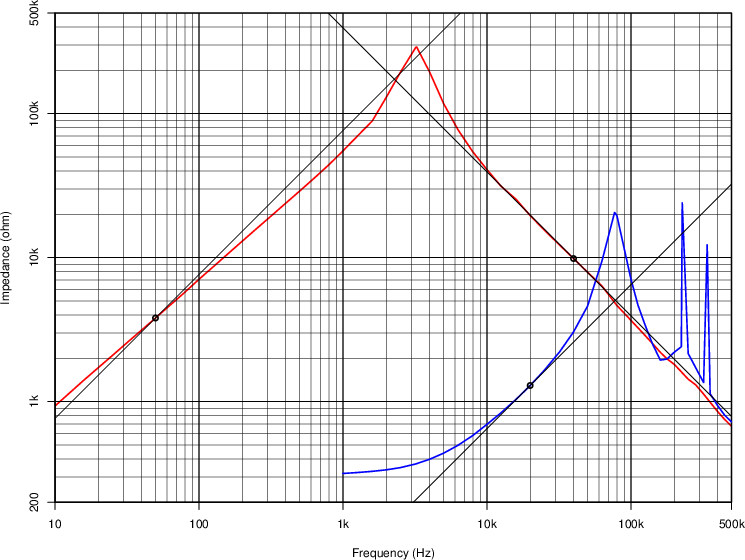
インピーダンスの測定結果を図1.11に示します.
赤い線が二次を開放して測定したインピーダンス,
青い線が二次を短絡して測定したインピーダンスです.
低域の傾きが 6dB になっておらず,
周波数(あるいはレベル)によって一次インダクタンスが変動しています.
二次を開放した 50Hz のインピーダンスは
Zo = 3809 Ω
でした.
これより,一次インダクタンスは,
LP = 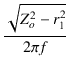 = = 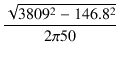 = 12.12 [H] = 12.12 [H]
|
(1.37) |
となります.
図 1.11:
シングル用出力トランスのインピーダンス特性例
|
 |
二次を開放した 40kHz のインピーダンスは
Zo = 9861 Ω
でした.
これより,総浮遊容量は,
Cs = 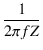 = = 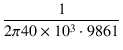 = 403.5 [pF] = 403.5 [pF]
|
(1.38) |
となります.
二次を開放したインピーダンスが最も高くなったのは,
3.25kHz の時で
Zo = 291 kΩ
でした.
巻線抵抗と比べると非常に大きいので,これをそのまま鉄損としてよいでしょう.
二次を短絡した 20kHz のインピーダンスは
Zs = 1295.3 Ω
でした.
これより,漏洩インダクタンスは,
Ll = 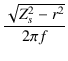 = = 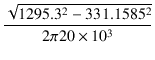 = 9.965 [mH] = 9.965 [mH]
|
(1.39) |
となります.
したがって,結合係数は,次節の式(1.52)より,
K = 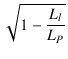 = = 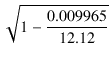 = 0.99959 = 0.99959
|
(1.40) |
となります.
二次を開放したインピーダンスのカーブには,ディップは見られませんでした.
仮に,500kHz のところにディップがあったとすると,
一次側,二次側の浮遊容量は,
| C's2 |
= |
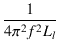 = = 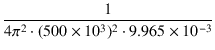 = 10.168 [pF] = 10.168 [pF] |
(1.41) |
| Cs2 |
= |
n2C's2 = 16.71322 . 10.168 x 10-12 = 2840 [pF] |
(1.42) |
| Cs1 |
= |
Cs - C's2 = 403.5 - 10.168 = 393.3 [pF] |
(1.43) |
となります.
1.3.6 パラメータの測定例(プッシュプル用)
ここでは,タムラ製作所F-2021を測定した例を紹介します.
DMMで測定した結果,一次巻線の抵抗は
r11 = 64.7 Ω
,
r12 = 73.5 Ω
,
二次巻線の抵抗は
r2 = 0.25 Ω
でした.
二次巻線を開放して,1kHz の正弦波を加えたところ,
一次側の電圧は
e11 = 3.81 V
,
e12 = 3.80 V
,
二次側の電圧は
e2 = 0.3127 mV
でした.
これより,一次巻線の片側と二次巻線の巻数比 n
は,
n = 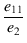 = = 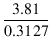 = 12.1842 = 12.1842
|
(1.44) |
となります.
これより,二次巻線抵抗を一次に換算すると,
|
r'2 = n2r2 = 12.18422 x 0.25 = 37.11 [Ω]
|
(1.45) |
となります.
インピーダンスの測定結果を図1.12に示します.
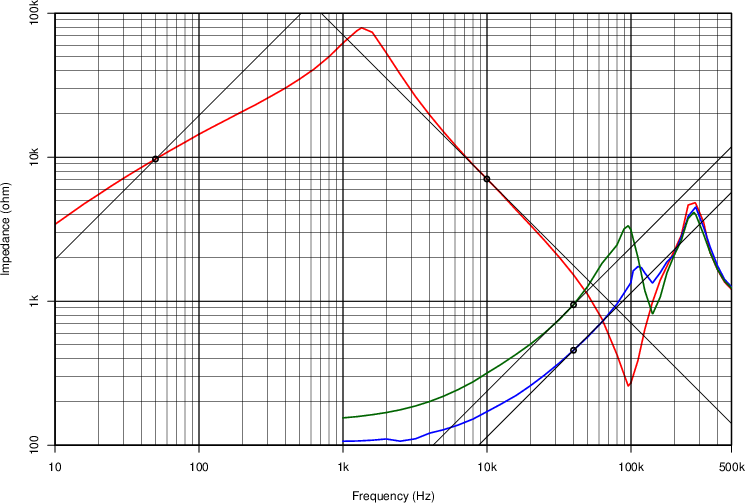
赤い線が二次を開放して測定したインピーダンス,
青い線が二次を短絡して測定したインピーダンス,
緑の線が B
-P2
を短絡して測定したインピーダンスです.
二次を開放した 50Hz のインピーダンスは
Zo = 9715 Ω
でした.
これより,一次インダクタンスは,
LP = 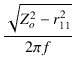 = =  = 30.92 [H] = 30.92 [H]
|
(1.46) |
となります.
図 1.12:
プッシュプル用出力トランスのインピーダンス特性例
|
 |
二次を開放した 10kHz のインピーダンスは
Zo = 7067 Ω
でした.
これより,総浮遊容量は,
Cs = 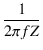 = = 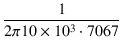 = 2252 [pF] = 2252 [pF]
|
(1.47) |
となります.
この総浮遊容量は,各一次巻線の浮遊容量と,
二次巻線の浮遊容量を一次に換算したものの総和です.
二次を開放したインピーダンスが最も高くなったのは,
1.35kHz の時で
Zo = 79.2 kΩ
でした.
巻線抵抗と比べると非常に大きいので,これをそのまま鉄損としてよいでしょう.
これは,一次の各巻線の鉄損を並列にした値です.
二次を短絡した 40kHz のインピーダンスは
Zs = 456.5 Ω
でした.
これより,一次-二次間の漏洩インダクタンスは,
Llps = 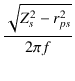 = = 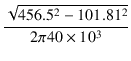 = 1.771 [mH] = 1.771 [mH]
|
(1.48) |
となります.
したがって,結合係数は,次節の式(1.52)より,
Kps = 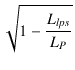 = = 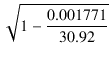 = 0.9999714 = 0.9999714
|
(1.49) |
となります.
B
-P2
間を短絡した 40kHz のインピーダンスは
Zs = 945.2 Ω
でした.
これより,一次巻線間の漏洩インダクタンスは,
Llpp = 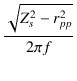 = = 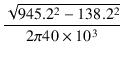 = 3.720 [mH] = 3.720 [mH]
|
(1.50) |
となります.
したがって,結合係数は,
Kpp = 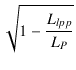 = = 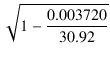 = 0.999940 = 0.999940
|
(1.51) |
となります.
二次を開放したインピーダンスのカーブで,95.8kHz のところに大きなディップがありますが,
これは一次巻線間の漏洩インダクタンスと B
-P2
間の浮遊容量が直列共振しているためで,
二次の浮遊容量によるものではありません.
ayumi
2016-03-07
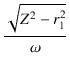 =
= 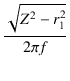
![]()
![]() となりますから,
となりますから,
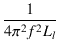
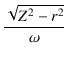 =
= 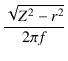
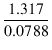 = 16.7132
= 16.7132
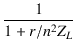 =
= 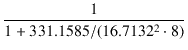 = 0.871
= 0.871
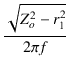 =
= 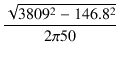 = 12.12 [H]
= 12.12 [H]
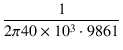 = 403.5 [pF]
= 403.5 [pF]
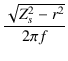 =
= 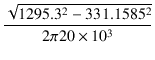 = 9.965 [mH]
= 9.965 [mH]
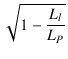 =
= 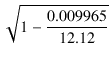 = 0.99959
= 0.99959
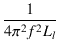 =
= 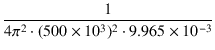 = 10.168 [pF]
= 10.168 [pF]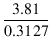 = 12.1842
= 12.1842
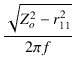 =
=  = 30.92 [H]
= 30.92 [H]
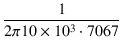 = 2252 [pF]
= 2252 [pF]
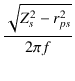 =
= 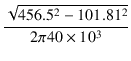 = 1.771 [mH]
= 1.771 [mH]
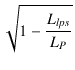 =
= 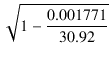 = 0.9999714
= 0.9999714
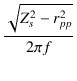 =
= 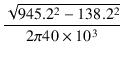 = 3.720 [mH]
= 3.720 [mH]
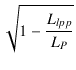 =
= 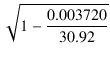 = 0.999940
= 0.999940