Next: 2 ミニアンプの設計 Up: QUAD IIタイプミニアンプ Previous: QUAD IIタイプミニアンプ

1 QUAD IIオリジナル回路

QUAD IIの原回路を図1に示します．

**図 1:** QUAD II原回路
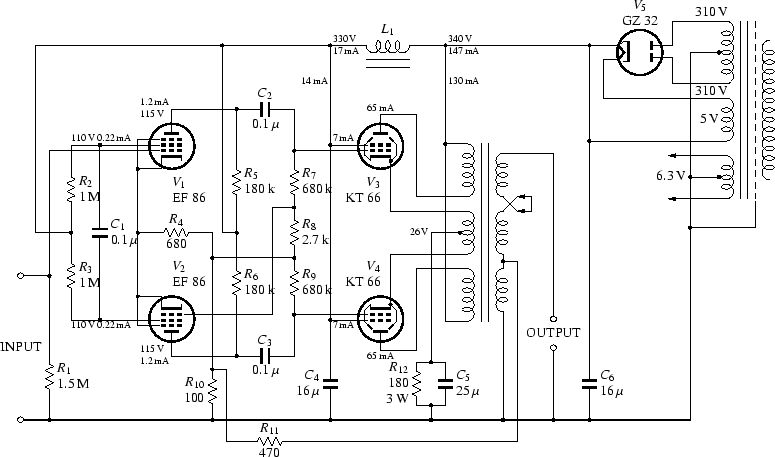
$\begin{figure}\input{quad_sch} \end{figure}$

出力トランスの仕様は詳しくわかりません． [1]によれば，プレートとカソードの巻数比は 9.375 : 1 で，プレート巻線のインピーダンスは 3 kΩ で，カソード巻線により 8 dB の負帰還がかかっているようです．また同書によれば，チョークコイル L₁ は， 30 H となっています．

SPICEによるシミュレーションのリストを以下に示します．

`quad.cir`

    1 Quad II
    2 .INCLUDE 6267.inc
    3 .INCLUDE KT66.inc
    4 .INCLUDE quadopt.inc
    5 
    6 VI 13 0 DC 0 AC 1 SIN(0 2.4 1kHz)
    7 XV1 111 112 13 1 6267
    8 XV2 121 122 23 1 6267
    9 R1 13 0 1.5Meg
   10 R2 91 12 1Meg
   11 R3 91 22 1Meg
   12 C1 12 22 0.1u
   13 R4 1 2 680
   14 R5 11 91 180k
   15 R6 21 91 180k
   16 VIP1 11 111 DC 0
   17 VIG21 12 112 DC 0
   18 VIP2 21 121 DC 0
   19 VIG22 22 122 DC 0
   20 C2 11 31 0.1u
   21 C3 21 41 0.1u
   22 R7 31 23 680k
   23 R8 23 2 2.7k
   24 R9 41 2 680k
   25 R10 2 0 100
   26 R11 2 61 470
   27 *R11 2 0 470
   28 CS 31 41 15p
   29 
   30 XV3 33 32 31 34 KT66
   31 XV4 43 42 41 44 KT66
   32 XOPT 51 90 90 52 44 53 34 61 0 QOPT
   33 VIP3 51 33 0
   34 VIP4 52 43 0
   35 VIG23 91 32 0
   36 VIG24 91 42 0
   37 R12 53 0 180
   38 C5 53 0 25u
   39 
   40 VB2 91 0 330
   41 VB1 90 0 340
   42 
   43 RL 61 0 4
   44 
   45 .NODESET V(11)=130 V(21)=100 V(12)=130 V(22)=93 V(1)=2.0
   46 .NODESET V(53)=26
   47 
   48 .END

`6267.inc`

    1 *
    2 * Generic pentode model: 6267
    3 * Copyright 2003--2008 by Ayumi Nakabayashi, All rights reserved.
    4 * Version 3.10, Generated on Sat Mar  8 22:42:16 2008
    5 *            Plate
    6 *            | Screen Grid
    7 *            | | Control Grid
    8 *            | | | Cathode
    9 *            | | | |
   10 .SUBCKT 6267 A G2 G1 K
   11 BGG   GG   0 V=V(G1,K)+0.59868749
   12 BM1   M1   0 V=(0.010782364*(URAMP(V(G2,K))+1e-10))^-0.70765893
   13 BM2   M2   0 V=(0.67945278*(URAMP(V(GG)+URAMP(V(G2,K))/29.728844)))^2.2076589
   14 BP    P    0 V=0.0013378994*(URAMP(V(GG)+URAMP(V(G2,K))/43.754099))^1.5
   15 BIK   IK   0 V=U(V(GG))*V(P)+(1-U(V(GG)))*0.00078620809*V(M1)*V(M2)
   16 BIG   IG   0 V=0.00066894969*URAMP(V(G1,K))^1.5*(URAMP(V(G1,K))/(URAMP(V(A,K))+URAMP(V(G1,K)))*1.2+0.4)
   17 BIK2  IK2  0 V=V(IK,IG)*(1-0.4*(EXP(-URAMP(V(A,K))/URAMP(V(G2,K))*15)-EXP(-15)))
   18 BIG2T IG2T 0 V=V(IK2)*(0.83966688*(1-URAMP(V(A,K))/(URAMP(V(A,K))+10))^1.5+0.16033312)
   19 BIK3  IK3  0 V=V(IK2)*(URAMP(V(A,K))+7510)/(URAMP(V(G2,K))+7510)
   20 BIK4  IK4  0 V=V(IK3)-URAMP(V(IK3)-(0.00071507731*(URAMP(V(A,K))+URAMP(URAMP(V(G2,K))-URAMP(V(A,K))))^1.5))
   21 BIP   IP   0 V=URAMP(V(IK4,IG2T)-URAMP(V(IK4,IG2T)-(0.00071507731*URAMP(V(A,K))^1.5)))
   22 BIAK  A    K I=V(IP)+1e-10*V(A,K)
   23 BIG2  G2   K I=URAMP(V(IK4,IP))
   24 BIGK  G1   K I=V(IG)
   25 * CAPS
   26 CGA   G1  A  0.05p
   27 CGK   G1  K  2.3p
   28 C12   G1  G2 1.5p
   29 CAK   A   K  5.3p
   30 .ENDS

`KT66.inc`

    1 *
    2 * Generic pentode model: KT66
    3 * Copyright 2003--2008 by Ayumi Nakabayashi, All rights reserved.
    4 * Version 3.10, Generated on Sat Mar  8 22:42:54 2008
    5 *            Plate
    6 *            | Screen Grid
    7 *            | | Control Grid
    8 *            | | | Cathode
    9 *            | | | |
   10 .SUBCKT KT66 A G2 G1 K
   11 BGG   GG   0 V=V(G1,K)+1
   12 BM1   M1   0 V=(0.051887963*(URAMP(V(G2,K))+1e-10))^-0.76669755
   13 BM2   M2   0 V=(0.66175569*(URAMP(V(GG)+URAMP(V(G2,K))/6.5187433)))^2.2666975
   14 BP    P    0 V=0.0018223197*(URAMP(V(GG)+URAMP(V(G2,K))/9.8506796))^1.5
   15 BIK   IK   0 V=U(V(GG))*V(P)+(1-U(V(GG)))*0.0010893248*V(M1)*V(M2)
   16 BIG   IG   0 V=0.00091115984*URAMP(V(G1,K))^1.5*(URAMP(V(G1,K))/(URAMP(V(A,K))+URAMP(V(G1,K)))*1.2+0.4)
   17 BIK2  IK2  0 V=V(IK,IG)*(1-0.4*(EXP(-URAMP(V(A,K))/URAMP(V(G2,K))*15)-EXP(-15)))
   18 BIG2T IG2T 0 V=V(IK2)*(0.938072528*(1-URAMP(V(A,K))/(URAMP(V(A,K))+10))^1.5+0.061927472)
   19 BIK3  IK3  0 V=V(IK2)*(URAMP(V(A,K))+2300)/(URAMP(V(G2,K))+2300)
   20 BIK4  IK4  0 V=V(IK3)-URAMP(V(IK3)-(0.0011955789*(URAMP(V(A,K))+URAMP(URAMP(V(G2,K))-URAMP(V(A,K))))^1.5))
   21 BIP   IP   0 V=URAMP(V(IK4,IG2T)-URAMP(V(IK4,IG2T)-(0.0011955789*URAMP(V(A,K))^1.5)))
   22 BIAK  A    K I=V(IP)+1e-10*V(A,K)
   23 BIG2  G2   K I=URAMP(V(IK4,IP))
   24 BIGK  G1   K I=V(IG)
   25 * CAPS
   26 CGA   G1  A  1.1p
   27 CGK   G1  K  8.1p
   28 C12   G1  G2 5.4p
   29 CAK   A   K  9p
   30 .ENDS

`quadopt.inc`

    1 *
    2 *   QUAD II opt
    3 *
    4 .SUBCKT QOPT P1 B1 B2 P2 S1 S0 S2 X1 X0
    5 * Primary inductance (p-p 3000ohm 11H)
    6 L11 P1 11 2.75H
    7 L12 12 P2 2.75H
    8 * Primary DC resistance
    9 R11 11 B1 100
   10 R12 B2 12 100
   11 * Primary stray capacitance
   12 CP P1 P2 5.52399786225324e-10
   13 * KNF inductance
   14 L13 S1 21 0.03128889H
   15 L14 22 S2 0.03128889H
   16 * KNF DC resistance
   17 R13 S0 21 10.6667
   18 R14 S0 22 10.6667
   19 * Secondary inductance
   20 L15 X1 31 0.01677264H
   21 * Secondary DC resistance
   22 R15 31 X0 0.2694
   23 * coupling factor
   24 K1 L11 L12 0.99989
   25 K2 L11 L13 0.99989
   26 K3 L11 L14 0.99989
   27 K4 L11 L15 0.99989
   28 K5 L12 L13 0.99989
   29 K6 L12 L14 0.99989
   30 K7 L12 L15 0.99989
   31 K8 L13 L14 0.99988
   32 K9 L13 L15 0.99989
   33 K10 L14 L15 0.99989
   34 .ENDS

V₁ の動作点は， E_p0 = 133.3 V, E_g0 = - 2.026 V, E_g20 = 98.55 V, I_p0 = 1.081 mA, I_g20 = 0.2294 mA, g_m = 1.265 mS, r_p = 2611 kΩ, V₂ の動作点は， E_p0 = 128.3 V, E_g0 = - 1.807 V, E_g20 = 91.34 V, I_p0 = 1.109 mA, I_g20 = 0.2366 mA, g_m = 1.314 mS, r_p = 2419 kΩ です． V₁ の特性曲線とロードラインを図2に， V₂ の特性曲線とロードラインを図3に示します．

**図 2:** V₁ の特性曲線とロードライン
$\includegraphics{figs/quad_v1_ll.ps}$

**図 3:** V₂ の特性曲線とロードライン
$\includegraphics{figs/quad_v2_ll.ps}$

1.1.1 古典的負荷分割型

V₁, V₂ のSGにそれぞれパスコンを入れ，カソード-アース間にもパスコンを入れ， R₈ と R₉ の接続点をアースすると，古典的位相反転回路になります(図4)．

この時の動作点は， E_p0 = 132.8 V, E_g0 = - 2.004 V, E_g20 = 97.86 V, I_p0 = 1.084 mA, I_g20 = 0.2301 mA で，三定数は， g_m = 1.269 mS, r_p = 2592 kΩ, μ = 3290, r_g2 = 135.2 kΩ です．これより，ゲイン A は，

A = - g_m(r_p//R_L) = - 1.269 x [2592//180//(680 + 2.7)] = - 171.4 (1)

となります．

R₇ と R₈ によるアッテネータを経由した V₂ への入力は，

-171.4 x 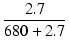$\displaystyle {\frac{{2.7}}{{680 + 2.7}}}$ = - 0.6778 (2)

となって，3.4 dB ほど下側のゲインが足りないことがわかります．

**図 4:** 古典的位相反転
$\begin{figure}\input{quad_ph1} \end{figure}$

シミュレーションでは，上側のゲインが -171.4 (44.7 dB)，下側のゲインが 116.0 (41.3 dB)となって， 3.4 dB の違いが生じています．

周波数特性を図5に示します．低域のカットオフは，この定数の場合，スクリーングリッドのパスコンによって決まります．カットオフ周波数は，

f_c = 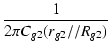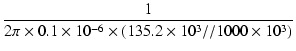$\displaystyle {\frac{{1}}{{2\pi C_{g2}(r_{g2}//R_{g2})}}}$ = $\displaystyle {\frac{{1}}{{2\pi \times 0.1\times 10^{-6} \times (135.2 \times 10^3 // 1000 \times 10^3)}}}$ = 13.36 [Hz]

(3)

となります．下側出力のカットオフは同じく f_c ですが， 2回ローカットを通りますので，f_c における減衰は -6 dB となります．

**図 5:** 古典的位相反転の周波数特性
$\includegraphics{figs/quad_ph1.ps}$

1.1.2 カソード結合

V₁, V₂ のSGにそれぞれパスコンを入れ， V₂ のグリッドをアースに落とすと，カソード結合型の位相反転回路になります(図6)．

**図 6:** カソード結合位相反転
$\begin{figure}\input{quad_ph2} \end{figure}$

それぞれのゲインは，

A₁	=	- $\displaystyle {\frac{{\bigl[1+\frac{r_p+R_L}{(1+\micro)R_k}\bigr]\micro R_L}}{{2(r_p+R_L)+\frac{(r_p+R_L)^2}{(1+\micro)R_k}}}}$	(4)
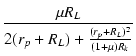A₂	=	$\displaystyle {\frac{{\micro R_L}}{{2(r_p+R_L)+\frac{(r_p+R_L)^2}{(1+\micro)R_k}}}}$	(5)

より， R_L = 142.3 kΩ, R_k = 762.5 Ω を代入して，

A₁	=	- $\displaystyle {\frac{{\bigl[1+\frac{2592+142.3}{(1+3290)\times 0.7625}\bigr]\ti... ... 142.3}}{{2 \times (2592+142.3)+\frac{(2592+142.3)^2}{(1+3290)\times 0.7625}}}}$ = - 115.8	(6)
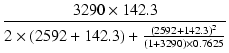A₂	=	$\displaystyle {\frac{{3290 \times 142.3}}{{2\times (2592+142.3)+\frac{(2592+142.3)^2}{(1+3290)\times 0.7625}}}}$ = 55.4	(7)

となり，6.4 dB の差が生じます．

シミュレーションでは，上側のゲインが -115.8 (41.3 dB)，下側のゲインが 55.4 (34.9 dB)となって， 6.4 dB の違いが生じています．

**図 7:** カソード結合位相反転の周波数特性
$\includegraphics{figs/quad_ph2.ps}$

1.1.3 スクリーングリッド結合

カソード-アース間にパスコンを入れ， V₂ のグリッドをアースに落とすと，スクリーングリッド結合型の位相反転回路になります(図8)．

**図 8:** スクリーングリッド結合位相反転
$\begin{figure}\input{quad_ph3} \end{figure}$

シミュレーションでは，上側のゲインが -95.1 (39.6 dB)，下側のゲインが 76.2 (37.6 dB)となって， 1.9 dB の違いが生じています．

スクリーングリッド結合のカットオフ周波数 f_c は，

f_c = 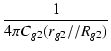$\displaystyle {\frac{{1}}{{4\pi C_{g2}(r_{g2}//R_{g2})}}}$

(8)

ですから，

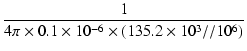f_c = $\displaystyle {\frac{{1}}{{4\pi \times 0.1\times 10^{-6} \times (135.2\times 10^3 // 10^6)}}}$ = 6.68 [Hz]

(9)

となります．

カップリングコンデンサによるカットオフ周波数は，概算で，

f_c = 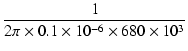$\displaystyle {\frac{{1}}{{2\pi \times 0.1\times 10^{-6} \times 680\times 10^3}}}$ = 2.34 [Hz]

(10)

ですから，カップリングコンデンサのみを大きくしても，カットオフは下がりません．

**図 9:** スクリーングリッド結合位相反転の周波数特性
$\includegraphics{figs/quad_ph3.ps}$

1.1.4 古典的+カソード結合

シミュレーションでは，上側のゲインが -148.5 (43.4 dB)，下側のゲインが 123.4 (41.8 dB)となって， 1.6 dB の違いが生じています．

**図 10:** 古典的+カソード結合位相反転の周波数特性
$\includegraphics{figs/quad_ph4.ps}$

1.1.5 古典的+スクリーングリッド結合

シミュレーションでは，上側のゲインが -136.2 (42.7 dB)，下側のゲインが 127.4 (42.1 dB)となって， 0.58 dB の違いが生じています．

周波数特性では，スクリーングリッド結合のみの場合よりもカットオフ周波数が上昇しています．

**図 11:** 古典的+スクリーングリッド結合位相反転の周波数特性
$\includegraphics{figs/quad_ph5.ps}$

1.1.6 カソード結合+スクリーングリッド結合

シミュレーションでは，上側のゲインが -93.1 (39.4 dB)，下側のゲインが 78.1 (37.9 dB)となって， 1.5 dB の違いが生じています．

**図 12:** カソード結合+スクリーングリッド結合位相反転の周波数特性
$\includegraphics{figs/quad_ph6.ps}$

1.1.7 QUAD IIの位相反転回路

シミュレーションでは，上側のゲインが -138.0 (42.8 dB)，下側のゲインが 129.1 (42.2 dB)となって， 0.58 dB の違いが生じています．

古典的+スクリーングリッド結合よりも少しゲインが上がっていますが，ややバランスが悪くなっています．カソードのパスコンを省いているのは，単に部品点数を減らすためだけかも知れません．

**図 13:** QUAD II位相反転の周波数特性
$\includegraphics{figs/quad_ph7.ps}$

これまでの結果をまとめると，下表のようになります．

形式	上側ゲイン	下側ゲイン	総ゲイン	ゲイン差(dB)
古典的	-171.4	116.0	287.4	3.4
カソード結合	-115.8	55.4	171.2	6.4
G2結合	-95.1	76.2	171.3	1.9
古典的+カソード結合	-148.5	123.4	271.9	1.6
古典的+G2結合	-136.2	127.4	263.6	0.58
カソード結合+G2結合	-93.1	78.1	171.2	1.5
QUAD II	-138.0	129.1	267.1	0.58

古典的な要素が入っている場合は，総ゲインが263.6 $\sim$ 287.4となり，これはその他の場合(171.2)の1.6倍強です．古典的の要素が入っていない場合は，V₂ へのグリッド入力がないので，古典的の V₁ のゲイン(171.4)を2つの出力に分けていることになります． QUAD IIの定数では，V₂ への入力が V₁ への入力の約6割になっています．

負帰還をかける前の各部の周波数特性を図14に示します． OUTPUTは，4 Ω 出力端子のレベルです．

**図 14:** QUAD II無帰還時の周波数特性
$\includegraphics{figs/quad_nonfb.ps}$

カソードにはほとんど信号が発生しないため， ``V1 G-K'' のレベルはほぼ 0 dB です．負帰還を戻すポイント(R₁₀ の上端)では，カソードに生じた信号(``V1, V2 K'')が R₄ と R₁₀ で分圧されるので，非常に小さなレベルになっています(``NF return'')． V2の入力は，V1の約6割なので，``V2 G-K'' は -3 dB 強です．スクリーングリッドには 14 dB ほどの信号が発生しています．出力段の入力は少しアンバランスになっています．高域の特性が揃っていないのは，浮遊容量として V₃, V₄ のグリッド間に 15 pF を付加しているためです．出力端子までのゲインは，40.43倍(32.1dB)です．

1.1.8 負帰還をかけた場合

グローバルの負帰還は，V₁ のカソードに掛かっています．これにより V₂ に対して正帰還がかかるように思えますが， R₈ を通して V₂ のグリッドにもほぼ同じ大きさの信号が与えられるので， V₂ に正帰還は掛かりません．結局 V₂ には，負帰還がかかって減少した V₁ の出力が入力され， V₂ の出力も小さくなります．最終的には，C₁ によりバランスが取れるようになっています．

負帰還をかけた場合の各部の周波数特性を図15に示します．

**図 15:** QUAD II負帰還時の周波数特性
$\includegraphics{figs/quad_nfb.ps}$

出力端子までのゲインは，5.00倍(14.0dB)です．したがって，負帰還量は 32.1 - 14.0 = 18.1 dB となります．無帰還の時にカソードに生じる信号よりも，負帰還の信号の大きさがはるかに大きいので， ``V1, V2 K'' と ``NF return'' のレベルはほとんど同じになっています．正味の V₁ への入力 ``V1 G-K'' は，負帰還のため約1/10となり， -18 dB くらいになっています． V₂ への正味の入力は，ほぼ R₈ の両端に発生した電圧で，これは，V₁ の出力を R₇ と R₈ で分圧したものですから，やはり V₁ への入力の約6割となります．

注目すべきは，G2に生じる信号の大きさで， V₁, V₂ とも 1 kHz 近辺で非常に小さくなっています．つまり，QUAD IIの定数は，中域でG2に信号が発生しないように定められたのではないかと想像できます．また，出力段への入力は良く揃っています．

1.1.9 位相反転段動作の詳細

QUAD IIの位相反転回路を図16に示します．図に付記した信号レベルは，SPICEによるシミュレーションの結果です．

**図 16:** QUAD IIの位相反転回路
$\begin{figure}\input{quadmj_sch} \end{figure}$

前述したように， [1]によれば， QUAD IIの出力トランスのP-P間インピーダンスは 3 kΩ で， P-P巻線とKNF巻線の比は 9.375 : 1 となっています．負帰還を掛けているタップのインピーダンスは不明ですが， 4 Ω 程度のようです．これらの値から，負帰還量は 20 dB 程度となります．

ここで，V₁ と V₂ が完全に対称の動作をしていると仮定しましょう．この場合，プレート電流の信号成分は振幅が同じで，極性は逆です．振幅が大きくない限り，スクリーングリッド電流は，プレート電流にほぼ比例しますから，スクリーングリッド電流の振幅も同じで，極性は逆です．したがってスクリーングリッド電流の信号成分は C₁ を流れるだけですので，スクリーングリッド電圧はグラウンドに対して一定の電圧を保っているはずです．

負帰還は点Aに戻されており，約 20 dB の負帰還が掛かっていると仮定すると，入力に +1 V が加えられたときA点には 0.9 V の電圧が帰還されます． V₁, V₂ の出力が完全にバランスしているとき，カソード結合としての信号は生じず，カソードには，A点とほぼ同じ 0.9 V の電圧が生じます．したがって，V₁ のG-K間入力は 1 - 0.9 = 0.1 V となります．カソードの電圧が変動する一方，スクリーングリッドの対グラウンド電圧は一定ですので，カソードからみたスクリーングリッドの電圧は 0.9 V 下がります．これはコントロールグリッドの電圧が 0.9/μ_g1-g2 V ( μ_g1-g2 はG1-G2間増幅率，不明の場合は三結時の増幅率を使用してもよい)下がったことと等価ですから， V₁ のゲイン A₁ は，

| A₁| = $\displaystyle \Bigl($ 1 - 0.9 - $\displaystyle {\frac{{0.9}}{{\micro_{g1{\rm -}g2}}}}$ $\displaystyle \Bigr)$ g_m(r_p//R_L)

(11)

となります(// は抵抗の並列合成値)．

V₂ のG-K間入力は，R₈ の両端に生じた電圧です．やはり，カソードからみたスクリーングリッドの電圧は 0.9 V 下がりますが，これは，G-K間の信号と同相なので，加え合わせられます．したがって，V₂ のゲイン A₂ は，

A₂ = 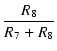$\displaystyle \Bigl($ $\displaystyle {\frac{{R_8}}{{R_7+R_8}}}$ | A₁| + $\displaystyle {\frac{{0.9}}{{\micro_{g1{\rm -}g2}}}}$ $\displaystyle \Bigr)$ g_m(r_p//R_L)

(12)

となります．これら2つのゲインが一致するような R₈ の値を求めれば，位相反転のバランスが取れることになります．

では，一般化して，負帰還量が F の場合を考えます．負帰還量が 20 dB の場合，F = 10 となります．入力が 1 V のとき，カソードに生じる電圧 e_k は，

F = $\displaystyle {\frac{{1}}{{1 - e_k}}}$

(13)

より，

e_k = $\displaystyle {\frac{{F - 1}}{{F}}}$

(14)

となります．上側のゲイン A₁ は，

| A₁| = $\displaystyle \Bigl($ 1 - e_k - $\displaystyle {\frac{{e_k}}{{\micro_{g1{\rm -}g2}}}}$ $\displaystyle \Bigr)$ g_m(r_p//R_L)

(15)

下側のゲイン A₂ は，負荷分割の比率を r = R₈/(R₇ + R₈) とおくと，

A₂ = $\displaystyle \Bigl($ r| A₁| + $\displaystyle {\frac{{e_k}}{{\micro_{g1{\rm -}g2}}}}$ $\displaystyle \Bigr)$ g_m(r_p//R_L)

(16)

2つのゲインが等しくなる条件は，

1 - e_k - $\displaystyle {\frac{{e_k}}{{\micro_{g1{\rm -}g2}}}}$ = r| A₁| + $\displaystyle {\frac{{e_k}}{{\micro_{g1{\rm -}g2}}}}$

より，

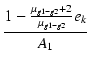r	=	$\displaystyle {\frac{{1 - \frac{\micro_{g1{\rm -}g2}+2}{\micro_{g1{\rm -}g2}}e_k}}{{A_1}}}$
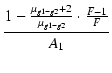	=	$\displaystyle {\frac{{1 - \frac{\micro_{g1{\rm -}g2}+2}{\micro_{g1{\rm -}g2}}\cdot \frac{F-1}{F}}}{{A_1}}}$	(17)

となります．

QUAD IIの例で検証してみましょう． QUAD IIの動作点(V1, V2の平均)の相互コンダクタンスは g_m = 1.3 mS，内部抵抗は r_p = 2500 kΩ， G1-G2間増幅率は μ_g1-g2 = 36.8 で， R_L = 180//680 = 142.3 kΩ ですから，

e_k	=	0.878
\| A₁\|	=	$\displaystyle \Bigl($ 1 - 0.878 - $\displaystyle {\frac{{0.878}}{{36.8}}}$ $\displaystyle \Bigr)$ `x` 1.3 `x` (2500//142.3)
	=	17.2
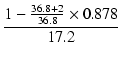r	=	$\displaystyle {\frac{{1 - \frac{36.8+2}{36.8} \times 0.878}}{{17.2}}}$ = 0.00432

となります． R₈ の値は，

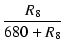$\displaystyle {\frac{{R_8}}{{680 + R_8}}}$ = 0.00432

より，

R₈ = $\displaystyle {\frac{{0.00432}}{{1-0.00432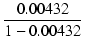}}}$ x 680 = 2.95 [kΩ]

となって，原回路の値( 2.7 kΩ)に非常に近い値となります．実際には，V₂ のほうがバイアスが浅いので，g_m が大きいため， R₈ はこの計算値より低いほうがバランスが取れるでしょう．

もちろん，上下のバランスがくずれた場合は， C₁ の働きによってバランスが保たれますが，中域では古典的負荷分割型の位相反転が過不足なく行なわれていることがわかります．不可解と思われていたQUAD IIの位相反転は，実は負帰還をかけたときに C₁ の働きによらずに上下のバランスを取ったものだったのです．この回路は，R₈ の値を変えてもそれなりの特性を維持するのですが，このように合理的に定められたものであると言えます．

1.1.10 位相反転段の調整

QUAD IIのACバランス調整は，NFBを掛けた状態で行わなければなりません．

歪率計を利用できる場合は，1W程度の出力の歪率を測定し，歪率が最小になるようなR8の値を探します． ACバランスが崩れていることによる偶数次歪みは，出力の大小にかかわらず，一定のレベルで発生しているので，出力段の歪みがそれほど大きくない1W程度では，ACバランスによる歪みが支配的になると思われるからです．

歪率計がない場合は，V1またはV2のスクリーングリッドから， 0.1 $\mu$ F 程度のコンデンサを経由して高入力インピーダンスのAC電圧計に接続し，その読みが最小になるようにR8を調整します． ACバランスを取るのですから，V3, V4のグリッドの電圧が等しくなるように調整しても良いのですが，ここのインピーダンスは高いため，電圧計を接続すると通常の動作と異なってしまう可能性があります．また，よく揃った2台の電圧計が必要となります． 1台の電圧計を使って交互に電圧を測るのでは，V1, V2の負荷の状態が変わってしまうため，うまくありません．

R8の値を変えて，V1, V2のスクリーングリッド，V3, V4のコントロールグリッドに現れる信号電圧の大きさをシミュレートしたのが，図17です．

**図 17:** R8の値に対する，位相反転段のスクリーングリッド，出力段のコントロールグリッドの信号電圧
$\includegraphics{quad_ac.ps}$

厳密に言えば，V3, V4の入力電圧が等しくなるR8の値と，スクリーングリッドの電圧が最小になるR8の値は異なるのですが，スクリーングリッドの電圧が最小になるようにしたときの，出力段の入力のアンバランスは0.1dB程度ですので，十分にバランスしていると言えるでしょう．

1.2 出力段

OPTのP-P間インピーダンスは 3 kΩ で，プレート巻線とカソード帰還巻線の巻数比は 9.375 : 1 ですから，カソード帰還巻線のインピーダンスは，

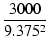$\displaystyle {\frac{{3000}}{{9.375^2}}}$ = 34.13 [Ω]

(18)

となります．プレート-カソード間の負荷インピーダンスは，

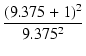3000 x $\displaystyle {\frac{{(9.375 + 1)^2}}{{9.375^2}}}$ = 3674 [Ω] (19)

です．

出力段の動作点は， E_p0 = 309.3 V, E_g0 = - 24.32 V, E_g20 = 305.5 V, I_p0 = 61.76 mA, I_g20 = 4.437 mA, g_m = 5.947 mS, r_p = 37.06 kΩ, μ_g1-g2 = 8.126 です．ロードラインを図18に示します．

**図 18:** KT-66の特性曲線とロードライン
$\includegraphics{figs/quad_p_ll.ps}$

ゲインと出力インピーダンスは，

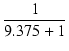$\displaystyle \beta_{{\rm K}}^{}$	=	$\displaystyle {\frac{{1}}{{9.375+1}}}$ = 0.09639	(20)
g_m(UL)	=	5.947 `x` $\displaystyle \bigl($ 1 + 0.09639 `x` $\displaystyle {\frac{{4.437}}{{61.76}}}$ $\displaystyle \bigr)$ = 5.988 [mS]	(21)
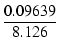$\displaystyle \beta$	=	0.09639 + $\displaystyle {\frac{{0.09639}}{{8.126}}}$ = 0.1083	(22)
A	=	-5.988 `x` (37.06//(3.674/2)) = 10.48	(23)
A_f	=	- 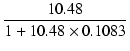$\displaystyle {\frac{{10.48}}{{1 + 10.48 \times 0.1083}}}$ = 4.91	(24)
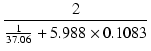Z_o	=	$\displaystyle {\frac{{2}}{{\frac{1}{37.06} + 5.988 \times 0.1083}}}$ = 2.96 [kΩ]	(25)

Next: 2 ミニアンプの設計 Up: QUAD IIタイプミニアンプ Previous: QUAD IIタイプミニアンプ

Ayumi Nakabayashi
平成25年5月19日