Next: 6 おわりに Up: Quad IIタイプミニアンプと位相補償 Previous: 4 スタガ比の決定

5 位相補償の実際

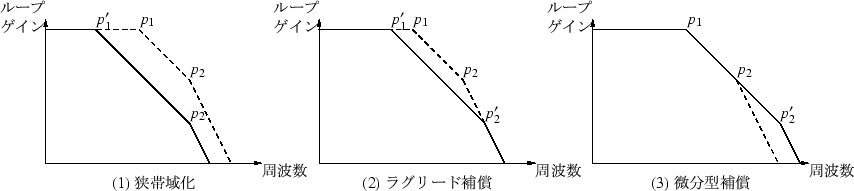
スタガ比を大きくするには，

p₁ を低くする(狭帯域化)
p₁ を低くし，p₂ を高くする(ラグリード補償)
p₂ を高くする(微分型位相補償)

の3通りの方法が考えられます．

**図 6:** 位相補償の方法
$\begin{figure}\input{figs/pcmethod} \end{figure}$

狭帯域化およびラグリード補償は，第一ポール p₁ を生じている箇所で行います．微分型補償は，負帰還回路( $\beta$ 回路)で行うため，一般に p₁ とも p₂ とも干渉せずに定数を決めることができます．狭帯域化と同様な周波数特性を得るために，p₁ 以外の箇所で補償をすることもでき，ステップ補償と呼ばれます．

狭帯域化およびラグリード補償では， p₁ を構成している定数をよく知る必要があります．図7に，QUAD IIタイプの位相反転段と出力段の段間の等価回路を示します．

**図 7:** p₁ の等価回路
$\begin{figure}\input{figs/p1equiv} \end{figure}$

ここで，C_o は位相反転段の出力容量，C_s はミラー効果を含めた出力段の入力容量，また，

r_p	$\displaystyle \approx$	3000 kΩ
R_p	=	150 kΩ
R_g	=	470 kΩ

で，

R₁ = 2r_p//2R_p//2R_g = 219 kΩ

(5)

となります．第一ポールが 20 kHz にあるので，C₁ を求めると，

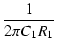
p₁ = $\displaystyle {\frac{{1}}{{2\pi C_1 R_1}}}$

(6)

より，

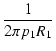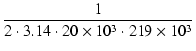C₁ = $\displaystyle {\frac{{1}}{{2\pi p_1 R_1}}}$ = $\displaystyle {\frac{{1}}{{2\cdot 3.14 \cdot 20\times 10^3 \cdot 219\times10^3}}}$ = 36 [pF]

(7)

となります．

5.1 狭帯域化による補償

$\alpha$ = 20 とするためには，移動後の第一ポール p₁' を，

p₁' = 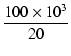$\displaystyle {\frac{{p_2}}{{\alpha}}}$ = $\displaystyle {\frac{{100\times 10^3}}{{20}}}$ = 5 [kHz]

(8)

にする必要があります．これは元の p₁ の 1/4 ですから， C₁ にその3倍のコンデンサを付加して，容量の合計を C₁ の4倍にすれば目的を達することができます．したがって，補償のための容量 C₂ は，

C₂ = (4 - 1)C₁ = 3^.36 = 108 [pF]

(9)

となり，これを出力管のグリッド間(または位相反転段のプレート間)に付け加えます．

インピーダンスが低く，補償容量が大きくなる場合は，出力段のプレート-グリッド間にコンデンサをつければ，ミラー効果により増幅度の分大きなコンデンサの働きをしますから，小さな容量で同等な効果を得ることができます．

5.2 ラグリード補償

第一ポール p₁ がある部分の特性を，図8の左上から右上のように変更できれば，全体の特性を右下のようにすることができ，必要なスタガ比を得ることができます．すなわち，もともとあったポール p₁ を p₁' に移動し， p₂ にゼロを作り，p₂' に新たにポールを作ります．

**図 8:** ラグリード補償
$\begin{figure}\input{figs/laglead} \end{figure}$

このような特性を得るには，図9のように，抵抗とコンデンサを直列にしたものを，第一ポールを生じている部分に入れます．

**図 9:** ラグリード補償の回路
$\begin{figure}\input{figs/lagleadequiv} \end{figure}$

p₁ を p₁' へと低くする比率と， p₂ を p₂' へと高くする比率は等しく，これを $\gamma$ とします．つまり，

$\displaystyle {\frac{{p_1}}{{p_1'}}}$ = $\displaystyle {\frac{{p_2'}}{{p_2}}}$ = $\displaystyle \gamma$

(10)

です．

さて，希望のスタガ比を $\alpha$ とすると，

$\displaystyle \alpha$ = $\displaystyle {\frac{{p_2'}}{{p_1'}}}$ = $\displaystyle {\frac{{\gamma p_2}}{{p_1/\gamma}}}$ = $\displaystyle \gamma^{2}_{}$ $\displaystyle {\frac{{p_2}}{{p_1}}}$

(11)

より，

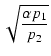
$\displaystyle \gamma$ = $\displaystyle \sqrt{{\frac{\alpha p_1}{p_2}}}$

(12)

となります．この例の場合は，

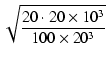$\displaystyle \gamma$ = $\displaystyle \sqrt{{\frac{20 \cdot 20\times10^3}{100\times 20^3}}}$ = 2

(13)

となります．

具体的な定数の求め方ですが，導出方法は理論編でやることにして，ここでは結果だけを書いておきます．ポールの単位は周波数ではなく，角周波数( $\omega$ = 2 $\pi$ f)を使います．

R₂	=	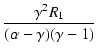$\displaystyle {\frac{{\gamma^2 R_1}}{{(\alpha - \gamma)(\gamma - 1)}}}$	(14)
C₂	=	$\displaystyle {\frac{{1}}{{p_2 R_2}}}$	(15)

この例の場合は，

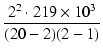R₂	=	$\displaystyle {\frac{{2^2 \cdot 219\times 10^3}}{{(20 - 2)(2 - 1)}}}$ = 48.7 [kΩ]	(16)
C₂	=	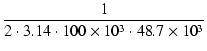$\displaystyle {\frac{{1}}{{2 \cdot 3.14 \cdot 100\times 10^3 \cdot 48.7\times 10^3}}}$ = 32.7 [pF]	(17)

となります．

簡単に定数の目安をつけるには，次のようにします． p₁' は，C₁ と C₂ の並列合成値と R₁ によって概ね決まります．今回の場合，p₁' を p₁ の半分にしたいので， C₂ としては C₁ と同じ値を使えばよいことがわかります．

p₂' は，R₂ と C₂ によって決まります．今回の場合，これが p₂ の2倍となるように，R₂ の値を決めます．

負帰還量 F を変えたときの， R₂, C₂ の値の変化を図10に示します．丸が付いているところは，例として取り上げた $\alpha$ = 20 の場合です(T = 10, F = 11)．

**図 10:** ラグリード補償の帰還量と定数
$\includegraphics{figs/lagleadcr.ps}$

5.3 微分型補償

微分型補償は，図11のように，帰還抵抗 R_f に補償用のコンデンサ C_f を並列に接続し，第二のポール p₂ をさらに高域に移動させるものです．

**図 11:** 微分型補償
$\begin{figure}\input{figs/diff} \end{figure}$

この帰還回路( $\beta$ 回路)には，ゼロ z_f とポール p_f があり，その位置は，

z_f	=	$\displaystyle {\frac{{1}}{{C_f R_f}}}$	(18)
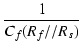p_f	=	$\displaystyle {\frac{{1}}{{C_f (R_f // R_s)}}}$	(19)

となります．帰還回路の中域のゲインは R_s/(R_s + R_f) で， z_f からゲインが上昇し， p_f でゲインが1となり，それ以上の周波数では全帰還となります．単に z_f を p₂ に合わせればよいように思われますが，帰還後の特性を正確に追っていく必要があります．

こちらも，導出は理論編に譲り，結論だけ書きます．

$\displaystyle \omega_{0}^{}$	=	$\displaystyle \sqrt{{(1 + T) p_1 p_2}}$ (負帰還後のカットオフ角周波数)	(20)
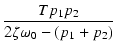z_f	=	$\displaystyle {\frac{{T p_1 p_2}}{{2\zeta \omega_0 - (p_1 + p_2)}}}$ (作成するゼロの角周波数)	(21)
C_f	=	$\displaystyle {\frac{{1}}{{z_f R_f}}}$	(22)

負帰還を 20 dB かけることにすると， F = 10, T = 9 で，バタワース特性にするには $\zeta$ = 0.707 で，ポールの配置は， p₁ = 2 $\pi$ ^.20 x 10³ = 125700, p₂ = 2 $\pi$ ^.100 x 10³ = 628300 ですから， R_f = 470 Ω とすれば，

$\displaystyle \omega_{0}^{}$	=	$\displaystyle \sqrt{{10\cdot 125700 \cdot 628300}}$ = 888700 [rad /s] = 141 [kHz]
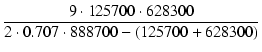z_f	=	$\displaystyle {\frac{{9 \cdot 125700 \cdot 628300}}{{2\cdot 0.707 \cdot 888700 - (125700 + 628300)}}}$ = 1.41 [Mrad /s] = 225 [kHz]
C_f	=	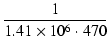$\displaystyle {\frac{{1}}{{1.41\times10^6 \cdot 470}}}$ = 1505 [pF]

となります．

位相補償前のボーデ線図と，位相補償後のボーデ線図を，図12に示します．

**図 12:** 微分型位相補償(左：補償前，右：補償後)
$\includegraphics{figs/diffpc.ps}$

補償前のゲイン交点周波数(ループゲインが1 (0 dB)となる周波数)は， 115.9 kHz で，その時の位相は -129.4^o であり，位相余裕は 180 - 129.4 = 50.6^o となります．このとき，閉ループのゲイン(緑色)の周波数特性にはピークが生じています．

これに微分型の位相補償を行うと，図の右側のようになります． $\beta$ 回路の周波数特性は，図の青線のように z_f から上昇し，最終的にはゲインが1となります． $\beta$ 回路の位相は， 10 kHz あたりから進みはじめ， 600 kHz あたりで進みが最大となり，再び0に戻っていきます．この位相の進みにより，ループ全体の位相の遅れが 100 kHz から 1 MHz あたりで止まり，位相余裕が確保されます．ゲイン交点周波数は， 126.3 kHz で，その時の位相は -107.4^o であり，位相余裕は 180 - 107.4 = 72.6^o となります．閉ループのゲインの周波数特性はフラットになっています．

負帰還量 F を変えたときの， R_f, C_f の値の変化を図13に示します． R_s = 68 Ω としています．

**図 13:** 微分型補償の帰還量と定数
$\includegraphics{figs/diffcr.ps}$

Next: 6 おわりに Up: Quad IIタイプミニアンプと位相補償 Previous: 4 スタガ比の決定

Ayumi Nakabayashi
平成17年6月16日