1 はじめに

Spiceは，非線形直流解析，非線形過渡解析，線形交流解析用の汎用回路シミュレーションプログラムです． 抵抗，コンデンサ，インダクタ，相互インダクタ，独立電圧源，独立電流源，4種類の従属電源，無損失・有損失伝送線路(2つの異なった実装があります)，スイッチ，一様分布RC線，5つのもっとも一般的な半導体素子(ダイオード，バイポーラ接合型トランジスタ(BJT)，JFET, MESFET, MOSFET)によって構成された回路を解析します．

Spice3バージョンは，Spice 2G.6を元にしています． Spice3は，新しい特徴を取り込むように開発されましたが，Spice2プログラムで広く使われている機能やモデルもサポートしています．

Spiceは，半導体素子のモデルを内蔵しており，利用者は必要最小限のモデルのパラメータ値を指定すればよいのです． BJTのモデルは，Gummel and Poonの積分電荷モデルに基づいていますが，Gummel-Poonのパラメータが指定されない場合，モデルはより単純なEbers-Mollモデルになります． どちらの場合でも，電荷蓄積効果，電気抵抗，出力コンダクタンスの電流依存性を反映できます． ダイオードのモデルは，接合型ダイオードおよびショットキーバリアダイオードのどちらにも使えます． JFETモデルは，Shichman and HodgesのFETモデルに基づいています． 6つのMOSFETモデルが実装されています：MOS1はI-V特性の2乗則によって記述され，MOS2 [1] は解析的モデル，MOS3 [1] は半経験的モデル，MOS6 [2] は短チャネル区間で精度の高い単純な解析的モデル，MOS4 [3,4] と MOS5 [5] は，BSIM (Berkeley Short-channel IGFET Model)とBSIM2です． MOS2, MOS3, MOS4 は，チャネル長調整，subthreshold conduction, scattering-limited velocity saturation, small-size effects, charge-controlled capacitancesのような副次的な効果も扱います．

1.1 解析の種類

1.1.1 直流解析

Spiceの直流解析部は，インダクタを短絡し，コンデンサを開放して，回路の直流動作点を決定します． 直流解析のオプションは，制御行 .DC, .TF, .OP で指定します． 直流解析は，過渡解析を行なう場合に過渡現象の初期状態を決定するため，また交流小信号解析を行なう場合に非線形素子の線形化小信号モデルを決定するために，それらの解析に先立って自動的に行なわれます． 必要なら，直流解析の一部として，直流小信号に対する伝達関数の値(入力に対する出力の比)，入力抵抗，出力抵抗も計算できます． 直流解析は，直流伝達特性を描くのにも使えます． つまり，指定された独立電源をユーザが指定した範囲に渡って変化させ，電源の一連の値に対する出力変数の値を保存します．

1.1.2 交流小信号解析

Spiceの交流小信号解析部は，出力変数の周波数特性を計算します． プログラムは，最初に回路の直流動作点を計算し，回路中のすべての非線形素子について線形化した小信号モデルを求めます． 続いて，ユーザが指定した周波数の範囲に渡って，得られた線形回路を解析します． 通常，交流小信号解析の結果は，伝達関数(電圧利得，伝達インピーダンスなど)です． 回路に交流入力が1つしかない場合，出力変数の値がそのまま入力に対する伝達関数となるように，入力の振幅を1とし，位相を0に設定すると便利です．

1.1.3 過渡解析

Spiceの過渡解析部は，出力変数の過渡現象を，ユーザが指定した時間間隔について，時間の関数として計算します． 初期状態は，直流解析によって自動的に決定されます． 時間に依存しないすべての電圧・電流源(たとえば電源)は，それらの DC 値に設定されます． 過渡解析の時間間隔は，制御行 .TRAN で設定します．

1.1.4 極・ゼロ解析

Spiceの極・ゼロ解析部は，小信号交流伝達関数の極とゼロを計算します． プログラムは，最初に直流動作点を計算し，回路のすべての非線形素子について線形化した小信号モデルを求めます． この線形化した回路を使って，伝達関数の極とゼロを見つけます．

2種類の伝達関数を解析できます． 一つは，(出力電圧)/(入力電圧) という形式で，もう一つは，(出力電圧)/(入力電流) という形式です． これらの2種類の伝達関数の形式は，すべてのケースをカバーし，入力/出力インピーダンスや電圧利得などの関数の極/ゼロを見つけることができます． 入力と出力の端子は，ノードのペア2つで指定します．

極・ゼロ解析は，抵抗，コンデンサ，インダクタ，線形従属電源，独立電源，BJT, MOSFET, JFET, ダイオードに対して行なえます． 伝送線路はサポートされていません．

解析には，数値的な局所最適化を用いています． 回路が大きい場合，時間が相当かかったり，すべての極・ゼロを見つけることができない可能性もあります． 回路によっては，この手法は迷子になり，とてつもなく多くの極・ゼロを見つけてしまうことがあります．

1.1.5 小信号歪み解析

Spiceの歪み解析部は，小入力信号に対する定常高調波歪みおよび混変調出力を計算します． 回路の入力として単一周波数の信号が指定された場合，回路中のすべての点について，2次および3次の高調波が複素数で計算されます． 2種類の周波数の入力が回路に加えられた場合， 入力周波数の和と差，および低い周波数と高い周波数の第2高調波との差について，回路変数の複素数値を計算します．

歪み解析は，次の非線形素子に対して行なえます：ダイオード，BJT, JFET, MOSFET (レベル1, 2, 3, 4/BSIM1, 5/BSIM2, 6), MESFET． 歪み解析では，すべての線形素子を使えます． 回路中にスイッチがある場合，歪みの計算のための小さな励振によってスイッチの状態が変わらなければ，解析結果は正しいです．

1.1.6 感応度解析

Spice3は，モデルのパラメータを含むすべての回路変数に関して，出力変数の直流動作点の感応度または交流小信号感応度のいずれかを計算します． Spiceは，各素子の各パラメータを独立に変化させることによって生じる出力変数(ノードの電圧または枝の電流)の差を計算します． この手法は数値的な近似ですから，極端に敏感なパラメータの2次の効果を反映したり，0でない非常に小さな感応度を表わすことができなかったりすることがあります． さらに，各変数は，その値に対する率で変化させられるので，値が0のパラメータは解析されません(これはデータの量が非常に増えるのを防ぐ利益があります)．

1.1.7 ノイズ解析

Spiceのノイズ解析部は，与えられた回路について，素子によって生成されたノイズの解析を行ないます． 入力と出力の端子が指定されると，この解析は，各素子(および素子内の各ノイズ生成源)の出力端子電圧への貢献度を計算します． また，指定された入力に関して，出力ノイズと等価な入力ノイズも計算します． これらの解析は，指定された範囲内のすべての周波数について行なわれます． 計算されたノイズの大きさは，回路変数を定常ガウス確率過程と見なしたスペクトル密度に対応します．

スペクトル密度を計算した後，指定された周波数範囲にわたってこれらの値を積分して(この周波数範囲の)総ノイズ電圧/電流にします． この計算された値は，回路変数を定常ガウス確率過程と見なした分散に対応します．

1.2 異なった温度での解析

Spiceへのすべての入力は，27^o Cで測定されたと仮定されます． この温度は，制御行 .OPTION の TNOM パラメータで変更できます． 温度の影響をモデル化している任意の素子については，モデル自身の TNOM パラメータを指定することによって，温度の値を個別に指定できます． 回路のシミュレーションは，制御行 .OPTION で TEMP パラメータを指定して変更しない限り，27^o Cで実行されます． 個々の素子について，それぞれに TEMP パラメータを指定すれば，回路の温度を変更することができます．

温度依存性は，抵抗，ダイオード，JFET, BJT, レベル1, 2, 3のMOSFETでサポートされています． BSIM MOSFET (レベル4, 5)には，モデルのすべてのパラメータをSpiceに入力する前に調整するという，別の温度依存性のしくみがあります． BSIMの温度調整の詳細については，[6] および [7] を参照してください．

BJTやダイオードのモデル方程式の指数項には，温度が陽に現われています． さらに，飽和電流にも温度依存性が含まれています． BJTの飽和電流の温度依存性は，次の式によって決定されます．

I_S(T₁) = I_S(T₀)$$\biggl($$$${\frac{{T_1}}{{T_0}}}$$$$\biggr)^{{\it XTI}}_{}$$exp$$\biggl($$$${\frac{{E_g q(T_1 T_0)}}{{k(T_1 - T_0)}}}$$$$\biggr)$$

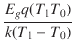
ここで，k はボルツマン定数，q は電荷，E_g はエネルギーギャップ(モデルのパラメータ)，$\it XTI$ は飽和電流温度指数(モデルのパラメータで，通常は3)です．

順方向および逆方向のベータの温度依存性は，次の式によります．

B(T₁) = B(T₀)$$\biggl($$$${\frac{{T_1}}{{T_0}}}$$$$\biggr)^{{\it XTB}}_{}$$

ここで，T₁ および T₀ は絶対温度，$\it XTB$ はユーザが指定するモデルのパラメータです． ベータに対する温度の影響は，B_F , I_{$\it SE$} , B_R , I_{$\it SC$} の値(それぞれSpiceのモデルパラメータ BF, ISE, BR, ISC)を適切に調整することによって反映されます．

接合型ダイオードモデルの飽和電流の温度依存性は，次の式によって決定されます．

I_S(T₁) = I_S(T₀)$$\biggl($$$${\frac{{T_1}}{{T_0}}}$$$$\biggr)^{{\frac{\it XTI}{N}}}_{}$$exp$$\biggl($$$${\frac{{E_g q(T_1 T_0)}}{{N k(T_1 - T_0)}}}$$$$\biggr)$$

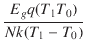
ここで，N はエミッション定数(モデルのパラメータ)，その他の記号の意味は上記と同じです． ショットキーバリアダイオードの飽和電流の温度指数 XTI は，通常2です．

すべての素子モデルについて，温度は接合電位の値 U (Spiceでは PHI)に陽に現われます． 温度依存性は，次の式によって決定されます．

U(T) = $${\frac{{kT}}{{q}}}$$log_e$$\biggl($$$${\frac{{N_a N_d}}{{N_i(T)^2}}}$$$$\biggr)$$

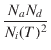
ここで，k はボルツマン定数，q は電荷，N_a はアクセプタ不純物濃度，N_d はドナー不純物濃度，N_i は固有キャリア濃度，E_g はエネルギーギャップです．

MOSFETモデルでは，表面移動性の値 M₀ (すなわち UO)に温度が陽に現われます． 温度依存性は，次の式で決定されます．

M₀(T) = $${\frac{{M_0(T_0)}}{{\Bigl(\displaystyle\frac{T}{T_0}\Bigr)^{1.5}}}}$$

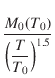
抵抗の温度による影響は，次の式でモデル化されています．

R(T) = R(T₀)[1 + $$\it TC_{1}^{}$$(T - T₀) + $$\it TC_{2}^{}$$(T - T₀)²]

ここで，T は回路の温度，T₀ は名目温度， $\it TC_{1}^{}$ , $\it TC_{2}^{}$ は1次および2次の温度係数です．

1.3 収束

直流動作点および過渡解析の解は，繰り返し計算によって求めます． 以下の2つの条件が両方成立した時に，繰り返し計算が終了します．

1. 非線形の枝の電流が許容値(0.1%または1pA ( 1 x 10^-12 A)のいずれか大きな方)内に収束した．
2. ノードの電圧が許容値(0.1%または1$\mu$ V ( 1 x 10^-6 V)のいずれか大きな方)内に収束した．

Spiceで使われているアルゴリズムは，とても信頼できるものですが，解に収束するとは限りません． このような場合，プログラムはそのジョブを中止します．

直流解析が収束しない場合，主に回路のつなぎ方，要素の値，モデルのパラメータ値の指定に誤りがあります． 循環的な(再生式の)スイッチング回路すなわち正帰還のある回路は，帰還回路内のいくつかの素子に OFF オプションを使うか，または回路が希望の状態に収束するようにするための制御行 .NODESET オプションを使うかしない限り，直流解析ではおそらく収束しないでしょう．