3 回路の要素とモデル

不等号(`$\langle$ ' `$\rangle$ ')で囲まれているデータフィールドは，オプションです． 明示されている区切り文字(括弧，等号など)は，オプションですが，区切り文字の存在を表わしています． 将来の実装では，その区切り文字を必要とすることもあるでしょう． ここで示した区切り文字の付け方に一貫して従っていれば，入力ファイルが読みやすくなるでしょう． Spiceは，枝の電圧および電流に関して(電流は電圧が下がる方向に流れるといった)一貫した表わし方を用います．

3.1 基本的な素子

3.1.1 抵抗

一般形:

RXXXXXXX N1 N2 VALUE

例:

R1 1 2 100
RC1 12 17 1K

N1 と N2 は，要素のノードです． VALUE は抵抗値($\Omega$ )で，正でも負でもかまいませんが，0ではいけません．

3.1.2 半導体抵抗

一般形:

RXXXXXXX N1 N2 $\langle$ VALUE$\rangle$ $\langle$ MNAME$\rangle$ $\langle$ L=LENGTH$\rangle$ $\langle$ W=WIDTH$\rangle$ $\langle$ TEMP=T$\rangle$

例:

RLOAD 2 10 10K
RMOD 3 7 RMODEL L=10u W=1u

これは第3.1.1節で示されている抵抗をさらに一般的にしたもので，温度の影響をモデル化しており，幾何的な情報とプロセスの仕様から実際の抵抗値を計算します． VALUE が指定されていれば，幾何的な情報に優先して抵抗値が定義されます． MNAME が指定されていれば，モデル MNAME の中のプロセスの情報と，与えられた LENGTH と WIDTH から抵抗値が計算されます． VALUE が指定されていない場合，MNAME と LENGTH を指定しなければなりません． WIDTH が指定されていない場合，モデルで与えられているデフォルトの幅が使われます． (オプションの) TEMP は，素子が動作する温度で .OPTION 制御行の温度設定よりも優先します．

3.1.3 半導体抵抗モデル(R)

この抵抗モデルは，幾何的な情報から抵抗値を計算し，温度の修正を行なえるような，プロセスに関連した素子のデータによって構成されます． 使用できるパラメータは以下のとおりです．

名前	パラメータ	単位	省略値	例
TC1	1次の温度係数	Z/o C	0.0	--
TC2	2次の温度係数	Z/o C2	0.0	--
RSH	シート抵抗	Z/[]	--	50
DEFW	省略時の幅	m	1e-6	2e-6
NARROW	エッチングによる側面の狭まり	m	0.0	1e-7
TNOM	パラメータ測定時の温度	o C	27	50

シート抵抗は狭まりのパラメータおよび抵抗素子の L と W と共に使われ，次の式により名目抵抗が決まります．

R = $$\it RSH$$$${\frac{{L - {\it NARROW}}}{{W - {\it NARROW}}}}$$

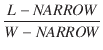
DEFW は，素子の W が指定されていない場合の省略時の値として使われます． RSH または L のいずれかが指定されていない場合，標準の省略時の抵抗値 1kZが使われます． TNOM は，.OPTIONS 制御行で与えられる回路全体の値を上書きするために使われ，このモデルのパラメータが別な温度で測定されたことを表わします． 名目抵抗が計算された後，次の式により温度の影響を反映します．

R(T) = R(T₀)[1 + $$\it TC_{1}^{}$$(T - T₀) + $$\it TC_{2}^{}$$(T - T₀)²]

3.1.4 コンデンサ

一般形:

CXXXXXXX N+ N- VALUE $\langle$ IC=INCOND$\rangle$

例:

CBYP 13 0 1UF
COSC 17 23 10U IC=3V

N+ と N- は，それぞれ正と負のノードです． VALUE はファラド単位の静電容量です．

(オプションの)初期状態は，当初(時刻0)のコンデンサの電圧(単位 V)です． 初期状態がもし指定されていても，.TRAN 制御行に UIC オプションが指定されている場合「のみ」適用されます．

3.1.5 半導体コンデンサ

一般形:

CXXXXXXX N1 N2 $\langle$ VALUE$\rangle$ $\langle$ MNAME$\rangle$ $\langle$ L=LENGTH$\rangle$ $\langle$ W=WIDTH$\rangle$ $\langle$ IC=VAL$\rangle$

例:

CLOAD 2 10 10P
CMOD 3 7 CMODEL L=10u W=1u

これは第3.1.4節で説明したコンデンサの，より一般的な形式で，実際のコンデンサの容量を，厳密に幾何的な情報およびプロセスの仕様から計算できます． VALUE が指定された場合，それにより静電容量が定義されます． MNAME が指定された場合，モデル MNAME のプロセスの情報と，指定された LENGTH と WIDTH から静電容量が計算されます． VALUE が指定されていない場合，MNAME および LENGTH を指定しなければなりません． WIDTH が指定されていない場合，モデルの省略時の幅が使われます． VALUE または MNAME, LENGTH, WIDTH のどちらかを指定しますが，両方指定してはなりません．

3.1.6 半導体コンデンサモデル(C)

コンデンサモデルは，厳密に幾何的な情報から静電容量を計算するのに使われる情報からなります．

名前	パラメータ	単位	省略時の値	例
CJ	ジャンクション底部容量	F/m2	--	5e-5
CJSW	ジャンクション側壁容量	F/m	--	2e-11
DEFW	省略時素子幅	m	1e-6	2e-6
NARROW	側面のエッチングによる狭まり	m	0.0	1e-7

コンデンサの容量は次の式で計算されます．

$$\it CAP$$ = C_J($$\it LENGTH$$ - $$\it NARROW\/$$)($$\it WIDTH$$ - $$\it NARROW\/$$) + 2C_{$\it JSW$}($$\it LENGTH$$ + $$\it WIDTH$$ -2$$\it NARROW$$)

3.1.7 インダクタ

一般形:

LYYYYYYY N+ N- VALUE $\langle$ IC=INCOND$\rangle$

例:

LLINK 42 69 1UH
LSHUNT 23 51 10U IC=15.7MA

N+ と N- は，それぞれ正と負のノードです． VALUE はヘンリー単位のインダクタンスです．

(オプションの)初期条件は，当初(時刻0)に N+ からインダクタを通って N- へ流れる電流(単位 A)の大きさです． 初期状態がもし指定されていても，.TRAN 制御行に UIC オプションが指定されている場合「のみ」適用されます．

3.1.8 相互インダクタ

一般形:

KXXXXXXX LYYYYYYY LZZZZZZZ VALUE

例:

K43 LAA LBB 0.999
KXFRMR L1 L2 0.87

LYYYYYYY と LZZZZZZZ は2つの結合されたインダクタの名前で，VALUE は結合係数 K です． 結合係数は0を超え1以下の値です． 「ドット」の規約に従い，各インダクタの最初のノードにドットが付きます．

3.1.9 スイッチ

一般形:

SXXXXXXX N+ N- NC+ NC- MODEL $\langle$ ON$\rangle$ $\langle$ OFF$\rangle$
WYYYYYYY N+ N- VNAM MODEL $\langle$ ON$\rangle$ $\langle$ OFF$\rangle$

例:

s1 1 2 3 4 switch1 ON
s2 5 6 3 0 sm2 off
Switch1 1 2 10 0 smodel1
w1 1 2 vclock switchmod1
W2 3 0 vramp sm1 ON
wreset 5 6 vclck lossyswitch OFF

ノード1および2は，スイッチの端子がつながるノードです． モデル名は必須で，初期条件はオプションです． 電圧制御スイッチでは，ノード3と4は，それぞれ正および負の制御ノードです． 電流制御スイッチでは，制御電流は指定された電圧源を流れる電流です． 制御電流の正の方向は，正のノードから電圧源を通り負のノードへと流れる方向です．

3.1.10 スイッチモデル(SW/CSW)

スイッチモデルは，Spiceで使えるほとんど理想的なスイッチです． このスイッチは，抵抗が0から無限大へと変化するのではなく，常に有限の正の値をとるという意味で，まったく理想的であるとは言えません． 開閉時の抵抗値を適切に選択することにより，他の回路の要素と比較して実質的に0と無限大にみなせます． 使えるパラメータは以下のとおりです．

名前	パラメータ	単位	省略時の値	スイッチ
VT	threshold電圧	V	0.0	S
IT	threshold電流	A	0.0	W
VH	ヒステリシス電圧	V	0.0	S
IH	ヒステリシス電流	A	0.0	W
RON	閉抵抗	Z	1.0	両方
ROFF	開抵抗	Z	1/GMIN*	両方

*(GMIN の説明については4.1節の .OPTIONS 制御行を参照のこと． 省略時の開抵抗の値は 10¹² $\Omega$ になります．)

スイッチのような高度に非線形な理想的な要素を使うと，回路のノードの電圧に大きな不連続性が生じる場合があります． スイッチの状態が変化することによって引き起こされる急速な変化は，数値の丸め誤差や許容誤差の問題を起こし，間違った結果や時間ステップ(による解析)が困難な状況へとつながります． スイッチを使う場合，以下のステップを踏むことにより，この状況を改善できます．

まず，理想的なスイッチのインピーダンスを回路の他の要素と比べて無視できるくらいにわずかに高くあるいは低く設定するのが懸命です． すべての場合において「理想的」に近いインピーダンスをスイッチに設定すると，上述した非連続性の問題を悪化させます． もちろん，MOSFETのような実際の素子をモデル化する場合，モデル化する素子の大きさに応じた現実的なレベルにオン抵抗を調整すべきです．

スイッチに広範囲のオン/オフ抵抗( ROFF/RON > 10¹² )を設定しなければならない場合，.OPTIONS 制御行を使って TRTOL を省略時の値7.0以下に設定して，過渡解析時の許容誤差を下げるべきです． コンデンサのまわりにスイッチを置いたとき，オプション CHGTOL も下げるべきです． これらの2つのオプションの推奨値は，それぞれ1.0と 1e-16 です． こららの変更により，回路の急速な変化による誤りが起きないよう，Spice3がスイッチの接点をより注意深く扱うように指示します．

3.2 電圧源，電流源

3.2.1 独立電圧源，電流源

一般形:

VXXXXXXX N+ N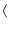- $\langle$ $\langle$ DC$\rangle$ DC/TRAN_VALUE$\rangle$ $\langle$ AC $\langle$ ACMAG $\langle$ ACPHASE$\rangle$ $\rangle$ $\rangle$
+ $\langle$ DISTOF1 $\langle$ F1MAG $\langle$ F1PHASE$\rangle$ $\rangle$ $\rangle$ $\langle$ DISTOF2 $\langle$ F2MAG $\langle$ F2PHASE$\rangle$ $\rangle$ $\rangle$
IYYYYYYY N+ N-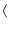 $\langle$ $\langle$ DC$\rangle$ DC/TRAN_VALUE$\rangle$ $\langle$ AC $\langle$ ACMAG $\langle$ ACPHASE$\rangle$ $\rangle$ $\rangle$
+ $\langle$ DISTOF1 $\langle$ F1MAG $\langle$ F1PHASE$\rangle$ $\rangle$ $\rangle$ $\langle$ DISTOF2 $\langle$ F2MAG $\langle$ F2PHASE$\rangle$ $\rangle$ $\rangle$

例:

VCC 10 0 DC 6
VIN 13 2 0.001 AC 1 SIN(0 1 1MEG)
ISRC 23 21 AC 0.333 45.0 SFFM(0 1 10K 5 1K)
VMEAS 12 9
VCARRIER 1 0 DISTOF1 0.1 -90.0
VMODULATOR 2 0 DISTOF2 0.01
IIN1 1 5 AC 1 DISTOF1 DISTOF2 0.001

N+ と N- は，それぞれ正および負のノードです． 電圧源は，必ずしも接地する必要はありません． 正の電流の向きは，正のノードから電圧源を通り負の端子へ流れる方向です． 正の値の電流源では，N+ ノードから，電流源を通り N- 端子へと電流が流れます． 電圧源は，回路を動作させるために使われるだけでなく，Spiceの「電流計」としても使われます． すなわち，電流を測定するには値を0にした電圧源を回路に挿入します． そのようにしても，電圧源は回路をショートしていると見なされるため，回路の動作にまったく影響しません．

DC/TRAN_VALUE は，直流解析および過渡解析の場合の電源の値です． 直流解析，過渡解析用の値が0の場合，この値を省略することができます． 電圧源，電流源の値が時刻により変化しない(電源など)場合，値の前に DC を付けても構いません．

ACMAG は交流の振幅，ACPHASE は交流の位相です． 電源は交流解析時にこの値に設定されます． キーワード AC の後ろで ACMAG が省略された場合，1が仮定されます． ACPHASE が省略された場合，0が仮定されます． この電源が交流小信号の入力でない場合は，キーワード AC と交流の値を省略します．

DISTOF1 と DISTOF2 は，独立電源にそれぞれ周波数が F1 および F2 の歪みの入力があることを指定するキーワードです(4.3.3節の .DISTO 制御行の説明を参照のこと)． キーワードに続けて，オプションで振幅と位相を指定します． 振幅と位相の省略時の値は，それぞれ1.0と0.0です．

過渡解析用に，時刻に依存する値を電源に指定することができます． 時刻に依存する値を指定した場合，直流解析では時刻0の値が使われます． パルス，指数，正弦波，折れ線，単一周波数のFMといった，時刻に依存した関数が5つあります． 電圧源，電流源の値(振幅)以外のパラメータが省略された，または0に設定された場合，示された省略時の値が仮定されます． (TSTEP は表示用の増分であり，TSTOP は最終の時刻です(説明は3.3節の .TRAN 制御行を参照のこと)．)

3.2.1.1 パルス

一般形:

PULSE(V1 V2 TD TR TF PW PER)

例:

VIN 3 0 PULSE(-1 1 2NS 2NS 2NS 50NS 100NS)

パラメータ	省略時の値	単位
V1 (初期値)		V または A
V2 (パルス時の振幅)		V または A
TD (遅延時間)	0.0	秒
TR (立ち上がり時間)	TSTEP	秒
TF (立ち下がり時間)	TSTEP	秒
PW (パルスの幅)	TSTOP	秒
PER (周期)	TSTOP	秒

パルスの波形は次のようになります．

時刻	値
0	V1
$\tt\it {TD}$	V1
$\tt\it {TD}$ + $\tt\it {TR}$	V2
$\tt\it {TD}$ + $\tt\it {TR}$ + $\tt\it {PW}$	V2
$\tt\it {TD}$ + $\tt\it {TR}$ + $\tt\it {PW}$ + $\tt\it {TF}$	V1
TSTOP	V1

中間の値は，線形補間によって決まります．

3.2.1.2 正弦波

一般形:

SIN(VO VA FREQ TD THETA)

例:

VIN 3 0 SIN(0 1 100MEG 1NS 1E10)

パラメータ	省略時の値	単位
VO (オフセット)		V または A
VA (振幅)		V または A
FREQ (周波数)	1/TSTOP	Hz
TD (遅延)	0.0	秒
THETA (減衰係数)	0.0	1/秒

波形は次のようになります．

時刻	値
0から TD	VO
TD から TSTOP	VO + VAe(t-$\it TD$)$\it THETA$sin(2$\pi$$\it FREQ$(t + $\it TD$))

3.2.1.3 指数

一般形:

EXP(V1 V2 TD1 TAU1 TD2 TAU2)

例:

VIN 3 0 EXP(-4 -1 2NS 30NS 60NS 40NS)

パラメータ	省略時の値	単位
V1 (初期値)		V または A
V2 (パルス時の値)		V または A
TD1 (立ち上がり遅延時間)	0.0	秒
TAU1 (立ち上がり時定数)	TSTEP	秒
TD2 (立ち下がり遅延時間)	$\tt\it {TD1}$ + TSTEP	秒
TAU2 (立ち下がり時定数)	TSTEP	秒

波形は次のようになります．

時刻	値
0 から TD1	V1
TD1 から TD2	V1 + (V2 - V1)$\bigl($1 - e${\frac{{-(t - {\it TD}_1)}}{{{\it TAU}_1}}}$$\bigr)$
TD2 から TSTOP	V1 + (V2 - V1)$\bigl($1 - e${\frac{{-(t - {\it TD}_1)}}{{{\it TAU}_1}}}$$\bigr)$ + (V1 - V2)$\bigl($1 - e${\frac{{-(t - {\it TD}_2)}}{{{\it TAU}_2}}}$$\bigr)$

3.2.1.4 折れ線

一般形:

PWL(T1 V1 $\langle$ T2 V2 T3 V3 T4 V4 ...$\rangle$ )

例:

VCLOCK 7 5 PWL(0 -7 10NS -7 11NS -3 17NS -3 18NS -7 50NS -7)

値の組 (Ti, Vi) は， 時刻 = $\tt\it {Ti}$ における電源の値を Vi (VまたはA)と指定します． 中間の時刻における値は，入力された値を線形補間したものになります．

3.2.1.5 単一周波数FM

一般形:

SFFM(VO VA FC MDI FS)

例:

V1 12 0 SFFM(0 1M 20K 5 1K)

パラメータ	省略時の値	単位
VO (オフセット)		V または A
VA (振幅)		V または A
FC (搬送波周波数)	1/TSTOP	Hz
MDI (変調指数)
FS (信号周波数)	1/TSTOP	Hz

波形は次の式になります．

V(t) = V_O + V_Asin$$\bigl($$2$$\pi$$F_Ct + $$\it MDI$$sin(2$$\pi$$F_St)$$\bigr)$$

3.2.2 線形依存電圧源，電流源

Spiceでは，次の4つの式で表わされる線形依存電圧源，電流源を使えます．

i = gv        v = ev        i = fi        v = hi

ここで，g , e , f , h は，それぞれ相互コンダクタンス，電圧増幅度，電流増幅度，相互抵抗を表わす定数です．

3.2.2.1 電圧制御線形電流源

一般形:

GXXXXXXX N+ N- NC+ NC- VALUE

例:

G1 2 0 5 0 0.1MMHO

N+ および N- は，それぞれ正と負のノードです． 電流は，正のノードから電圧源を通って，負のノードへと流れます． NC+ および NC- は，それぞれ正と負の制御ノードです． VALUE は相互コンダクタンス(単位 $\mho$ ，今は S)です．

3.2.2.2 電圧制御線形電圧源

一般形:

EXXXXXXX N+ N- NC+ NC- VALUE

例:

E1 2 3 14 1 2.0

N+ および N- は，それぞれ正と負のノードです． NC+ および NC- は，それぞれ正と負の制御ノードです． VALUE は電圧増幅率です．

3.2.2.3 電流制御線形電流源

一般形:

FXXXXXXX N+ N- VNAM VALUE

例:

F1 13 5 VSENS 5

N+ および N- は，それぞれ正と負のノードです． 電流は，正のノードから電流源を通って，負のノードへと流れます． VNAM は，制御電流が流れている電圧源の名前です． 制御電流の正の方向は，VNAM の正のノードから電圧源を通り負のノードへ流れる方向です． VALUE は電流増幅率です．

3.2.2.4 電流制御線形電圧源

一般形:

HXXXXXXX N+ N- VNAM VALUE

例:

HX 5 17 VZ 0.5K

N+ および N- は，それぞれ正と負のノードです． VNAM は，制御電流が流れている電圧源の名前です． 制御電流の正の方向は，VNAM の正のノードから電圧源を通り負のノードへ流れる方向です． VALUE は相互抵抗(単位は $\Omega$ )です．

3.2.3 非線形依存電源

一般形:

BXXXXXXX N+ N- $\langle$ I=EXPR$\rangle$ $\langle$ V=EXPR$\rangle$

例:

B1 0 1 I=cos(v(1))+sin(v(2))
B1 0 1 V=ln(cos(log(v(1,2)^2)))-v(3)^4+v(2)^v(1)
B1 3 4 I=17
B1 3 4 V=exp(pi^i(vdd))

N+ は正のノード，N- は負のノードです． V, I パラメータの値により，それぞれ電圧源の電圧および電流源の電流が決まります． I が指定されている場合，この素子は電流源となり，V が指定されている場合，この素子は電圧源となります． これらのパラメータのうち1つのみを指定します．

非線形電源の小信号交流の振る舞いは，直流動作点におけるその電源の微係数を比例定数とした線形電源と同じです．

V および I に与える式は， システム中の電圧，および電圧源を通る電流の任意の関数にすることができます． 次の実数変数の関数が定義されています．

abs	asinh	cosh	sin
acos	atan	exp	sinh
acosh	atanh	ln	sqrt
asin	cos	log	tan

関数 u は単位ステップ関数であり，引数が0以上のとき値が1になり，引数が0未満のとき値が0になります． 関数 uramp は単位ステップ関数の積分で，引数を x とすると，x が0以下の場合に値が0となり，x が0を超える場合に値が x となります． これらの2つの関数は，部分部分の非線形関数を合成する際に役立ちますが，収束が悪くなることがあります．

次の標準的な演算子が定義されています．

+

-

*

/

^

単項 -

log, ln, sqrt の引数が0未満の場合，引数の絶対値が使われます． 除数あるいは log, ln の引数が0となった場合，エラーが生じます． 偏微分の関数の引数が定義域を外れると，その他の問題が生じることもあります．

時間を式に入れるには，定電流源の電流をコンデンサに積分し，その電圧を使います(コンデンサの初期電圧を忘れずに設定しておくこと)． 非線形の抵抗，コンデンサ，インダクタは，非線形依存電源によって合成できます． 非線形抵抗は自明です． 非線形コンデンサおよびインダクタは，対応する線形素子を使い，非線形依存電源によって生じる変数の変化により実現できます． 次のサブ回路は，非線形コンデンサを実現します．

.Subckt nlcap   pos neg
* Bx: f(input voltage) を計算する
Bx   1    0    v = f(v(pos,neg))
* Cx: 線形コンデンサ
Cx   2    0    1
* Vx: コンデンサに流れ込む電流を計測する電流計
Vx   2    1    DC 0Volts
* Cx に流れる電流を回路に反映する
Fx   pos  neg  Vx 1
.ends

非線形インダクタも同様です．

3.3 伝送線路

3.3.1 無損失伝送線路

一般形:

TXXXXXXX N1 N2 N3 N4 Z0=VALUE $\langle$ TD=VALUE$\rangle$ $\langle$ F=FREQ $\langle$ NL=NRMLEN$\rangle$ $\rangle$
+ $\langle$ IC=V1, I1, V2, I2$\rangle$

例:

T1 1 0 2 0 Z0=50 TD=10NS

N1 および N2 はポート1のノード，N3 および N4 はポート2のノードです． Z0 は特性インピーダンスです． 伝送線路の長さは2つの形式のどちらかで指定します． 伝送遅延 TD は，直接(例えば TD=10ns)指定できます． または，周波数 F と，周波数 F における伝送線路内の波長によって基準化した電気長 NL を指定することもできます． 周波数が指定され，NL が省略された場合，0.25が仮定されます(すなわち，周波数の1/4波長となります)． 線路長を表わすどちらの形式もオプションですが，どちらか一方を指定する必要があります．

この要素は，1つの伝送モードのみをモデル化しています． 実際の回路で4つのノードすべてが異なっている場合，2つのモードが励起されることがあります． そのような状況をシミュレートするには，2つの伝送線路が必要になります． (より詳しい説明は付録Aの例を参照のこと．)

(オプションの)初期条件の指定は，伝送線路の各ポートの電圧と電流により行ないます． 初期条件が指定された場合，.TRAN 制御行で UIC オプションが指定されている場合「のみ」適用されます．

注意：損失が0の有損失伝送線路(下記参照)は，実現の詳細のため，無損失伝送線路よりも正確です．

3.3.2 有損失伝送線路

一般形:

OXXXXXXX N1 N2 N3 N4 MNAME

例:

O23 1 0 2 0 LOSSYMOD
OCONNECT 10 5 20 5 INTERCONNECT

これは2ポートの単一導体有損失伝損線路の畳み込みモデルです． N1 と N2 はポート1のノード，N3 と N4 はポート2のノードです． 注意：損失が0の有損失伝送線路は，実現の詳細のため，無損失伝送線路よりも正確です．

3.3.3 有損失伝送線路モデル(LTRA)

一様RLC/RC/LC/RG伝送線路モデル(以後LTRAモデルと呼ぶ)は，一様定数分布伝送線路をモデル化しています． RCおよびLCは，さらにURCおよびTRAモデルによりモデル化されています． しかし，さらに新しいLTRAモデルは，他のモデルと比べると通常より速く，より正確です． LTRAモデルの動作は，伝送線路のインパルス応答の入力に関する畳み込みに基づいています([8]を参照のこと)．

LTRAモデルは，いくつかのパラメータをとり，必須のパラメータとオプションのパラメータがあります．

名前	パラメータ	単位/種別	省略時の値	例
R	抵抗/長さ	Z/unit	0.0	0.2
L	インダクタンス/長さ	H/unit	0.0	9.13e-9
G	コンダクタンス/長さ	$\mho$ /unit	0.0	0.0
C	静電容量/長さ	F/unit	0.0	3.65e-12
LEN	伝送線の長さ		なし	1.0
REL	ブレークポイントの制御	任意	1	0.5
ABS	ブレークポイントの制御		1	5
NOSTEPLIMIT	線路遅延未満に時間ステップを制限しない	フラグ	not set	set
NOCONTROL	複雑な時間ステップの制御を行なわない	フラグ	not set	set
LININTERP	線形補間を使う	フラグ	not set	set
MIXEDINTERP	2次補間に失敗したら線形補間を使う	フラグ	not set	set
COMPACTREL	ヒストリ圧縮のための特別なreltol		RELTOL	1.0e-3
COMPACTABS	ヒストリ圧縮のための特別なabstol		ABSTOL	1.0e-9
TRUNCNR	時間ステップの制御にNewton-Raphson法を使う	フラグ	not set	set
TRUNCDONTCUT	インパルス応答のエラーを低くするために時間ステップを制御しない	フラグ	not set	set

これまでに次の形式の伝送線路が実現されています： RLC (直列損失のみの一様伝送線路)，RC (一様RC伝送線路)，LC (無損失伝送線路)，RG (分布直列抵抗並列コンダクタンスのみ)． その他の組み合わせはエラーとなり，試すべきではありません． 伝送線路の長さ LEN を指定しなければなりません．

NOSTEPLIMIT は，RLCの場合に時間ステップを線路の遅延未満に制限するという省略時の制約を解除するフラグです． NOCONTROL は，RLCおよびRCの場合に畳み込みエラーの基準に基づく時間ステップの省略時の制限を解除するフラグです． これによりシミュレーションが速くなりますが，結果の精度が悪くなる場合があります． LININTERP は，遅延された信号を計算するのに，省略時の2次補間ではなく線形補間を使うフラグです． MIXEDINTERP は，2次補間が適切かどうか判断する基準を使い，適切でない場合は線形補間を使うよう指示するフラグです． 2次補間が適切な場合は2次補間が使われます． TRUNCDONTCUT は，インパルス応答関連の量を実際に計算するときのエラーを押さえるために省略時に行なわれる時間ステップの短縮化をやめるフラグです． COMPACTREL および COMPACTABS は，畳み込みのために保存されている過去の値のヒストリを制御する量です． これらに大きな値を指定すると，精度は低くなりますが，通常シミュレーションの速度が速くなります． これらの値は，.OPTIONS の節(4.1)で説明されている TRYTOCOMPACT オプションと共に使います． TRUNCNR は，時間ステップ制御ルーチンで，適切な時間ステップを決めるのに Newton-Raphson法を使うよう指示するフラグです． 省略時には，前の時間ステップを半分にして試してみる方法を使います． REL および ABS は，ブレークポイントの設定を制御する量です．

シミュレーションのスピードを速くするために，もっとも試す価値があるオプションは，REL です． 省略時の値1は，精度の観点からは通常安全ですが，ときどき計算時間が長くなることがあります． 2を超える値は，すべてのブレークポイントを排除し，精度の観点からは安全ではないことを念頭に置きつつ，回路の残りの部分の性質に身を任せることになります． 回路に鋭い非連続性がないと予測されれば，通常ブレークポイントをすべて取り除いて構いません． 0から1の値は，通常必要ありませんが，多くのブレークポイントを設定するために使います．

.OPTIONS 制御行で TRYTOCOMPACT が指定されている場合，COMPACTREL も試してみるとよいでしょう． 有効な値の範囲は0から1です． 大きな値を指定すると，シミュレーションの精度は低くなりますが，スピードが速くなる場合もあります． TRYTOCOMPACT が .OPTIONS 制御行に指定されていない場合，ヒストリの圧縮は行なわれず，精度は高くなります． NOCONTROL, TRUNCDONTCUT, NOSTEPLIMIT も精度を犠牲にしてスピードを速くする傾向があります．

3.3.4 一様分布RC線路

一般形:

UXXXXXXX N1 N2 N3 MNAME L=LEN $\langle$ N=LUMPS$\rangle$

例:

U1 1 2 0 URCMOD L=50U
URC2 1 12 2 UMODL l=1MIL N=6

N1 および N2 は，RC伝送線路が結んでいる2つのノードで，N3 はコンデンサがつながるノードです． MNAME はモデルの名前，LEN はRC伝送線路の長さ(単位は m )です． LUMPS は，RC伝送線路をモデル化するのに使う部分の個数です(このパラメータが省略された場合の動作については，モデルの説明を参照のこと)．

3.3.5 一様分布RC線路モデル(URC)

URCモデルは，L. Gertzberrgが1974年に提案したモデルから導いたものです． このモデルは，URC伝送線路をサブ回路的に展開して，内部的に生成されたノードを持つひとかたまりのRC部分が複数集まって構成されるネットワークにより構成されます． RC部分は，URC伝送線路の中央に向かって，公比が K の等比数列になっています． 使われる部分の数は，URC伝送線路素子で指定されなければ，次の式で決定されます．

N = $${\frac{{\log\biggl(\displaystyle F_{\it max} \frac{R}{L} \frac{C}{L} 2 \pi L^2 \Bigl( \frac{K - 1}{K} \Bigr)^2 \biggr)}}{{\log K}}}$$

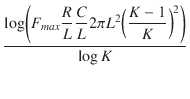
URC伝送線路は，ISPERL パラメータの値に非0を指定しなければ，抵抗とコンデンサの部分によってのみ構成されます． 非0の値を指定した場合，コンデンサの代わりに，ゼロバイアス時の接合容量が置き換える前の静電容量と等価で，伝送線路1m あたりの飽和電流が ISPERLAの逆バイアスのダイオードが使われます． オプションの RSPERL は1m メートルあたりの直列抵抗(単位 $\Omega$ )を指定します．

	名前	パラメータ	単位	省略時の値	例	面積
1	K	伝播定数	--	2.0	1.2	--
2	FMAX	最大周波数	Hz	1.0G	6.5Meg	--
3	RPERL	単位長あたりの抵抗	Z/m	1000	10	--
4	CPERL	単位長あたりの静電容量	F/m	1.0e-15	1pF	--
5	ISPERL	単位長あたりの飽和電流	A/m	0	--	--
6	RSPERL	単位長あたりのダイオード抵抗	Z/m	0	--	--

3.4 トランジスタ，ダイオード

ダイオード，BJT, FET, MES-FETで使われる面積係数は，指定されたモデルの等価並列素子の個数を決定します． これに影響されるパラメータには，後述するモデルの記述において「面積」の列にアスタリスクを付けてあります． チャネルおよびドレイン，ソースの拡散に関するいくつかの幾何的な係数は，MOSFETの素子行で指定できます．

ある素子には，2つの形式で初期状態を指定できます． 第一の形式は，2つ以上安定な状態がある回路の直流の収束を向上させます． 素子がOFFであると指定された場合，その素子の端子の電圧が0であるとして直流動作点が決定されます． 収束したら，その端子の電圧の値を正しく求めるために繰り返しを続けます． 回路に直流安定状態が2つ以上ある場合，OFF オプションを使って，望ましい状態に対応する解を得られます． 実際に素子が導通している場合に素子をOFFと指定すると，プログラムは(解が収束すると仮定して)正しい解を得ようとしますが，プログラムは2つ以上の別々の解に自力で収束しなければならないので，より多くの繰り返しが必要になります． .NODESET 制御行は OFF オプションと同様の目的に使えます． .NODESET オプションは使うのが簡単で，収束を助けるための好ましい手段です．

初期条件の2番目の形式は，過渡解析と共に指定するものです． これは，上述の収束を助ける方法とは異なり，本当の「初期条件」です． 初期条件の詳しい説明は，.IC 制御行(4.2.2節)と .TRAN 制御行(4.3.9節)の説明を参照のこと．

3.4.1 接合型ダイオード

一般形:

DXXXXXXX N+ N- MNAME $\langle$ AREA$\rangle$ $\langle$ OFF$\rangle$ $\langle$ IC=VD$\rangle$ $\langle$ TEMP=T$\rangle$

例:

DBRIDGE 2 10 DIODE1
DCLMP 3 7 DMOD 3.0 IC=0.2

N+ および N+ は，それぞれ正と負のノードです． MNAME はモデルの名前，AREA は面積係数，OFF はこの素子に対して直流解析をする際の(オプションの)初期条件です． 面積係数が省略された場合，1.0という値が仮定されます． IC=VD という(オプションの)初期条件の指定は， 静止動作点とは異なる状態から過渡解析を始めるために， .TRAN 制御行の UIC オプションと共に使います． (オプションの) TEMP 値は，この素子が動作する温度で，.OPTION 制御行の温度の指定よりも優先します．

3.4.2 ダイオードモデル(D)

ダイオードの直流特性は，パラメータ IS と N によって決定されます． 抵抗 RS のパラメータもあります． 電荷蓄積効果は，通過時間 TT と，パラメータ CJO, VJ, M によって定まる非線形の空乏層容量としてモデル化されています． 飽和電流の温度依存性は，エネルギーパラメータ EG と飽和電流指数パラメータ XTI によって定義されます． これらのパラメータが測定された名目温度は TNOM で，このパラメータの省略時の値は .OPTIONS 制御行で指定された回路全体の値です． 逆方向降伏は，逆方向のダイオードの電流が指数的に増加するようにモデル化されており，パラメータ BV および IBV (両者とも正の値)によって決定されます．

	名前	パラメータ	単位	省略時の値	例	面積
1	IS	飽和電流	A	1.0e-14	1.0e-14	*
2	RS	抵抗	Z	0	10	*
3	N	エミッション係数	--	1	1.0
4	TT	通過時間	sec	0	0.1ns
5	CJO	ゼロバイアス接合容量	F	0	2pF	*
6	VJ	接合電位	V	1	0.6
7	M	勾配係数	--	0.5	0.5
8	EG	活性化エネルギー	eV	1.11	1.11 Si
					0.69 Sbd
					0.67 Ge
9	XTI	飽和電流温度指数	--	3.0	3.0 jn
					2.0 Sbd
10	KF	フリッカ雑音係数	--	0
11	AF	フリッカ雑音指数	--	1
12	FC	順方向バイアス空乏層容量式の係数	--	0.5
13	BV	逆方向降伏電圧	V	$\infty$	40.0
14	IBV	降伏電圧時の電流	A	1.0e-3
15	TNOM	パラメータ測定温度	o C	27	50

3.4.3 バイポーラ接合型トランジスタ(BJTs)

一般形:

QXXXXXXX NC NB NE $\langle$ NS$\rangle$ MNAME $\langle$ AREA$\rangle$ $\langle$ OFF$\rangle$ $\langle$ IC=VBE, VCE$\rangle$ $\langle$ TEMP=T$\rangle$

例:

Q23 10 24 13 QMOD IC=0.6, 5.0
Q50A 11 26 4 20 MOD1

NC, NB, NE は，それぞれコレクタ，ベース，エミッタのノードです． NS は(オプションの)サブストレートノードです． 指定されていない場合，グラウンドが使われます． MNAME はモデルの名前，AREA は面積係数，OFF はこの素子に対してDC解析をする際の(オプションの)初期条件です． 面積係数が省略された場合，1.0という値が仮定されます． IC=VBE, VCE という(オプションの)初期条件の指定は，静止動作点とは異なる状態から過渡解析を始めるために，.TRAN 制御行の UIC オプションと共に使います． 過渡解析の初期条件を設定するよりよい方法については，.IC 制御行の説明(4.2.2節)を参照のこと． (オプションの) TEMP 値は，この素子が動作する温度で，.OPTION 制御行の温度の指定よりも優先します．

3.4.4 バイポーラ接合型トランジスタモデル(NPN/PNP)

Spiceのバイポーラ接合型トランジスタモデルは，Gummel and Poonの積分電荷制御モデルの改良です． この改良Gummel-Poonモデルは，元のモデルを拡張して，バイアスレベルが高いときのいくつかの効果を取り入れています． このモデルは，いくつかのパラメータが指定されていない場合，より単純なEbers-Mollモデルに自動的に簡略化されます． 改良Gummel-Poonモデルで使われるパラメータ名は，プログラムの利用者によりわかりやすいように，また物理的あるいは回路設計的な思考を反映するように選ばれています．

直流モデルは，順方向電流増幅率を決定するパラメータ IS, BF, NF, ISE, IKF, NE と，逆方向電流増幅率特性を決定するパラメータ IS, BR, NR, ISC, IKR, NC と，順領域および逆領域の出力コンダクタンスを決定する VAF と VAR により定義されます． 抵抗 RB, RC, RE というパラメータもあり，RB は電流に依存することもできます． ベースの電荷蓄積は，順方向および逆方向の通過時間 TF, TR (順方向通過時間 TF は必要ならバイアスに依存するようにできる)と，B-E接合は CJE, VJE, MJE によって，B-C接合は CJC, VJC, MJC によって，C-S (コレクタ-サブストレート)接合は CJS, VJS, MJS によって決定される非線形の空乏層容量によってモデル化されています． 飽和電流 IS の温度依存性は，エネルギーギャップ EG と飽和電流指数 XTI によって決定されます． さらに，新しいモデルでは，ベース電流の温度依存性は，ベータ温度指数 XTB によりモデル化されています． 指定された値は，温度 TNOM で測定されたと仮定されます． これは .OPTIONS 制御行で指定できますが，.MODEL 行で指定すればそちらが優先します．

改良Gummel-Poonモデルで使用されるBJTのパラメータを以下に示します． Spice2以前のバージョンのパラメータ名も受け付けます．

改良Gummel-Poon BJTパラメータ

	名前	パラメータ	単位	省略時の値	例	面積
1	IS	トランスポート飽和電流	A	1.0e-16	1.0e-15	*
2	BF	理想最大順方向ベータ	--	100	100
3	NF	順方向電流エミッション係数	--	1.0	1
4	VAF	順方向アーリー電圧	V	$\infty$	200
5	IKF	高電流順方向ベータ降下点	A	$\infty$	0.01	*
6	ISE	B-E漏洩飽和電流	A	0	1.0e-13	*
7	NE	B-E漏洩エミッション係数	--	1.5	2
8	BR	理想最大逆方向ベータ	--	1	0.1
9	NR	逆方向電流エミッション係数	--	1	1
10	VAR	逆方向アーリー電圧	V	$\infty$	200
11	IKR	高電流逆方向ベータ降下点	A	$\infty$	0.01	*
12	ISC	B-C漏洩飽和電流	A	0	1.0e-13	*
13	NC	B-C漏洩エミッション係数	--	2	1.5
14	RB	ゼロバイアスベース抵抗	Z	0	100	*
15	IRB	ベース抵抗が最小値との中間になる電流	A	$\infty$	0.1	*

	名前	パラメータ	単位	省略時の値	例	面積
16	RBM	高電流時の最小ベース抵抗	Z	RB	10	*
17	RE	エミッタ抵抗	Z	0	1	*
18	RC	コレクタ抵抗	Z	0	10	*
19	CJE	B-Eゼロバイアス空乏層容量	F	0	2pF	*
20	VJE	B-E固有電位	V	0.75	0.6
21	MJE	B-E接合指数係数	--	0.33	0.33
22	TF	理想順方向通過時間	sec	0	0.1ns
23	XTF	TF のバイアス依存係数	--	0
24	VTF	TF の VBC 依存を表わす電圧	V	$\infty$
25	ITF	TF に与える高電流の影響パラメータ	A	0		*
26	PTF	周波数 = 1.0/(TF x 2$\pi$) Hzにおける追加位相	deg	0
27	CJC	B-Cゼロバイアス空乏層容量	F	0	2pF	*
28	VJC	B-C固有電位	V	0.75	0.5
29	MJC	B-C接合指数係数	--	0.33	0.5
30	XCJC	内部ベースノードにつながるB-C空乏層容量の割合	--	1
31	TR	理想逆方向通過時間	sec	0	10ns
32	CJS	ゼロバイアスコレクタ-サブストレート容量	F	0	2pF	*
33	VJS	サブストレート接合固有電位	V	0.75
34	MJS	サブストレート接合指数係数	--	0	0.5
35	XTB	順方向および逆方向ベータ温度指数	--	0
36	EG	IS の温度効果に使われるエネルギーギャップ	eV	1.11
37	XTI	IS の温度効果の指数	--	3
38	KF	フリッカ雑音係数	--	0
39	AF	フリッカ雑音指数	--	1
40	FC	順バイアス空乏層容量式の係数	--	0.5
41	TNOM	パラメータ測定温度	o C	27	50

3.4.5 接合型FET (JFETs)

一般形:

JXXXXXXX ND NG NS MNAME $\langle$ AREA$\rangle$ $\langle$ OFF$\rangle$ $\langle$ IC=VDS, VGS$\rangle$ $\langle$ TEMP=T$\rangle$

例:

J1 7 2 3 JM1 OFF

ND, NG, NS は，それぞれドレイン，ゲート，ソースのノードです． MNAME はモデルの名前，AREA は面積係数，OFF はこの素子に対して直流 解析をする際の(オプションの)初期条件です． 面積係数が省略された場合，1.0という値が仮定されます． IC=VDS, VGS という(オプションの)初期条件の指定は，静止動作点とは異なる状態から過渡解析を始めるために，.TRAN 制御行の UIC オプションと共に使います． 過渡解析の初期条件を設定するよりよい方法については，.IC 制御行の説明(4.2.2節)を参照のこと． (オプションの) TEMP 値は，この素子が動作する温度で，.OPTION 制御行の温度の指定よりも優先します．

3.4.6 接合型FETモデル(NJF/PJF)

このJFETモデルは，Shichman and HodgesのFETモデルから導いたものです． 直流特性は，ゲート電圧に対するドレイン電流の変化を決定するパラメータ VTO, BETA と，出力コンダクタンスを決定する LAMBDA と，2つのゲート接合の飽和電流 IS により定義されます． 抵抗 RD と RS というパラメータもあります． 電荷蓄積は，2つのゲート接合について，非線形の空乏層容量によってモデル化されています． 空乏層容量は，接合電圧の -1/2 乗で変化し，パラメータ CGS, CGD, PB で定義されます．

Spice3fおよびそれ以降のバージョンでは， 調整パラメータ B が追加されました． 詳細は [9] を参照のこと．

	名前	パラメータ	単位	省略時の値	例	面積
1	VTO	しきい値電圧 (VTO )	V	-2.0	-2.0
2	BETA	相互コンダクタンスパラメータ(B )	A/V2	1.0e-4	1.0e-3	*
3	LAMBDA	チャネル長調整パラメータ(L )	1/V	0	1.0e-4
4	RD	ドレイン抵抗	Z	0	100	*
5	RS	ソース抵抗	Z	0	100	*
6	CGS	ゼロバイアスG-S接合容量(Cgs )	F	0	5pF	*
7	CGD	ゼロバイアスG-D接合容量(Cgd )	F	0	1pF	*
8	PB	ゲート接合電位	V	1	0.6
9	IS	ゲート接合飽和電流(IS )	A	1.0e-14	1.0e-14	*
10	B	ドーピング広がりパラメータ	--	1	1.1
11	KF	フリッカ雑音係数	--	0
12	AF	フリッカ雑音指数	--	1
13	FC	順方向バイアス空乏層容量式の係数	--	0.5
14	TNOM	パラメータ測定温度	o C	27	50

3.4.7 MOSFET

一般形:

MXXXXXXX ND NG NS NB MNAME $\langle$ L=VAL$\rangle$ $\langle$ W=VAL$\rangle$ $\langle$ AD=VAL$\rangle$ $\langle$ AS=VAL$\rangle$
+ $\langle$ PD=VAL$\rangle$ $\langle$ PS=VAL$\rangle$ $\langle$ NRD=VAL$\rangle$ $\langle$ NRS=VAL$\rangle$ $\langle$ OFF$\rangle$
+ $\langle$ IC=VDS, VGS, VBS$\rangle$ $\langle$ TEMP=T$\rangle$

例:

M1 24 2 0 20 TYPE1
M31 2 17 6 10 MODM L=5U W=2U
M1 2 9 3 0 MOD1 L=10U W=5U AD=100P AS=100P PD=40U PS=40U

ND, NG, NS, NB は，それぞれドレイン，ゲート，ソース，バルク(サブストレート)ノードです． MNAME はモデルの名前です． L, W は，チャネルの長さと幅です(単位 m )． AD および AS は，ドレインとソースの拡散領域の面積です(単位 m² )． U という接尾子は $\mu$m ( 10^-6 m )で，p は $\mu$m² ( 10^-12 m² )です． L, W, AD, AS のいずれかが指定されなかった場合，省略時の値が使われます． 省略時の値を使うと，入力ファイルの表現が簡単になるだけでなく，素子の寸法を変更する際の編集も簡単になります． PD および PS は，ドレインとソースの接合の周囲の長さです(単位 m )． NRD および NRS は，ドレインおよびソースの拡散の等価的な「ます」の数を指定します． これらの値は，各トランジスタの寄生直列ドレイン，ソース抵抗を正確に表わすため，.MODEL 制御行のシート抵抗 RSH に掛かります． PD, PS の省略時の値は0.0で，NRD, NRS の省略時の値は1.0です． OFF はこの素子に対して直流解析をする際の(オプションの)初期条件です． IC=VDS, VGS, VBS という(オプションの)初期条件の指定は，静止動作点とは異なる状態から過渡解析を始めるために，.TRAN 制御行の UIC オプションと共に使います． 過渡解析の初期条件を設定するよりよい方法については，.IC 制御行の説明(4.2.2節)を参照のこと． (オプションの) TEMP 値は，この素子が動作する温度で，.OPTION 制御行の温度の指定よりも優先します．

温度の指定は，レベル1, 2, 3, 6のMOSFET「のみ」有効で，レベル4, 5 (BSIM)素子には使えません．

3.4.8 MOSFETモデル(NMOS/PMOS)

Spiceは，I-V特性の定式化が異なる4つのMOSFET素子モデルを提供します． 変数 LEVEL により使うモデルを指定します．

LEVEL=1	$&rarr#rightarrow;$	Shichman-Hodges
LEVEL=2	$&rarr#rightarrow;$	MOS2 ([1] で記述されている)
LEVEL=3	$&rarr#rightarrow;$	MOS3, 半経験的モデル([1] を参照)
LEVEL=4	$&rarr#rightarrow;$	BSIM ([3] で記述されている)
LEVEL=5	$&rarr#rightarrow;$	新しいBSIM (BSIM2; [5] で記述されている)
LEVEL=6	$&rarr#rightarrow;$	MOS6 ([2] で記述されている)

レベル1からレベル3のMOSFETの直流特性は，素子のパラメータ VTO, KP, LAMBDA, PHI, GAMMA により定義されています． これらのパラメータは，プロセスのパラメータ(NSUB, TOX など)が与えられている場合，Spiceによって計算されますが，利用者が指定した値が優先されます． エンハンスメント型のN-チャネル(P-チャネル)素子の場合，VTO は正(負)で，デプレッション型の場合 VTO は負(正)です． 電荷蓄積は，重複容量を表わす3つの定容量 CGSO, CGDO, CGBO と，ゲート，ソース，ドレイン，バルク領域に分布する非線形の酸化物薄膜容量と，底部と周辺部に別れた2つのサブストレート接合の非線形の空乏層容量(それぞれ接合電圧の MJ 乗，MJSW 乗で変化する)によりモデル化され， パラメータ CBD, CBS, CJ, CJSW, MJ, MJSW, PB によって決定されます． 電荷蓄積効果は，Meyerが提案した不連続線形電圧依存容量モデルによりモデル化されています． LEVEL=1 モデルでは，酸化物薄膜の電荷蓄積効果は，少し異なる形で扱われます． これらの電圧依存の容量は，入力の記述に TOX が指定された場合のみ含まれ，Meyerの式を用いて表わされます．

接合を表わすパラメータがいくつか重複しています． たとえば，逆方向電流は IS (単位 A)または JS (単位 A/m² )のいずれかで入力できます． 前者は絶対的な値であり，後者は AD または AS が掛けられて，それぞれドレイン，ソース接合の逆方向電流となります． 面積は省略時の値にすることができ，この素子の行で入力された AD, AS と接合の特徴を常に関連づけるのは意味がないので，この手法が選ばれました． 同様な考え方は，ゼロバイアス接合容量 CBD, CBS (単位 F)，と CJ (単位 F/m² )にも当てはまります． 寄生直列ドレイン，ソース抵抗は，RD, RS (単位 $\Omega$ )，または RSH (単位 $\Omega$ /ます)で指定できます． 後者は，この素子の行で入力されたますの数 NRD, NRS 倍されます．

KAPPA パラメータに関するレベル3モデルの不連続性が発見されました([10] を参照のこと)． 提供された修正は，Spice3f2およびそれ以降のバージョンで実装されています． この修正によりパラメータのあてはめが影響される可能性があるため，古い実装を使うオプション BADMOS3 を設定することができます(シミュレーション変数と .OPTIONS 行の4.1節を参照のこと)． Spiceのレベル1, 2, 3, 6のパラメータは，

	名前	パラメータ	単位	省略時の値	例
1	LEVEL	モデルの番号	--	1
2	VTO	ゼロバイアスしきい値電圧(VTO )	V	0.0	1.0
3	KP	相互コンダクタンスパラメータ	A/V2	2.0e-5	3.1e-5
4	GAMMA	バルクしきい値パラメータ	V1/2	0.0	0.37
5	PHI	表面電位(U )	V	0.6	0.65
6	LAMBDA	チャネル長調整(MOS1とMOS2のみ) (L )	1/V	0.0	0.02
7	RD	ドレイン抵抗	Z	0.0	1.0
8	RS	ソース抵抗	Z	0.0	1.0
9	CBD	ゼロバイアスB-D接合容量	F	0.0	20fF
10	CBS	ゼロバイアスB-S接合容量	F	0.0	20fF
11	IS	バルク接合飽和電流(IS )	A	1.0e-14	1.0e-15
12	PB	バルク接合電位	V	0.8	0.87
13	CGSO	チャネル幅1m あたりのゲート-ソース重複容量	F/m	0.0	4.0e-11
14	CGDO	チャネル幅1m あたりのゲート-ドレイン重複容量	F/m	0.0	4.0e-11
15	CGBO	チャネル幅1m あたりのゲート-バルク重複容量	F/m	0.0	2.0e-10
16	RSH	ドレインとソースの拡散シート抵抗	Z/[]	0.0	10.0
17	CJ	接合領域1m2 あたりのゼロバイアスバルク接合底部容量	F/m2	0.0	2.0e-4
18	MJ	バルク接合底部勾配係数	--	0.5	0.5
19	CJSW	接合周囲1m あたりのゼロバイアスバルク接合側壁容量	F/m	0.0	1.0e-9
20	MJSW	バルク接合側壁勾配係数	--	0.50 (レベル1)
				0.33 (レベル2, 3)
21	JS	接合領域1m2 あたりのバルク接合飽和電流	A/m2		1.0e-8
22	TOX	酸化膜の厚さ	m	1.0e-7	1.0e-7
23	NSUB	サブストレートのドーピング	1/cm3	0.0	4.0e15
24	NSS	表面準位密度	1/cm2	0.0	1.0e10
25	NFS	高速表面準位密度	1/cm2	0.0	1.0e10

	名前	パラメータ	単位	省略時の値	例
26	TPG	ゲートの材質	--	1.0
		+1 サブストレートと逆
		-1 サブストレートと同じ
		0 Alゲート
27	XJ	冶金的な接合の深さ	m	0.0	1M
28	LD	横方向拡散	m	0.0	0.8M
29	UO	表面移動度	cm2 /Vs	600	700
30	UCRIT	移動度低下の臨界電界(MOS2のみ)	V/cm	1.0e4	1.0e4
31	UEXP	移動度低下の臨界電界係数(MOS2のみ)	--	0.0	0.1
32	UTRA	横方向電界係数(移動度)(MOS2にはない)	--	0.0	0.3
33	VMAX	キャリアの最大ドリフト速度	m /s	0.0	5.0e4
34	NEFF	総チャネル電荷(固定および移動)係数(MOS2のみ)	--	1.0	5.0
35	KF	フリッカノイズ係数	--	0.0	1.0e-26
36	AF	フリッカノイズ指数	--	1.0	1.2
37	FC	順方向バイアス空乏層容量式の係数	--	0.5
38	DELTA	しきい値電圧の幅効果(MOS2, MOS3)	--	0.0	1.0
39	THETA	移動度調整(MOS3のみ)	1/V	0.0	0.1
40	ETA	静電フィードバック(MOS3のみ)	--	0.0	1.0
41	KAPPA	飽和電界係数(MOS3のみ)	--	0.2	0.5
42	TNOM	パラメータ測定温度	o C	27	50

レベル4およびレベル5 (BSIM1, BSIM2)のパラメータは，プロセスの仕様からすべて得られ，自動的に生成されます． J. Pierret [4] は，「プロセス」のファイルを生成する手段を説明しています． Spice3と共に提供されているプログラムProc2Modは，このファイルを変換して，Spiceの入力ファイルに取り込むのに適した一連のBSIM1の .MODEL 行にします． 以下でl/wの列に * が付けられたパラメータには，長さと幅に依存する対応するパラメータが存在します． たとえば，VFB は単位がVの基本的なパラメータで，LVFB と WVFB というパラメータが存在し，その単位は V-m です． 次式，

L_{$\it effective$} = L_{$\it input$} - $$\it DL$$

および

W_{$\it effective$} = W_{$\it input$} - $$\it DW$$

のように指定された実際の素子のパラメータを評価するために， 次の式，

P = P₀ + $${\frac{{P_L}}{{L_{\it effective}}}}$$ + $${\frac{{P_W}}{{W_{\it effective}}}}$$

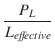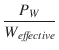
が使われます．

Spiceの他のモデルとは異なり，BSIMモデルはすべてのパラメータを提供するプロセス設計システムと共に使うように設計されているので，パラメータに省略時の値はなく，一つでも指定を忘れるとエラーとなります． パラメータの組の例とプロセスファイルのフォーマットに関しては，Spice2実装ノート [3] を参照のこと．

BSIM2に関しては，参考文献 [5] を参照のこと．

Spice BSIM (レベル4)パラメータ

名前	パラメータ	単位	l/w
VFB	フラットバンド電圧	V	*
PHI	表面逆転電位	V	*
K1	本体効果係数	V1/2	*
K2	ドレイン/ソース空乏層電荷共有係数	--	*
ETA	ゼロバイアスドレイン誘導バリア低下係数	--	*
MUZ	ゼロバイアス移動度	cm2 /V-s
DL	チャネルの短化	mm
DW	チャネルの狭化	mm
U0	ゼロバイアス横方向電界移動勾配係数	V-1	*
U1	ゼロバイアス速度飽和係数	mm /V	*
X2MZ	Vds = 0 のときのサブストレートバイアスに対する移動度の感応度	cm2 /V2 -s	*
X2E	サブストレートバイアスに対するドレイン誘導バリア低下効果の感応度	V-1	*
X3E	Vds = Vdd のときのドレインバイアスに対するドレイン誘導バリア低下効果の感応度	V-1	*
X2U0	サブストレートバイアスに対する横方向電界移動度勾配効果の感応度	V-2	*
X2U1	サブストレートバイアスに対する速度飽和効果の感応度	mm V-2	*
MUS	ゼロサブストレートバイアスおよび Vds = Vdd のときの移動度	cm2 /V2 -s
X2MS	Vds = Vdd のときのサブストレートバイアスに対する移動度の感応度	cm2 /V2 -s	*
X3MS	Vds = Vdd のときのドレインバイアスに対する移動度の感応度	cm2 /V2 -s	*
X3U1	Vds = Vdd のときのドレインバイアスに対する速度飽和の感応度	mm V-2	*
TOX	ゲート酸化物の厚さ	mm
TEMP	パラメータ測定時の温度	o C
VDD	測定バイアスの範囲	V
CGDO	チャネル幅1m あたりのゲート-ドレイン重複容量	F/m
CGSO	チャネル幅1m あたりのゲート-ソース重複容量	F/m
CGBO	チャネル長1m あたりのゲート-バルク重複容量	F/m
XPART	ゲート酸化物容量電荷モデルフラグ	--
N0	ゼロバイアスしきい値下傾斜係数	--	*
NB	サブストレートバイアスに対するしきい値下傾斜の感応度	--	*
ND	ドレインバイアスに対するしきい値下傾斜の感応	--	*
RSH	ドレインとソースの拡散シート抵抗	Z/[]
JS	ソースドレイン接合電流密度	A/m2
PB	ソースドレイン接合の固有電位	V
MJ	ソースドレイン接合の勾配係数	--
PBSW	ソースドレイン接合側壁の固有電位	V
MJSW	ソースドレイン接合側壁の勾配係数	--
CJ	単位面積あたりのソースドレイン接合容量	F/m2
CJSW	単位長あたりのソースドレイン接合側壁容量	F/m
WDF	ソースドレイン接合の省略時の幅	m
DELL	ソースドレイン接合長の減少	m

XPART=0 は，飽和時にドレイン/ソースの電荷を40/60に分割する指定で，XPART=1 は，ドレイン/ソースの電荷を0/100に分割する指定です．

3.4.9 MESFET

一般形:

ZXXXXXXX ND NG NS MNAME $\langle$ AREA$\rangle$ $\langle$ OFF$\rangle$ $\langle$ IC=VDS, VGS$\rangle$

例:

Z1 7 2 3 ZM1 OFF

ND, NG, NS は，それぞれドレイン，ゲート，ソースのノードです． MNAME はモデルの名前，AREA は面積係数，OFF はこの素子に対して直流解析をする際の(オプションの)初期条件です． 面積係数が省略された場合，1.0という値が仮定されます． IC=VDS, VGS という(オプションの)初期条件の指定は， 静止動作点とは異なる状態から過渡解析を始めるために， .TRAN 制御行の UIC オプションと共に使います． 過渡解析の初期条件を設定するよりよい方法については，.IC 制御行の説明(4.2.2節)を参照のこと．

3.4.10 MESFETモデル(NMF/PMF)

このMESFETモデルは，[11] で記述されているStatz et al. のGaAs FETモデルから導いたものです． 直流特性は，ゲート電圧に対するドレイン電流の変化を決定するパラメータ VTO, B, BETA と，飽和電圧を決定する ALPHA と，出力コンダクタンスを決定する LAMBDA により定義されます． これは，次の式によって定義されます．

I_d = $$\cases{ \displaystyle \frac{B(V_{gs}-V_T)^2}{1+b(V_{gs}-V_T)} \b... ...(V_{gs}-V_T)} (1 + L V_{ds}) & for $V_{ds} > \displaystyle \frac{3}{A}$\ \cr}$$

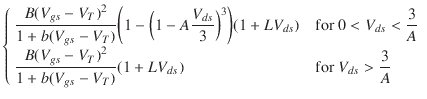
2つの抵抗 RD と RS のパラメータもあります． 電荷蓄積は，ゲート-ドレイン電圧およびゲート-ソース電圧の関数としての総ゲート容量によりモデル化されており，パラメータ CGS, CGD, PB により定義されます．

	名前	パラメータ	単位	省略時の値	例	面積
1	VTO	ピンチオフ電圧	V	-2.0	-2.0
2	BETA	相互コンダクタンスパラメータ	A/V2	1.0e-4	1.0e-3	*
3	B	ドーピング広がり拡張パラメータ	1/V	0.3	0.3	*
4	ALPHA	飽和電圧パラメータ	1/V	2	2	*
5	LAMBDA	チャネル長調整パラメータ	1/V	0	1.0e-4
6	RD	ドレイン抵抗	Z	0	100	*
7	RS	ソース抵抗	Z	0	100	*
8	CGS	ゼロバイアスG-S接合容量	F	0	5pF	*
9	CGD	ゼロバイアスG-D接合容量	F	0	1pF	*
10	PB	ゲート接合電位	V	1	0.6
11	KF	フリッカ雑音係数	--	0
12	AF	フリッカ雑音指数	--	1
13	FC	順バイアス空乏層容量式の係数	--	0.5