出力段のバイアスは -30 V 程度ですので,波高値で 40 V 程度の出力を楽に取り出せなければなりません.
出力段のプレート供給電圧は
250 V + ![]() ですので,
出力段のグリッド抵抗(交流負荷)を考えると,
高
ですので,
出力段のグリッド抵抗(交流負荷)を考えると,
高 ![]() の3極管を用いてもけっこう厳しいものがあります.
の3極管を用いてもけっこう厳しいものがあります.
ここでは,手持ちの5751を用いることにします. プレート電流は2本で 1 mA とし,定電流ダイオードを使用します. 検討の結果,プレート負荷抵抗および出力段のグリッド抵抗を共に 270 kΩ としました. したがって,交流負荷抵抗は 135 kΩ です. 出力段が固定バイアスの場合もあるため,グリッド抵抗は低くすべきですが, ここではあくまでも実験で,短時間しか稼働させないということで, 高めの値を使い,ゲインの低下を避けています.
電圧増幅段の回路を図1に示します.
電圧増幅段のロードラインは,図2のようになります.
仮に
Eg > -0.5 V の部分はグリッド電流が流れて使えないとしても,
波高値で 40 V 程度の出力が得られそうです.
この動作点のグリッドバイアスは
Eg0 = - 1.374 V で,
三定数は ![]() = 71.1,
rp = 63.3 kΩ,
gm = 1120 μS です.
ゲイン A は,
= 71.1,
rp = 63.3 kΩ,
gm = 1120 μS です.
ゲイン A は,
A = 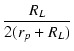 = 71.1 = 71.1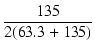 = 24.2 = 24.2
|
(1) |
回路図を図3に示します.
動作点を Ep0 = 250 V, Ip0 = 41.67 mA として, 6CK4のプレート特性図にロードラインを引いてみます(図4). このときのグリッドバイアスは Eg0 = - 27.73 V ですから, A1級で動作させる場合, グリッド電圧が 0 V から -55.46 V の範囲でスイングできます.
負荷インピーダンスが Zp = 3203 Ω のロードライン1は直線AOB, Zp = 2524 Ω のロードラインは直線A'OB', Zp = 4591 Ω のロードラインは直線A''OB'' となります. Zp = 2.5 kΩ の場合は,点B'がカットオフに近づくため, 歪みが大きくなります. また, Zp = 4.6 kΩ の場合,グリッドを負に振り込んでも プレート電流が 10 mA 以上流れているので,出力が少なくなりそうです.
これを数値で検証してみましょう. 出力 Po は,簡易的には次の式で算出できます.
Po = 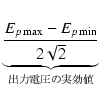 . . 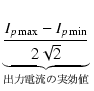 = = |
(2) |
|
Po3.2k = |
(3) |
|
Po2.5k = |
(4) |
|
Po4.6k = |
(5) |
歪率は,シングルの場合,2次歪みの成分が大勢を占めているので, 次の式で簡易的に計算できます.
K = 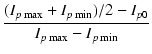
|
(6) |
K3.2k = 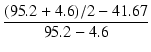 = 9.10 [%] = 9.10 [%]
|
(7) |
K2.5k = 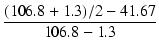 = 11.7 [%] = 11.7 [%]
|
(8) |
K4.6k = 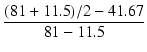 = 6.58 [%] = 6.58 [%]
|
(9) |
実験で確認できるのは,この3とおりの負荷インピーダンスの場合のみですが, パソコンを使えば,さまざまな負荷インピーダンスについて 出力と高調波歪みを計算することが簡単にできます. ここでは,波高値 | Eg0| の正弦波を T/64 (T は正弦波の周期)で標本化した入力に対するプレート電流を計算し, その波形をFFT (高速フーリエ変換)して歪率を求めます. 負荷インピーダンスは, 1 kΩ から 10 kΩ の範囲で変化させました. 結果は,図5のとおりです. 負荷インピーダンスが 3 kΩ 近辺で,3次歪みがなくなるポイントがありますが, そこでは2次歪みがかなり多いので , 3.5 kΩ から 4 kΩ あたりが適切なようです.
回路図を図6に示します.
動作点をA級シングルと同じ Ep0 = 250 V, Ip0 = 41.67 mA として, 6CK4のプレート特性図に Zpp = 6.4 kΩ のロードラインを引いてみます(図7).
負荷インピーダンスが Zpp = 6.4 kΩ のときの合成ロードラインは, 点A (Ep0, 0) を通り傾きが -1/(Zpp/4) の直線(青い線)です. 各球のロードラインは,それぞれ曲線A1O1B1と曲線A2O2B2です(水色の線). 出力は,合成プレート特性(緑色の線)と合成ロードラインの交点の最大電流を Ip max とすれば,
Po = ![$\displaystyle \underbrace{{\frac{I_{p\max}}{\sqrt{2}}}}_{{\makebox[0pt]{\scriptsize 合成出力電流の実効値}}}^{}\,$](img22.png) |
(10) |
Po6.6k = 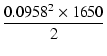 = 7.58 [W] = 7.58 [W]
|
(11) |
同様に, Zpp = 5 kΩ の場合のロードラインを図8に, Zpp = 9.4 kΩ の場合のロードラインを図9に示します.
シングルの場合と同様に,さまざまな負荷インピーダンスに対して, 出力と歪率を求めた結果を図10に示します. プッシュプルの場合,負荷インピーダンスを低くしても,それほど歪率が悪化しません. 逆に,負荷インピーダンスを高くすると,急速に出力が減ってしまいます. 出力を重視するなら, 5 kΩ 程度が最適なようです.
回路図を図11に示します.
定電流回路は,簡単に済ませるためNJM317を使っています. R92 は電流値を設定する抵抗で,NJM317はOUT-ADJ端子間の電位差が 1.25 V になるように電流を制御するので,この回路の定電流値は 1.25/15 = 0.08333 A となります. R91 はNJM317の損失を軽くするとともに, 渋谷@山奥さんの忠告にしたがって入れた発振を防ぐための抵抗です. プレート電流検出用抵抗 R7 と R8 は, これまで 1 Ω を使ってきましたが, 雑音を拾うようなので,10 Ω に変更しました. 供給電圧を 280 V 程度にすれば,プレート電圧が 250 V になるでしょう.
図12に差動出力段のロードラインを示します. 青色の線は,対アースのプレート電圧とプレート電流の関係を表したロードラインで, 供給電圧 Ebb = Ep0 - Eg0 = 250 + 27.7 = 277.7 V を通る 傾き -1/(Zpp/2) の直線です. 水色の線が通常の意味でのカソードを基準とした差動のロードラインです. 水色の線と青色の線の間隔は,カソード電圧です. 動作点から離れるにしたがい,青色の線と水色の線が離れていますが, それだけ,カソードの電位が上昇していることを示しています.
Zpp = 5 kΩ と Zpp = 6.4 kΩ の場合, グリッド電圧が 0 V に達する前に Ip max = 2Ip0 の制限にかかってしまいます.このとき,もう一方の球はカットオフしています. Zpp = 9.4 kΩ の場合は,負荷インピーダンスが高すぎて, カットオフする前に Eg = 0 となってしまい,クリップが発生することが予想されます.
ある動作点が与えられたとき,差動出力段で最大出力を得るためには,
Eg0 = 0 V の曲線と,
Ip = Ip max = 2Ip0 との交点を通るように
ロードラインを引けばよいことになります.
6CK4の場合,
Ip0 = 41.67 mA とすると,
Eg0 = 0 V と
Ip = 83.34 mA の交点は
Ep = 70.8 V ですから,
このときのカソード電圧の上昇を 5 V とすれば,
| = | 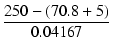 |
(12) | |
| Zpp | = | 8361 [Ω] | (13) |
出力の計算には,差動のロードラインで最大電流(Ip max)を求め,
そこから水平線を引き,青色のロードラインと交わった点の電圧(Eo min)を使います.
Zpp = 5 kΩ と
Zpp = 6.4 kΩ の場合,
Ip max = 2Ip0 ですから,出力は,
| Eo min 5k | = | Ebb - Ip0 |
(14) |
| Po5k | = | 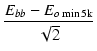 . . |
|
| = | (Ebb - Eo min 5k)Ip0 = (277.7 - 174.1)0.04167 = 4.32 [W] | (15) | |
| Eo min 6.4k | = | Ebb - Ip0 |
(16) |
| Po6.4k | = | (Ebb - Eo min 6.4k)Ip0 = (277.7 - 145.3)0.04167 = 5.52 [W] | (17) |
| Eo min 9.4k | = | Ebb - (Ip max - Ip0) |
(18) |
| Po9.4k | = | (Ebb - Eo min 9.4k)(Ip max - Ip0) = (277.7 - 100.4)(0.07943 - 0.04167) = 6.69 [W] | (19) |
フルスイング時にカソード電圧がどれだけ上昇するかは, 難しい計算をしなくてもわかります. 図13に2本の出力管のカソード電圧とグリッド電圧の関係を示します. (a)の無信号時には,カソードの電位はKで,グリッドの電位G1, G2はGNDと等しく, グリッド電圧は Eg1, Eg2 になります. 信号が加わると(b)のようになります. 信号はGNDを中心に正負対称に加えられます. 最大出力が得られる動作点と負荷インピーダンスの場合, フルスイング時には一方の球はクリップし,もう一方の球はカットオフします. その時の状態は,(c)のようになり, 一方のグリッドの電位はカソードの電位となって,グリッド電圧が Eg = 0 となります. 入力電圧 ei1 は,カソードの電位 Ek max と等しくなります. もう一方の球には ei2 = - ei1 の入力が加えられ, グリッド電圧は Eg2 = - 2ei1 = - 2Ek max となります. このグリッド電圧でカットオフするように動作点を選んでいるので, 最大入力時のカソードの電位は, Ek max = | Egcutoff|/2 となります. したがって,カソード電位の上昇は | Egcutoff|/2 - Ek0 となります.
負荷インピーダンスを変化させ,最大出力と歪率を求めた結果を図14に示します. 実際には,カットオフまでスイングさせることはきわめて困難なので, ここでは Eg = 0 V または Ip min = 2 mA になるまで入力を加えた場合の出力と歪率を計算しました. 差動出力段の場合,最大出力を得るのに必要な入力電圧は一定ではないので, これもグラフ中にEinとして示しておきました. カットオフが先に起こる場合は, Eg = 0 V になるまで入力を与えることができないため, 入力電圧の大きさ(波高値)はバイアス電圧よりも小さくなります. 負荷インピーダンスを高くしていくと,クリップが先に起こるようになりますが, 負荷インピーダンスが高いほど,ロードラインがカットオフの領域を通らなくなり, 波形の上下の平衡がとれてくるので,カソード電圧の上昇が少なくなり, その分だけ Eg = 0 V にするための入力が少なくて済むようになります.
カットオフが先に起こる Zpp < 9 kΩ の場合は, 式(20)より出力と負荷インピーダンスは比例します. この曲線を図14に破線で示しておきましたが, この曲線より実線の出力が大きいのは, 波形がつぶれる方向の3次歪みが含まれているからです. 負帰還をかければ,歪みが減り,破線の出力に近くなります.
クリップが先に起こる Zpp > 9 kΩ の場合は, ほぼA級プッシュプルの場合と同じような傾向を示しますが, 歪みがA級プッシュプルより少ないのは, 差動によりリニアリティが良くなっているからです. 出力がA級プッシュプル(点線で示してあります)よりも大きくなっています. A級プッシュプルでは一方の球が大きな電流を流しても,もう一方がカットオフに至らず, お互いにうち消し合いが生じます. この結果,出力信号電圧の振幅を決定する合成プレート特性と合成ロードラインの交点が,差動と比べると右下になってしまい,出力信号電圧・電流とも減ってしまいます. 興味深いことに, Zpp = 11.4 kΩ 付近で,THDが最小になるポイントが存在します.
差動出力段の片側の伝達特性を図15に示します. 横軸は入力電圧で,縦軸がプレート電流です. カットオフが先に起こる領域では,大振幅時に波形がつぶれるのがわかります. クリップが先に起こる領域では,直線性が非常に良くなっています.
次に,プレート損失を PD = 10.42 W 一定として, プレート電圧を変化させ, 最大出力が得られる負荷インピーダンスと歪率を求めてみました. 今回は,フルスイング時のグリッド電圧を Eg = - 0.5 V とし, Ip min = 4 mA という条件で求めています. 結果を,図16に示します. プレート電圧を高くするにしたがい,負荷抵抗を高くする必要がありますが, 出力も多く取れ,歪率も下がります. 6CK4の場合,出力トランスの特性が許す限り高いインピーダンスの負荷を与えて動作させるほうがよいようです.
ここで,シングル,A級プッシュプル,差動出力段の負荷インピーダンスと出力の比較をしてみます. 図17では,シングルの出力を2倍にしてプロットしています.
シングルとA級プッシュプルを比較すると, 出力のカーブの形状は似ていますが,プッシュプルのほうが常に上に位置しており, シングルの2倍以上の出力が期待できます. また,シングルと比べると歪みが少ないので, より低い負荷を与えれば,さらに大きな出力が得られます.
差動出力段の場合は,クリップが起きるように負荷インピーダンスを高く設定すれば, A級プッシュプル以上の出力が得られます. またその場合,歪率もA級プッシュプルより低くなります. 負荷インピーダンスを低くすると,クリップする前にカットオフしてしまい, 得られる出力は急激に減ってしまいます.
掲示板で議論していたのは Zpp = 6.6 kΩ の場合ですから, 差動出力段の出力はA級プッシュプルの出力をかなり下回るであろうことが予想されます.
これらの結果は,6CK4を使用して,ここで検討した動作点でのみ言えることであり,他の真空管や動作点の場合には必ずしもこのような結果になるとは限りません.
B電源は,手持ちの6080による安定化電源を用いることにします.
A電源とC電源を別途用意しなければなりませんが, できるだけ安くあげるために,ヒーターを 12.6 V で点火することにし, C電源は 12.6 V を3倍圧整流して約 -45 V を得ることにします. また初段定電流用の負電源は,6.3 V 巻線を半波整流して得ることにします. ヒータートランスは,6.3 V 2 A 巻線が2つある, ノグチトランスのPM-632Wを使用しました.
電源部の回路図を図18に示します.