Next: 4 製作 Up: 6CK4を使った各種出力段の比較実験 Previous: 2 設計

3 シミュレーション

3.1 電圧増幅・位相反転段(2002/12/31)

電圧増幅・位相反転段のリストを以下に示します．実験に使用する定電流ダイオードの電流値が 1.07 mA なので，シミュレーションの定電流値もそれに合わせています．

3.1.0.1 `volamp.cir`

    1 5751-6CK4 voltage amplifier
    2 .INCLUDE 5751.lib
    3 XV1a 1 2 3 5751
    4 XV1b 4 5 3 5751
    5 Ik1 3 0 1.07mA
    6 Rg1 2 0 100k
    7 Rg2 5 0 100
    8 Rp1 1 99 270k
    9 Rp2 4 99 270k
   10 Vbb 99 0 240
   11 Cc1 1 6 0.22u
   12 Cc2 4 7 0.22u
   13 Rg3 6 0 270k
   14 Rg4 7 0 270k
   15 .NODESET V(3)=1V
   16 Vin 2 0 DC 0V AC 1V SIN(0 1.606648V 1kHz)
   17 *Vin 2 0 DC 0V AC 1V PWL(0 0V 0.25m 1.606648V 0.75m -1.606648V 1.25m 1.606648V 1.75m -1.606648V 2m 0)
   18 
   19 .control
   20 set width=120
   21 op
   22 print v(1) v(4) v(3) v(1,3) v(4,3)
   23 ac dec 1 1k 1k
   24 print abs(v(6)) abs(v(7))
   25 print db(v(6)) db(v(7))
   26 tran 0.005m 2m 0 0.002m
   27 *plot v(2) v(3) v(2,3) v(5,3)
   28 *plot v(1) v(4)
   29 print v(2) v(3) v(2,3) v(5,3) v(1) v(4)
   30 linearize v(6)
   31 fourier 1kHz v(6)
   32 .endc
   33 .END

3.1.0.2 `5751.lib`

    1 *
    2 * GENERIC: 5751
    3 *
    4 .SUBCKT 5751 A G K
    5 BGG   GG   0 V=V(G,K)+0.56416
    6 BEP   EP   0 V=URAMP(V(A,K))+1e-10
    7 BSTM  STM  0 V=URAMP(V(GG)+V(EP)/60.205)+1e-10
    8 BM1   M1   0 V=(0.0047389751681754*(URAMP(V(EP)-1e-10)+1e-10))^-0.59881207236704
    9 BM2   M2   0 V=(0.71469*V(STM))^2.09881207236704
   10 BM    M    0 V=V(M1)*V(M2)
   11 BSTP  STP  0 V=URAMP(V(GG)+V(EP)/84.2393205445718)+1e-10
   12 BP    P    0 V=1.73303239386834*V(STP)^1.5
   13 BIK   IK   0 V=U(V(GG))*V(P)+(1-U(V(GG)))*V(M)
   14 BLIM  LI   0 V=0.88*V(EP)^1.5
   15 BEG   EG   0 V=URAMP(V(G,K))+1e-10
   16 BIG   IG   0 V=0.88*(V(EG)/(V(EP)+V(EG))*1.2+0.4)*V(EG)^1.5
   17 BIP   IP   0 V=(V(IK,IG)-URAMP(V(IK,IG)-V(LI)))
   18 BIGK  G    K I=0.00076878*V(IG)
   19 BIAK   A    K I=0.00076878*V(IP)
   20 * CAPS
   21 CAK   A    K 4.6e-13
   22 CGK   G    K 1.4e-12
   23 CGA   G    A 1.4e-12
   24 .ENDS

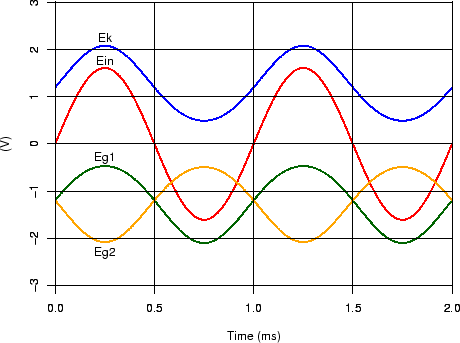
対アースプレート電圧は 95.6 V，カソード電圧(バイアス)は 1.20 V，ゲインは25.1倍(28 dB)となります． 80 V_pp 出力時の歪率は0.263%です．

図19に入力電圧，カソード電圧，グリッド電圧の波形を，図20に対アースプレート電圧の波形を示します．

**図 19:** 5751の入力電圧，カソード電圧，グリッド電圧(シミュレーション)
$\includegraphics{figs/5751simin.ps}$

**図 20:** 5751の対アースプレート電圧(シミュレーション)
$\includegraphics{figs/5751simout.ps}$

3.2 A級シングル出力段(2003/1/25)

A級シングル出力段のリストを以下に示します．

3.2.0.1 `6CK4se.cir`

    1 6CK4 single power amplifier
    2 .INCLUDE 6CK4.lib
    3 .INCLUDE 5751.lib
    4 .INCLUDE OPT2k5.inc
    5 
    6 XV1a 4 1 3 5751
    7 XV1b 5 2 3 5751
    8 R1 1 0 100k
    9 R2 2 0 100
   10 R3 4 6 270k
   11 R4 5 6 270k
   12 Ik1 3 0 1.07mA
   13 C1 4 11 0.22u
   14 C2 5 21 0.22u
   15 R5 11 14 270k
   16 R6 21 24 270k
   17 VC1 14 0 -27.691
   18 VC2 24 0 -27.691
   19 XV2 12 11 13 6CK4
   20 R7 13 0 1
   21 XOPT 12 30 40 0 OPT2k5
   22 *RL 40 0 8.18
   23 RL 40 0 10.7
   24 *RL 40 0 16.3
   25 
   26 VBB 30 0 255.950476
   27 R9 30 6 15k
   28 C5 6 0 22u
   29 
   30 * No NFB
   31 VI 1 0 DC 0V AC 1V SIN(0 1.112V 1kHz)
   32 *VI 1 0 DC 0V AC 1V PWL(0 0V 0.25m 1.112V 0.75m -1.112V 1.25m 1.112V 1.75m -1.112V 2m 0)
   33 
   34 * NFB 6dB
   35 *RNFB 40 2 560
   36 *VI 1 0 DC 0V AC 1V SIN(0 2.5V 1kHz)
   37 
   38 .NODESET V(6)=240 V(3)=1.1
   39 
   40 .control
   41 set width=120
   42 op
   43 print v(6) v(3) v(4) v(5) v(12,13) v(11,13) v(13)
   44 ac dec 1 1k 1k
   45 print abs(v(40))
   46 *tran 0.01m 2m 0 0.005m
   47 *plot v(11,13)
   48 *plot v(12,13)
   49 *plot v(13)
   50 *plot v(40)
   51 *print v(11,13) v(12,13) v(13) v(40)
   52 *linearize v(12) v(13) v(40)
   53 *fourier 1kHz v(12) v(40)
   54 *print sqrt(mean((v(12)-mean(v(12)))^2))
   55 *print mean((v(12)-mean(v(12)))^2) / 2524
   56 *print mean((v(40)-mean(v(40)))^2) / 8.18
   57 *print mean((v(12)-mean(v(12)))^2) / 3204
   58 *print mean((v(40)-mean(v(40)))^2) / 10.7
   59 *print mean((v(12)-mean(v(12)))^2) / 4591
   60 *print mean((v(40)-mean(v(40)))^2) / 16.3
   61 *print mean(v(12)) mean(v(13))
   62 *print v(12) v(13)
   63 *tran 0.020m 50m 0 0.020m
   64 *print v(12,13)
   65 .endc
   66 .END

3.2.0.2 `6CK4.lib`

    1 *
    2 * GENERIC: 6CK4
    3 *
    4 .SUBCKT 6CK4 A G K
    5 BGG   GG   0 V=V(G,K)+1.3222
    6 BEP   EP   0 V=URAMP(V(A,K))+1e-10
    7 BSTM  STM  0 V=URAMP(V(GG)+V(EP)/6.0997)+1e-10
    8 BM1   M1   0 V=(0.0556199485220584*(URAMP(V(EP)-1e-10)+1e-10))^-0.77019909646076
    9 BM2   M2   0 V=(0.660735*V(STM))^2.27019909646076
   10 BM    M    0 V=V(M1)*V(M2)
   11 BSTP  STP  0 V=URAMP(V(GG)+V(EP)/9.23168895245446)+1e-10
   12 BP    P    0 V=1.67095052790759*V(STP)^1.5
   13 BIK   IK   0 V=U(V(GG))*V(P)+(1-U(V(GG)))*V(M)
   14 BLIM  LI   0 V=0.88*V(EP)^1.5
   15 BEG   EG   0 V=URAMP(V(G,K))+1e-10
   16 BIG   IG   0 V=0.88*(V(EG)/(V(EP)+V(EG))*1.2+0.4)*V(EG)^1.5
   17 BIP   IP   0 V=(V(IK,IG)-URAMP(V(IK,IG)-V(LI)))
   18 BIGK  G    K I=0.00185*V(IG)
   19 BIAK   A    K I=0.00185*V(IP)
   20 * CAPS
   21 CAK   A    K 1.8e-12
   22 CGK   G    K 8e-12
   23 CGA   G    A 6.5e-12
   24 .ENDS

3.2.0.3 `OPT2k5.inc`

    1 *
    2 *   OPT 2k5
    3 *
    4 .SUBCKT OPT2k5 P B S1 S0
    5 * Primary inductance (2500ohm 12.12H)
    6 L1 P 1 12.12
    7 * Iron loss
    8 RI P 1 291k
    9 * Primary DC resistance
   10 R1 1 B 146.8
   11 * Primary stray capacitance
   12 CP P B 393.3p
   13 * Secondary inductance (8ohm)
   14 L2 S1 2 0.04338939
   15 * Secondary DC resistance
   16 R2 2 S0 0.66
   17 * Secondary stray capacitance
   18 CS S1 S0 2840p
   19 * coupling factor
   20 K L1 L2 0.99959
   21 .ENDS

各部の波形を図21から図25に示します．目盛は，第5節のオシロの画面とほぼ等しくなるようにしてあります．図24のクリップですが，グリッド電圧は頭が平らに切れていますが，プレート電圧，プレート電流で見ると斜めになっています．シングル用のOPTは，1次インダクタンスが少ないので，ロードラインが楕円になり，このようなクリップの波形が生じます．プレート損失の波形(図25)は，かなり複雑な形状をしています．ロードラインのグラフ(図4)より，プラスの入力が加わっていくと， E_g = - 17 V あたりでロードラインが最大プレート損失(点線)に最も近づき，その後離れていくことから，一周期につき2つの山ができることがわかります．マイナスの入力が加わると，ロードラインと最大プレート損失の曲線は離れていくので，単純な谷ができます．図25には無信号時のプレート損失 P_d0 = 10.42 W と最大出力時のプレート損失 P_dsig = 7.37 W も記入しました．得られる信号出力は，最大出力時のプレート入力からプレート損失を引いたものになりますが，シングルの場合は，最大出力時のプレート入力は無信号時のプレート損失とほとんど変わらないので，P_d0 と P_dsig の差が，ほぼ最大出力になります．

**図 21:** 6CK4シングル出力段のグリッド電圧，OPT 2次電圧(シミュレーション 3.2k)
$\includegraphics{figs/6CK4simse3k2EgEo.ps}$

**図 22:** 6CK4シングル出力段のプレート電圧，プレート電流(シミュレーション 3.2k)
$\includegraphics{figs/6CK4simse3k2EpIp.ps}$

**図 23:** 6CK4シングル出力段のロードラインと伝達特性(シミュレーション 3.2k)
$\includegraphics{figs/6CK4simse3k2lltc.ps}$

**図 24:** 6CK4シングル出力段のクリップ時のグリッド電圧，OPT 2次電圧，プレート電圧，プレート電流(シミュレーション 3.2k)
$\includegraphics{figs/6CK4simse3k2clip.ps}$

**図 25:** 6CK4シングル出力段のプレート損失(シミュレーション 3.2k)
$\includegraphics{figs/6CK4simse3k2Pd.ps}$

3.3 A級プッシュプル出力段(2003/1/26)

A級プッシュプル出力段のリストを以下に示します．

3.3.0.1 `6CK4pp.cir`

    1 6CK4 push pull amplifier
    2 .INCLUDE 6CK4.lib
    3 .INCLUDE 5751.lib
    4 .INCLUDE F2021.inc
    5 
    6 XV1a 4 1 3 5751
    7 XV1b 5 2 3 5751
    8 R1 1 0 100k
    9 R2 2 0 330
   10 R3 4 6 270k
   11 R4 5 6 270k
   12 Ik1 3 0 1.07mA
   13 C1 4 11 0.22u
   14 C2 5 21 0.22u
   15 R5 11 14 270k
   16 R6 21 24 270k
   17 VC1 14 0 -27.691
   18 VC2 24 0 -27.691
   19 XV2 12 11 13 6CK4
   20 R7 13 0 1
   21 XV3 22 21 23 6CK4
   22 R8 23 0 1
   23 XOPT 12 30 30 22 40 0 F2021
   24 *RL 40 0 8.18
   25 RL 40 0 10.7
   26 *RL 40 0 16.3
   27 
   28 VBB 30 0 252.941902
   29 R9 30 6 15k
   30 C5 6 0 22u
   31 
   32 * No NFB
   33 VI 1 0 DC 0V AC 1V SIN(0 1.106V 1kHz)
   34 *VI 1 0 DC 0V AC 1V PWL(0 0V 0.25m 1.106V 0.75m -1.106V 1.25m 1.106V 1.75m -1.106V 2m 0)
   35 
   36 * NFB 6dB
   37 *RNFB 40 2 560
   38 *VI 1 0 DC 0V AC 1V SIN(0 2.5V 1kHz)
   39 
   40 .NODESET V(6)=240 V(3)=1.1
   41 
   42 .control
   43 op
   44 set width=120
   45 print v(6) v(3) v(4) v(5)
   46 print v(12,13) v(11,13) v(13)
   47 print v(22,23) v(21,23) v(23)
   48 ac dec 1 1k 1k
   49 print abs(v(40))
   50 *tran 0.01m 2m 0 0.005m
   51 *plot v(11,13)
   52 *plot v(12,13)
   53 *plot v(13)
   54 *plot v(22,23)
   55 *plot v(23)
   56 *print v(11,13) v(12,13) v(13) v(40) v(23)
   57 *linearize v(12) v(13) v(40)
   58 *fourier 1kHz v(40)
   59 *print sqrt(mean((v(12)-mean(v(12)))^2))
   60 *print mean((v(12)-mean(v(12)))^2) / 4972 * 4
   61 *print mean((v(40)-mean(v(40)))^2) / 8.18
   62 *print mean((v(12)-mean(v(12)))^2) / 6359 * 4
   63 *print mean((v(40)-mean(v(40)))^2) / 10.7
   64 *print mean((v(12)-mean(v(12)))^2) / 9392 * 4
   65 *print mean((v(40)-mean(v(40)))^2) / 16.3
   66 *print mean(v(12)) mean(v(13))
   67 *print v(12) v(13)
   68 .endc
   69 .END

3.3.0.2 `F2021.inc`

    1 *
    2 *   TAMURA OPT F2021
    3 *
    4 .SUBCKT F2021 P1 B1 B2 P2 S8 S0
    5 * 1次インダクタンス(p-p 5kohm 150H)
    6 L11 P1 12 30.92H
    7 L12 13 P2 30.92H
    8 * 1次巻線抵抗
    9 R11 12 B1 64.7
   10 R12 B2 13 73.5
   11 * 1次巻線浮遊容量
   12 C11 P1 B1 1126p
   13 C12 P2 B2 1126p
   14 * 鉄損
   15 RI1 P1 12 158.4k
   16 RI2 P2 13 158.4k
   17 * 2次インダクタンス(8ohm)
   18 L2 S8 16 0.208279
   19 * 2次巻線抵抗
   20 R13 S0 16 0.25
   21 * 結合係数
   22 K1 L11 L2  0.9999714
   23 K2 L12 L2  0.9999714
   24 K3 L11 L12 0.99994
   25 .ENDS

波形を図26から図31に示します．プッシュプル用のOPTは1次インダクタンスが大きいので，ロードラインも伝達特性もそれほど膨らんでいません．図29の左側は，合成プレート電流( I_psyn = I_p1 - I_p2)と， 2管の総プレート電流( I_ptotal = I_p1 + I_p2)の波形です．真空管1本ずつのプレート電流の波形は，かなり歪んでいますが， 2本のプレート電流を合成すると，きちんとした波形に戻ります．総プレート電流には，入力信号の2倍の周波数の成分が含まれます．図29の右側は，各球のロードライン(水色)と合成ロードライン(青色)です．おもしろいのはクリップ時の波形(図30で，片側のグリッド電圧が正になると負荷インピーダンスが急激に小さくなり，電圧増幅段のACバランスが崩れ，もう一方のグリッド電圧はさらに低くなります．その結果，クリップ時のプレート電流に谷ができているようです．プレート損失の波形(図31)の振幅は，シングルの時よりも小さくなっています．ロードラインの形状が定プレート損失曲線(双曲線)に近いため，信号を加えてもプレート損失があまり変化しません．また，最大出力時にはプレート入力が増えているため，出力を取り出してもプレート損失( P_dsig = 9.81 W)がそれほど下がっていません．

**図 26:** 6CK4プッシュプル出力段のグリッド電圧，OPT 2次電圧(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simpp6k4EgEo.ps}$

**図 27:** 6CK4プッシュプル出力段のプレート電圧，プレート電流(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simpp6k4EpIp.ps}$

**図 28:** 6CK4プッシュプル出力段のロードラインと伝達特性(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simpp6k4lltc.ps}$

**図 29:** 6CK4プッシュプル出力段の合成プレート電流波形と合成ロードライン(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simpp6k4syn.ps}$

**図 30:** 6CK4プッシュプル出力段のクリップ時のグリッド電圧，OPT 2次電圧，プレート電圧，プレート電流(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simpp6k4clip.ps}$

**図 31:** 6CK4プッシュプル出力段のプレート損失(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simpp6k4Pd.ps}$

図32は， Z_pp = 6.4 kΩ と Z_pp = 9.4 kΩ の場合の出力対歪率特性です．歪率には，位相反転段の歪みも含まれています． THDはクリップまで出力に比例して増加します．クリップしたあとは，一旦THDが減り，その後再び増加します．このとき，3次歪みが急激に減る一方，5次歪みが急増しています．さらにクリップが激しくなると，再び3次歪みが優勢になります． 1 W 出力時の歪率は，ほとんど同じですが，それ以上の出力では， Z_pp = 9.4 kΩ の方が歪みが大きくなっています．

**図 32:** 6CK4プッシュプル出力段の出力対歪率特性(シミュレーション左6.4k 右9.4k)
$\includegraphics{figs/6CK4simppPoK.ps}$

3.4 差動出力段(2003/1/26)

差動出力段のリストを以下に示します．

3.4.0.1 `6CK4diff.cir`

    1 6CK4 differential power amplifier
    2 .INCLUDE 6CK4.lib
    3 .INCLUDE 5751.lib
    4 .INCLUDE F2021.inc
    5 
    6 XV1a 4 1 3 5751
    7 XV1b 5 2 3 5751
    8 R1 1 0 100k
    9 R2 2 0 330
   10 R3 4 6 270k
   11 R4 5 6 270k
   12 Ik1 3 0 1.07mA
   13 C1 4 11 0.22u
   14 C2 5 21 0.22u
   15 R5 11 0 270k
   16 R6 21 0 270k
   17 XV2 12 11 13 6CK4
   18 R7 13 31 10
   19 XV3 22 21 23 6CK4
   20 R8 23 31 10
   21 Ik2 31 0 83.34mA
   22 XOPT 12 30 30 22 40 0 F2021
   23 *RL 40 0 8.18
   24 *RL 40 0 10.7
   25 RL 40 0 16.3
   26 
   27 VBB 30 0 280.7
   28 R9 30 6 39k
   29 C5 6 0 22u
   30 
   31 * No NFB
   32 VI 1 0 DC 0V AC 1V SIN(0 1.265V 1kHz)
   33 *VI 1 0 DC 0V AC 1V PWL(0 0V 0.25m 1.265V 0.75m -1.265V 1.25m 1.265V 1.75m -1.265V 2m 0)
   34 
   35 * NFB 6dB
   36 *RNFB 40 2 560
   37 *VI 1 0 DC 0V AC 1V SIN(0 2.5V 1kHz)
   38 
   39 .NODESET V(6)=240 V(3)=1.1V V(31)=27.7V
   40 
   41 .control
   42 set width=120
   43 op
   44 print v(6) v(3) v(4) v(5)
   45 print v(12,13) v(11,13) v(13)
   46 print v(22,23) v(21,23) v(23)
   47 ac dec 1 1k 1k
   48 print abs(v(40))
   49 *ac dec 30 1 1Meg
   50 *plot db(v(40))
   51 *tran 0.01m 2m 0 0.005m
   52 *plot v(11,13)
   53 *plot v(12,13)
   54 *plot v(13)
   55 *print v(11,13) v(12,13) v(13,31) v(40) v(13) v(23,31)
   56 *linearize v(12) v(13) v(40)
   57 *fourier 1kHz v(40)
   58 *print sqrt(mean((v(12)-mean(v(12)))^2))
   59 *print mean((v(12)-mean(v(12)))^2) / 4972 * 4
   60 *print mean((v(40)-mean(v(40)))^2) / 8.18
   61 *print mean((v(12)-mean(v(12)))^2) / 6359 * 4
   62 *print mean((v(40)-mean(v(40)))^2) / 10.7
   63 *print mean((v(12)-mean(v(12)))^2) / 9392 * 4
   64 *print mean((v(40)-mean(v(40)))^2) / 16.3
   65 *print mean(v(12)) mean(v(13))
   66 *print v(12) v(13)
   67 .endc
   68 .END

波形を図33から図38に示します．出力管の非直線性から生じる2球のプレート電流のアンバランスをバランスさせるため，カソードの電圧が変動し，その結果，グリッド電圧は負の方向に引き延ばされます．プレート電圧およびプレート電流は上下対称の波形になります．図36の左側の総プレート電流 I_ptotal は，定電流回路が入っているため一定になっています．図36の右側の合成ロードライン(青色)は，カソード電圧を加えた対アースのプレート電圧で示しています．出力トランスの起点すなわち E_bb は，交流的にはアースと等価であり，合成ロードラインは，アース基準で直線になります．図38のプレート損失の波形は，シングルの場合と似ています．

**図 33:** 6CK4差動出力段のグリッド電圧，カソード電圧(シミュレーション 9.4k)
$\includegraphics{figs/6CK4simdiff9k4EgEo.ps}$

**図 34:** 6CK4差動出力段のプレート電圧，プレート電流(シミュレーション 9.4k)
$\includegraphics{figs/6CK4simdiff9k4EpIp.ps}$

**図 35:** 6CK4差動出力段のロードラインと伝達特性(シミュレーション 9.4k)
$\includegraphics{figs/6CK4simdiff9k4lltc.ps}$

**図 36:** 6CK4プッシュプル出力段の合成プレート電流波形と合成ロードライン(シミュレーション 6.4k)
$\includegraphics{figs/6CK4simdiff9k4syn.ps}$

**図 37:** 6CK4差動出力段のクリップ時のグリッド電圧，カソード電圧，プレート電圧，プレート電流(シミュレーション 9.4k)
$\includegraphics{figs/6CK4simdiff9k4clip.ps}$

**図 38:** 6CK4差動出力段のプレート損失(シミュレーション 9.4k)
$\includegraphics{figs/6CK4simdiff9k4Pd.ps}$

図39は， Z_pp = 6.4 kΩ と Z_pp = 9.4 kΩ の場合の出力対歪率特性です．出力が増加する以上にTHDが増えています． Z_pp = 6.4 kΩ の場合はクリップせずにカットオフが起こりますが， A級プッシュプルの場合とは異なり，入力を大きくしても歪みが減ることはありません． Z_pp = 9.4 kΩ の場合は約 6.5 W でクリップしますが，クリップしたあとは，急激に歪みが増加します．

**図 39:** 6CK4差動出力段の出力対歪率特性(シミュレーション左6.4k 右9.4k)
$\includegraphics{figs/6CK4simdiffPoK.ps}$

プッシュプルと差動出力段のTHDを同時にプロットしたのが，図40です． Z_pp = 6.4 kΩ の場合，3.8 W までは差動出力段の方が歪率が低くなっています． Z_pp = 9.4 kΩ の場合，差動出力段の歪率は，プッシュプルと比べるとかなり低くなっています．

**図 40:** 6CK4プッシュプル出力段と差動出力段の出力対歪率特性の比較(シミュレーション左6.4k 右9.4k)
$\includegraphics{figs/6CK4simPoKcmp.ps}$

Next: 4 製作 Up: 6CK4を使った各種出力段の比較実験 Previous: 2 設計

Ayumi Nakabayashi
平成19年7月7日