

Next: 10 位相補償
Up: オーディオのための交流理論入門
Previous: 8 能動素子の等価回路とポール
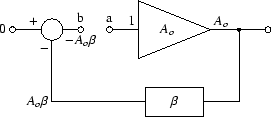
負帰還とは,図97のように,
アンプの出力を  倍(通常は
倍(通常は

 1)し,
それを入力から差し引くものです.
1)し,
それを入力から差し引くものです.
図 97:
負帰還
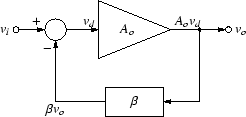 |
実質的なアンプの入力信号 vd は,
vd = vi - 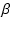 vo vo
|
(272) |
で,これが Ao 倍されたものが出力 vo となります.
これから vd を消去すれば,
負帰還回路の入出力の関係,すなわち伝達関数が求められます.
| vo |
= |
Ao(vi - 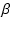 vo) vo) |
|
(1 + Ao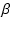 )vo )vo |
= |
Aovi |
|
| vo |
= |
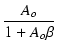 vi vi |
(274) |
| Af(s) |
= |
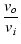 = = 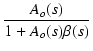 |
(275) |
負帰還をかけた後のゲイン Af(s) は,クローズドループゲイン(closed loop gain)といいます.
負帰還をかける前のゲイン Ao(s) は,オープンループゲイン(open loop gain)といいます.
帰還前と帰還後のゲインの比率は帰還量(feedback) F で,
F = 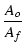 = 1 + Ao = 1 + Ao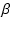
|
(276) |
です.
一般には帰還回路( 回路ともいう)は受動素子,
特に抵抗を使って構成する場合が多く,
回路ともいう)は受動素子,
特に抵抗を使って構成する場合が多く,
 に周波数特性がない場合が多いのですが,
ここでは
に周波数特性がない場合が多いのですが,
ここでは  (s) として,周波数特性がある場合も考えます.
(s) として,周波数特性がある場合も考えます.
また,この図では,アンプは出力から入力に信号を伝えない,
また  回路は左側から右側に信号を伝えないことが仮定されていますが,
そのような仮定が成り立たない場合には,
漸近利得という概念を使って解析します.
オーディオにおいては,通常は上述の仮定が成り立っていますので,
漸近利得による解析は,ここでは扱いません.
興味のある方は,[2], [1]などを参照してください.
回路は左側から右側に信号を伝えないことが仮定されていますが,
そのような仮定が成り立たない場合には,
漸近利得という概念を使って解析します.
オーディオにおいては,通常は上述の仮定が成り立っていますので,
漸近利得による解析は,ここでは扱いません.
興味のある方は,[2], [1]などを参照してください.
式(275)より,Ao が十分大きければ,
が十分大きければ,
と近似できますので,
アンプのゲインや周波数特性は,帰還後の特性にほとんど影響を与えず,
 回路の特性によって決まることが分かります.
回路の特性によって決まることが分かります.
ここで,図98のように,アンプの入力のところで回路を切ります.
図 98:
ループゲイン
 |
入力に信号を与えず,点aに単位信号(たとえば 1V)を与えます.
このとき,点bに現れた信号の負の値をループゲイン(loop gain)といい,
T(s) で表します.
図より,
T(s) = Ao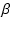
|
(278) |
となることは明らかです.
ループゲインは,負帰還回路の安定性を調べるときに大変重要で,
ループゲインが -1 (絶対値が1倍かつ位相が 180o 進むか遅れる)になると,
点bには点aと同じ信号が現れるので,
ループを閉じれば入力 vi がなくても出力が生じる,つまり発振してしまいます.
点bからみた点aの信号の大きさ,すなわち点aと点bの信号の差は,還送差といい,
1 - (- Ao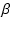 ) = 1 + Ao ) = 1 + Ao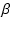 = F = F
|
(279) |
となり,先ほど示した帰還量と同じです.
ループゲインの定義でみたように,
アンプの入力には1単位の信号を加えています.
その結果,点bには - Ao の信号が生じており,
それを打ち消して,さらに点aに1単位の信号が生じるような入力を加えてやれば,
アンプの出力は帰還前の出力と同じになります.
そのときの入力は,
F = 1 + Ao
の信号が生じており,
それを打ち消して,さらに点aに1単位の信号が生じるような入力を加えてやれば,
アンプの出力は帰還前の出力と同じになります.
そのときの入力は,
F = 1 + Ao で,
それだけアンプの入力感度が低くなっているわけで,
還送差は帰還量と一致することになります.
で,
それだけアンプの入力感度が低くなっているわけで,
還送差は帰還量と一致することになります.
ループゲインは,負帰還のループのどこで切断しても求められます.
一般には,切断した影響が少なくなるよう,
(b点の)出力インピーダンスが低く,(a点の)入力インピーダンスが高くなる点を選びます.
パワーアンプであれば,
アンプの出力と  回路の入力の間で切断するのがよいでしょう.
DCアンプなど,負帰還がないと動作点が定まらないような場合は,
インダクタなどを入れて,直流には負帰還がかかり,
交流信号には負帰還がかからないような措置を施す必要があります.
切断する適切な箇所がアンプ内にある場合もあります.
回路の入力の間で切断するのがよいでしょう.
DCアンプなど,負帰還がないと動作点が定まらないような場合は,
インダクタなどを入れて,直流には負帰還がかかり,
交流信号には負帰還がかからないような措置を施す必要があります.
切断する適切な箇所がアンプ内にある場合もあります.
今まで出てきた用語と式をまとめると,次のようになります.
| オープンループゲイン |
Ao |
| 帰還率 |
 |
| ループゲイン |
T = Ao |
| クローズドループゲイン |
Af = 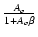 = = 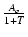 = = 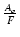 |
| 帰還量,還送差 |
F = 1 + Ao = 1 + T = 1 + T |
負帰還の安定性を検討するために,
ナイキスト線図やニコルス線図などを使うこともありますが,
一番多く使われるのが,ボーデ線図(Bode chart)です.
ボーデ線図は,横軸に周波数をとり,
縦軸には,ゲインをデシベルで表したものと位相をとったものです(図99).
図 99:
ボーデ線図
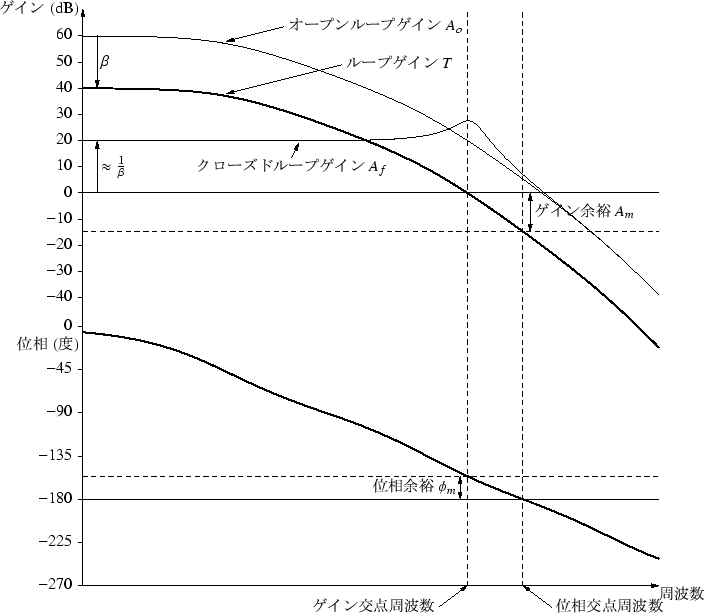 |
負帰還の安定性を検討するには,ループゲインのボーデ線図を描きます.
ボーデ線図上で,ループゲインが 0dB になるまでに,位相が
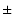 180o 以下であれば,安定です.
また別の言い方をすれば,位相が
180o 以下であれば,安定です.
また別の言い方をすれば,位相が
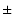 180o に達するまでに,
ループゲインが 0dB 以下になっていれば,安定です.
ただし,安定といっても発振しないというだけで,
周波数特性にピークができることはあります.
180o に達するまでに,
ループゲインが 0dB 以下になっていれば,安定です.
ただし,安定といっても発振しないというだけで,
周波数特性にピークができることはあります.
負帰還をかけたときにどの程度安定かを判断するために,
位相余裕(phase margin)やゲイン余裕(gain margin)というものが使われます.
位相余裕は,ループゲインが 0dB となったときの,ループゲインの位相と
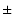 180o との差です.
ゲイン余裕は,ループゲインの位相が
180o との差です.
ゲイン余裕は,ループゲインの位相が
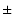 180o になったときの,
ループゲインと 0dB との差です.
180o になったときの,
ループゲインと 0dB との差です.
アンプのオープンループゲインとして,
低域のゲインが A0 で,ポールが p のローパス特性を考えます.
伝達関数は,
Ao(s) = 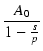
|
(280) |
です.
周波数特性がフラットな  回路で負帰還をかけると,
クローズドループ特性は,
回路で負帰還をかけると,
クローズドループ特性は,
となります.
この式の第1項は,s を含まない部分であり,
帰還後の低域のゲインが
Af(0) = A0/(1 + A0 ) となることがわかります.
この式の第2項は,1次のローパス特性であり,そのポール p' は,
) となることがわかります.
この式の第2項は,1次のローパス特性であり,そのポール p' は,
p' = (1 + A0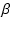 )p = F0p )p = F0p
|
(282) |
です.
ここで,F0 は低域の帰還量で
F0 = 1 + A0 です.
つまり,負帰還により,
高域のポールが,低域の帰還量だけ高いほうに移動することがわかります.
です.
つまり,負帰還により,
高域のポールが,低域の帰還量だけ高いほうに移動することがわかります.
低域のゲインが100で,10kHz にポールを持つ回路に 20dB の負帰還をかけた場合の特性を求めます.
| A0 |
= |
100 |
|
| p |
= |
-2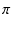 . 10 x 103 . 10 x 103 |
|
| Ao(s) |
= |
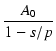 = = 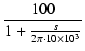 |
|
| F |
= |
10 |
|
これより,
となります.
Rの関数は,次のようになります.
function ()
{
A0 <- 100 # 低域のオープンループゲイン
p <- -2 * pi * 10e3 # ポール(10kHz)
F <- 10 # 帰還量
b <- (F - 1) / A0 # 帰還率
f <- dec(1e3, 1e6, 30)
s <- 2 * pi * f * (0+1i)
Ao <- A0 / (1 - s/p) # 各周波数のオープンループゲイン
Af <- Ao / (1 + Ao * b) # クローズドループゲイン
y <- cbind(Ao, Af)
x <- list(f=f, A=y, arg=Arg(y)*180/pi)
par(mfrow=c(2, 1))
col <- c("red", "blue")
bode.gain(x, lty=1, col=col, ylim=c(0, 45), yaxs="i")
abline(v=log10(-p/2/pi), col="red") # 帰還前のカットオフ周波数
abline(v=log10(-p/2/pi*F), col="blue") # 帰還後のカットオフ周波数
bode.phase(x, lty=1, col=col, ylim=c(-90, 0), yaxs="i")
}
図 100:
時定数が1段の回路に負帰還をかけた特性
|
|
前節のように,時定数が1段しかない場合,位相は最大でも 90o しか変化せず,
負帰還をかけた後の特性もポールが一つしかなく,ピークは生じません.
ところで,負帰還アンプの各部の電圧をベクトル図で表してみましょう.
アンプ自体の実質的な入力 vd を基準にすると,図101のようになります.
図 101:
負帰還のベクトル図
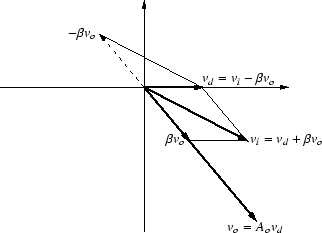 |
負帰還をかけない場合のアンプ自体の位相の遅れは,x軸と vo のなす角です.
負帰還をかけた場合,位相の遅れは,vi と vo のなす角となり,
帰還前よりも小さくなります.
vd を1とすれば vo = Ao で,
vi は
1 + Ao となることも,この図からわかります.
となることも,この図からわかります.
ループゲインの定義より,ループゲインは vd = 1 を与えたときの,
 vo =
vo =  Ao になります.
ゲイン交点周波数では,ループゲインの絶対値が1になりますが,
これは
Ao になります.
ゲイン交点周波数では,ループゲインの絶対値が1になりますが,
これは  Ao の絶対値が1になることを意味しています.
また
Ao の絶対値が1になることを意味しています.
また  Ao とx軸の負方向とでなす角が位相余裕
Ao とx軸の負方向とでなす角が位相余裕 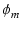 になります.
位相余裕が 60o のときのベクトル図を図102に示します.
になります.
位相余裕が 60o のときのベクトル図を図102に示します.
図 102:
位相余裕が60度の場合
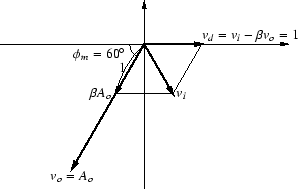 |
位相余裕が 60o の場合,vi の絶対値も1になります.
すなわち同じ vo = Ao という出力に対して,
帰還前の入力 vd も帰還後の入力 vi も絶対値が等しいので,
ゲインは帰還前と帰還後とで変わりません.
ただし位相の遅れは帰還後のほうが小さくなります.
位相余裕が 45o の場合を図103に示します.
図 103:
位相余裕が45度の場合
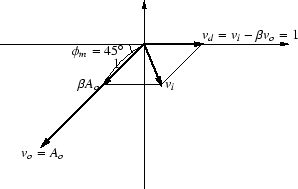 |
この場合,帰還後の入力 vi の絶対値が1より小さくなっているので,
ゲインは帰還前よりも大きくなっています.
このように,位相余裕が 60o よりも小さくなると,
ゲイン交点周波数では,帰還後のほうがゲインが大きくなります.
ゲインが帰還前よりも大きくなっているので,
正帰還になっているともいえます.
位相余裕が 90o の場合を図104に示します.
図 104:
位相余裕が90度の場合
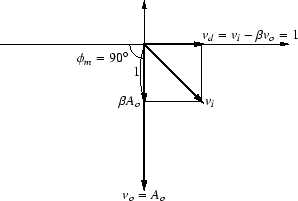 |
この場合,帰還後の入力 vi の絶対値は
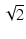
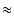 1.41 で,
ゲインは帰還前の
1/1.41
1.41 で,
ゲインは帰還前の
1/1.41 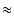 0.7 倍となります.
0.7 倍となります.
ここまではゲイン交点における負帰還アンプの振る舞いを調べてきましたが,
位相余裕を 60o 以上とっておけば,
それほど大きなピークが生じないであろうことがわかります.
ゲイン交点周波数以外でどのような特性になるかを一般的に論じるのは困難なので,
いくつか仮定を置くことにします.
位相余裕が 90o より小さくなるということは,
位相の遅れが 90o 以上になるということで,
少なくとも2つのポールが存在しなくてはなりません.
2つのポールが近くにあるという状況は一般的に表せないので,
2つのポールが離れていると仮定します.
また,浅い負帰還では負帰還の問題が現れにくいので,
低域のループゲインが非常に大きいと仮定します.
この仮定にもとづいて,一方のポールは積分回路によって生じるとします.
ここでは,ある基準周波数  でゲインの絶対値が1で,
周波数が低くなるにつれて
+6 dB/oct でゲインが上昇し続ける積分回路と,
通常のRCによるローパス特性を組み合わせて,
でゲインの絶対値が1で,
周波数が低くなるにつれて
+6 dB/oct でゲインが上昇し続ける積分回路と,
通常のRCによるローパス特性を組み合わせて,
 においてオープンループゲインの絶対値が1となり,
その時の位相余裕が希望の値になるような回路を考えます.
この回路に
においてオープンループゲインの絶対値が1となり,
その時の位相余裕が希望の値になるような回路を考えます.
この回路に  = 1 の全帰還をかけた場合のゲインを求めます.
全帰還をかけた場合の低域のゲインは1です.
= 1 の全帰還をかけた場合のゲインを求めます.
全帰還をかけた場合の低域のゲインは1です.
積分回路の伝達関数 A1 は,
A1 = 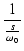
|
(283) |
で,位相は常に 90o 遅れます.
位相余裕が 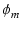 の場合,
第2のポールによる位相の遅れ
の場合,
第2のポールによる位相の遅れ 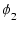 は,
は,
より,
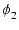 = - 90 + = - 90 + 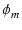
|
(284) |
となります.
第2のポールの伝達関数 A2 を
A2 = A20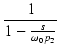
|
(285) |
とおけば,ゲインは,
| A2| = A20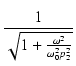
|
(286) |
位相は,
arg A2 = tan-1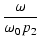
|
(287) |
で,
 =
=  のゲインが1,位相が
のゲインが1,位相が 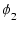 となる A20, p2 を求めればよいことになります.
となる A20, p2 を求めればよいことになります.
| p2 |
= |
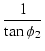 |
(288) |
| A20 |
= |
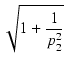 |
(289) |
さまざまな位相余裕について,A20, p2 を求めると,以下のようになります.
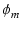 (o) (o) |
p2 |
A20 |
| 90 |
- 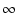 |
1 |
| 60 |
-1.732 |
1.1547 |
| 45 |
-1 |
1.414 |
| 30 |
-0.5774 |
2 |
| 20 |
-0.3640 |
2.9238 |
それぞれの周波数特性は,図105のようになります.
位相余裕が 60o の場合,ゲイン交点周波数ではゲインが1になっていますが,
それより低い周波数ではゲインが1を上回っています.
完全にピークをなくすには,位相余裕を 65o ほど取らねばなりません.
シミュレーションの回路と結果は,図106のようになります.
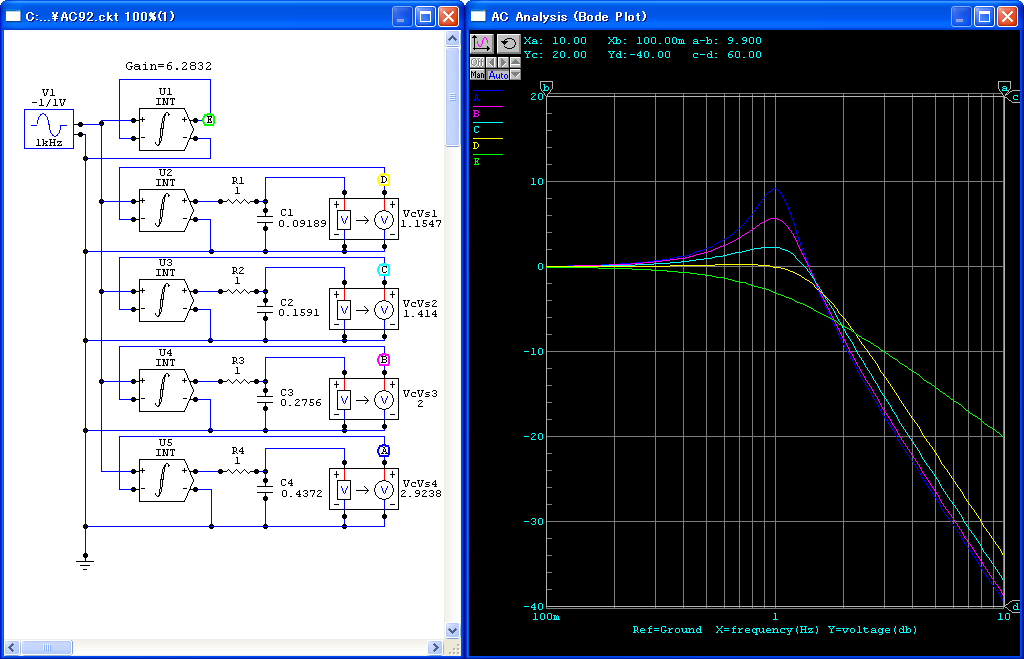
図 106:
位相余裕のシミュレーション
 |
積分器のゲインを6.2832に設定して,1Hz でゲインが1となるようにしています.
積分器の出力インピーダンスは0なので,
その後ろにRCによるローパスフィルタを直接接続し,
さらにゲインを持たせたバッファを接続して出力としています.
負帰還は,積分器が差動入力となっているので,そのマイナス端子に出力を戻しています.
まず,2個の極を持つ伝達関数の特性を調べます.
一般に,このような伝達関数 H(s) は,
H(s) = 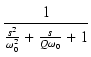
|
(290) |
のように表せます.
 は Q =
は Q = 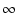 のときに,インパルスを与えると自然に発生する振動の固有周波数です.
Q は
s = j
のときに,インパルスを与えると自然に発生する振動の固有周波数です.
Q は
s = j のときのゲインです.
のときのゲインです.
ゲインは,s に j を代入して絶対値をとることにより求められ,
を代入して絶対値をとることにより求められ,
| H(j )| = )| = 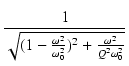
|
(291) |
となります.
Q を変えたときの,ゲインの周波数特性の変化は,
図107のようになります.
Q < 1/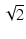 のとき,ゲインの特性にピークは見られません.
Q = 1/
のとき,ゲインの特性にピークは見られません.
Q = 1/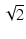 のとき,最大平坦振幅特性が得られ,
これは2次のバタワース特性と呼ばれます.
Q > 1/
のとき,最大平坦振幅特性が得られ,
これは2次のバタワース特性と呼ばれます.
Q > 1/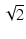 のとき,周波数特性にピークが生じますが,
このピークの周波数
のとき,周波数特性にピークが生じますが,
このピークの周波数 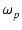 を求めてみます.
式(291)をさらに変形すると,
を求めてみます.
式(291)をさらに変形すると,
となりますので,
ピークを生じる周波数は,
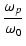 = = 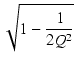
|
(293) |
ピークの大きさ Ap は,
Ap = 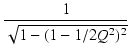 = = 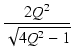
|
(294) |
となります.
ピークの大きさに対する Q の値の例を,以下に示します.
| ピーク(dB) |
Q |
| 0 |
0.707 |
| 0.5 |
0.864 |
| 1 |
0.957 |
| 2 |
1.129 |
| 3 |
1.305 |
| 6 |
1.927 |
| 10 |
3.12 |
| 20 |
9.99 |
またグラフで表すと,図108のようになります.
伝達関数(290)は,Q > 1/2 のとき複素数の極を持ちます.
このとき,
| b |
= |
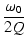 |
(295) |
| a |
= |
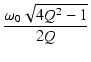 |
(296) |
とおけば,伝達関数を次のように書くことができ,
H(s) = 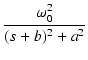
|
(297) |
この関数のインディシャルレスポンス(ステップ応答)は,
H(s)/s をラプラス逆変換6して求めることができます.
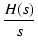 = = ![$\displaystyle {\frac{{\omega_0^2}}{{s[(s+b)^2+a^2]}}}$](img661.png)
|
(298) |
より,これをラプラス逆変換すると
v(t) = 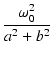 [1 - e-bt(cos at + [1 - e-bt(cos at + 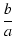 sin at)] sin at)]
|
(299) |
となるので,
v(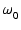 t) = 1 - e- t) = 1 - e-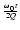  cos cos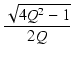 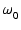 t + t + 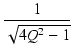 sin sin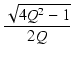 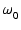 t t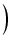
|
(300) |
となります.
最後の瞬時値の関数の変数が  t となっていますが,
t となっていますが,
 と t は常にペアで現われるため,
角周波数で基準化した時間
と t は常にペアで現われるため,
角周波数で基準化した時間  t の関数であると考えてよいためです.
t の関数であると考えてよいためです.
このステップ応答のオーバーシュートの大きさを求めるため,
式(300)が最大になる時刻を求めます.
まず,式(300)を  t について微分すると,
t について微分すると,
v'(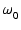 t) t) |
= |
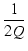 e- e-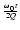  cos cos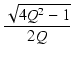 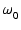 t + t + 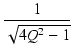 sin sin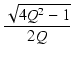 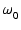 t t |
|
| |
|
- e-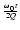  - - 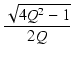 sin sin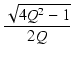 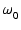 t + t + 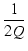 cos cos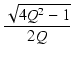 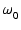 t t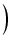 |
|
| |
= |
e-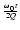  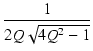 + + 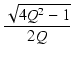  sin sin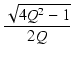 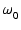 t t |
(301) |
となるので,
t = 0 以降でこれが最初に0となる時刻では,
ですから,
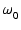 tピーク = tピーク = 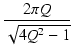
|
(303) |
となります.
これを式(300)に代入すると,ピークの大きさは,
vピーク = 1 + e-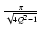
|
(304) |
となります.
したがって,オーバーシュートの大きさは,
vオーバーシュート = e-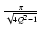
|
(305) |
となります.
Q = 1/2 のとき,伝達関数は,
H(s) = 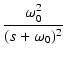
|
(306) |
となり,インディシャルレスポンスは,
v(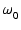 t) = 1 - e- t) = 1 - e-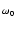 t(1 + t(1 + 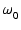 t) t)
|
(307) |
となります.
Q < 1/2 のとき,伝達関数の極は,
となり,
インディシャルレスポンスは,
| v(t) |
= |
1 + 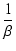 e e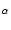 t( t(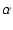 sinh sinh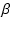 t - t - 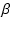 cosh cosh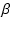 t) t) |
|
| |
= |
1 + e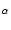 t( t(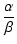 sinh sinh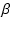 t - cosh t - cosh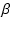 t) t) |
(310) |
ですから,
v(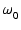 t) = 1 - e- t) = 1 - e-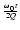  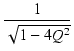 sinh sinh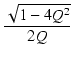 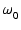 t + cosh t + cosh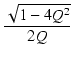 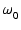 t t
|
(311) |
が得られます.
Q を変えたときのステップ応答のようすは,
図109のようになります.
また,Q とオーバーシュートの関係を図110に示します.
低域のゲインが A0 で,2つの負の実数の極 p1, p2 を持つアンプの伝達特性は,
Ao(s) = 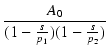
|
(312) |
のように表せます.
ここで,2つの極の周波数比を表す 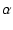 (極の分離係数)を導入します.
これは,いわゆるスタガ比のことです.
これを用いると,ゲインの式は次のように表せます.
(極の分離係数)を導入します.
これは,いわゆるスタガ比のことです.
これを用いると,ゲインの式は次のように表せます.
Ao(s) = 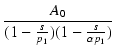
|
(314) |
帰還率  の負帰還をかけた後のゲイン Af(s) は,
の負帰還をかけた後のゲイン Af(s) は,
低域の帰還量を
F0 = 1 + A0 とおくと,
とおくと,
Af(s) = 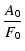 . . 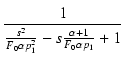
|
(315) |
この式の第2項と式(290)の係数を比較することにより,
の関係が成り立ち,これらの式より,
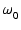 |
= |
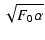 | p1| | p1| |
(318) |
| Q |
= |
- 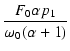 |
|
| |
= |
- 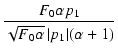 |
|
| |
= |
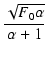 |
(319) |
となります.
したがって,2つのポールを持つアンプに負帰還をかけると,
その伝達関数はやはり2次になります.
負帰還をかけた後のゲインのピークを目標値にコントロールするには,
式(294)より目標とする Q を求め,
式(319)を満たす 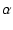 を求め,
極の比が
を求め,
極の比が 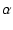 になるように位相補償を施せばよいことになります.
になるように位相補償を施せばよいことになります.
式(319)より,
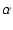 + 1 + 1 |
= |
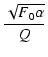 |
|
(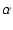 +1)2 +1)2 |
= |
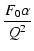 |
|
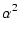 +2(1 - +2(1 - 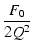 ) )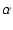 + 1 + 1 |
= |
0 |
(320) |
となり,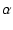 > 1 となる解は,
ですが,
F0/2Q2
> 1 となる解は,
ですが,
F0/2Q2 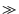 1 の場合,
と近似できます.
T0 は,低域のループゲイン A0
1 の場合,
と近似できます.
T0 は,低域のループゲイン A0 です.
です.
負帰還をかける前の位相余裕を知るために,
ループゲインが1になる周波数 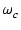 を求めます.
ループゲイン T(s) は,
を求めます.
ループゲイン T(s) は,
| T(s) |
= |
A(s)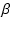 |
|
| |
= |
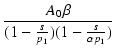 |
|
| |
= |
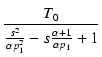 |
(323) |
T(j ) ) |
= |
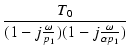 |
(324) |
| |
= |
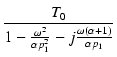 |
(325) |
ですから,ループゲインの絶対値は,
| T(j )| = )| = ![$\displaystyle {\frac{{T_0}}{{\sqrt{\bigl(1-\frac{\omega^2}{\alpha p_1^2}\bigr)^2 + \bigl[\frac{\omega(\alpha+1)}{\alpha p_1}\bigr]^2}}}}$](img710.png)
|
(326) |
ループゲインが1となる周波数 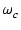 は,
は,
 1 - 1 - 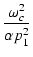 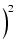 + + 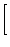 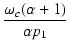 ![$\displaystyle \Bigr]^{2}_{}$](img714.png) - T02 - T02 |
= |
0 |
|
1 - 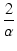  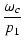 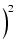 + + 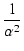  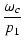 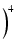 + +  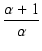 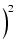  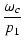 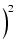 - T02 - T02 |
= |
0 |
|
 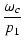 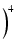 + ( + (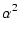 +1) +1) 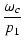 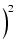 + (1 - T02) + (1 - T02)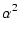 |
= |
0 |
|
式(322)を代入して,
T02 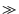 1,
T0/Q2
1,
T0/Q2 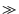 1 ならば,近似的に,
これより,
1 ならば,近似的に,
これより,
ループゲインの位相は,式(324)より,
arg T(j ) = tan-1 ) = tan-1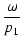 + tan-1 + tan-1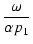
|
(328) |
したがって,ゲイン交点周波数 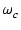 における位相余裕
における位相余裕 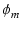 は,
は,
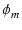 |
= |
180o + arg T(j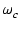 ) ) |
|
| |
= |
180o + tan-1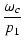 + tan-1 + tan-1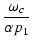 |
|
式(327)より,
T0/Q2 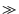 1 ならば
1 ならば
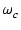 /p1
/p1 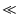 - 1 なので,
- 1 なので,
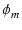 |
= |
180o -90o + tan-1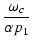 |
|
| |
= |
90o + tan-1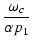 |
(329) |
となります.
次に,負帰還をかけた後の -3 dB 周波数 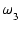 を求めます.
式(315)より,
を求めます.
式(315)より,
| Af(s) |
= |
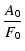 . . 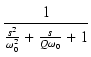 |
|
Af(j ) ) |
= |
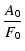 . . 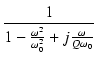 |
|
| Af(j )| )| |
= |
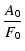 . . 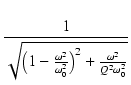 |
(330) |
-3 dB 点では,根号の中が 2 となるので,
が成り立ちます.
したがって,
 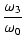 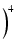 -2 -2 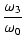 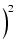 +1 + +1 + 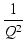  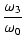 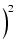 - 2 - 2 |
= |
0 |
|
 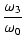 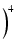 +2 +2 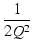 -1 -1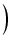  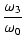 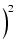 - 1 - 1 |
= |
0 |
|
これを解くと,
式(316)に,
式(322)を代入して,
これを式(332)に代入して整理すると,
利得交点周波数 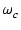 に対する -3 dB 点の周波数の比は,
式(334)と式(327)より,
に対する -3 dB 点の周波数の比は,
式(334)と式(327)より,
この結果をいくつかの Q について求めると,次の表のようになります.
|
(1) Q |
(2)
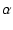 = p2/p1 = p2/p1 |
(3)
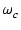 /p1 /p1 |
(4)
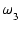 / /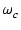 |
(5)
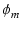 = 90o + tan-1 = 90o + tan-1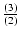 |
Ap (dB) |
(%) |
|
1.0 |
T0 |
-0.79T0 |
1.62 |
51.8o |
1.25 |
16.3 |
|
0.9 |
1.23T0 |
-0.83T0 |
1.61 |
56.1o |
0.69 |
12.3 |
|
0.8 |
1.56T0 |
-0.87T0 |
1.59 |
60.8o |
0.21 |
8.1 |
|
0.707 |
2T0 |
-0.91T0 |
1.55 |
65.5o |
0 |
4.3 |
|
0.6 |
2.78T0 |
-0.95T0 |
1.46 |
71.2o |
0 |
0.9 |
|
0.5 |
4T0 |
-0.97T0 |
1.32 |
76.3o |
0 |
0 |
たとえば,最初のポールが 10kHz にあるアンプに 20dB の負帰還(F0 = 10)をかけて,ピークが生じないようにするには,Q = 0.7 にする必要があります.
T0 = 9 より,必要なスタガ比は 18 で,第2のポールは 180kHz でなければなりません.
このとき,ゲイン交点周波数は 82kHz であり,
帰還後のカットオフ周波数は,
82 x 1.55 = 127 kHz になります.
なお,この解析ではいたるところで近似を行っていますので,
誤差は10%程度はあるでしょう.
より正確な情報が必要な場合は,SPICEでシミュレーションを行います.


Next: 10 位相補償
Up: オーディオのための交流理論入門
Previous: 8 能動素子の等価回路とポール
Ayumi Nakabayashi
平成19年12月8日
![]() 倍(通常は
倍(通常は
![]()
![]() 1)し,
それを入力から差し引くものです.
1)し,
それを入力から差し引くものです.
![]() 回路ともいう)は受動素子,
特に抵抗を使って構成する場合が多く,
回路ともいう)は受動素子,
特に抵抗を使って構成する場合が多く,
![]() に周波数特性がない場合が多いのですが,
ここでは
に周波数特性がない場合が多いのですが,
ここでは ![]() (s) として,周波数特性がある場合も考えます.
(s) として,周波数特性がある場合も考えます.
![]() 回路は左側から右側に信号を伝えないことが仮定されていますが,
そのような仮定が成り立たない場合には,
漸近利得という概念を使って解析します.
オーディオにおいては,通常は上述の仮定が成り立っていますので,
漸近利得による解析は,ここでは扱いません.
興味のある方は,[2], [1]などを参照してください.
回路は左側から右側に信号を伝えないことが仮定されていますが,
そのような仮定が成り立たない場合には,
漸近利得という概念を使って解析します.
オーディオにおいては,通常は上述の仮定が成り立っていますので,
漸近利得による解析は,ここでは扱いません.
興味のある方は,[2], [1]などを参照してください.
![]() が十分大きければ,
が十分大きければ,
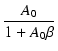 =
= 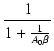
![]() 回路の入力の間で切断するのがよいでしょう.
DCアンプなど,負帰還がないと動作点が定まらないような場合は,
インダクタなどを入れて,直流には負帰還がかかり,
交流信号には負帰還がかからないような措置を施す必要があります.
切断する適切な箇所がアンプ内にある場合もあります.
回路の入力の間で切断するのがよいでしょう.
DCアンプなど,負帰還がないと動作点が定まらないような場合は,
インダクタなどを入れて,直流には負帰還がかかり,
交流信号には負帰還がかからないような措置を施す必要があります.
切断する適切な箇所がアンプ内にある場合もあります.
![]() 180o 以下であれば,安定です.
また別の言い方をすれば,位相が
180o 以下であれば,安定です.
また別の言い方をすれば,位相が
![]() 180o に達するまでに,
ループゲインが 0dB 以下になっていれば,安定です.
ただし,安定といっても発振しないというだけで,
周波数特性にピークができることはあります.
180o に達するまでに,
ループゲインが 0dB 以下になっていれば,安定です.
ただし,安定といっても発振しないというだけで,
周波数特性にピークができることはあります.
![]() 180o との差です.
ゲイン余裕は,ループゲインの位相が
180o との差です.
ゲイン余裕は,ループゲインの位相が
![]() 180o になったときの,
ループゲインと 0dB との差です.
180o になったときの,
ループゲインと 0dB との差です.
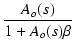
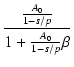
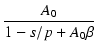
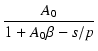
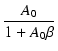 .
. 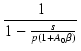
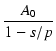 =
= 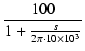
![]() vo =
vo = ![]() Ao になります.
ゲイン交点周波数では,ループゲインの絶対値が1になりますが,
これは
Ao になります.
ゲイン交点周波数では,ループゲインの絶対値が1になりますが,
これは ![]() Ao の絶対値が1になることを意味しています.
また
Ao の絶対値が1になることを意味しています.
また ![]() Ao とx軸の負方向とでなす角が位相余裕
Ao とx軸の負方向とでなす角が位相余裕 ![]() になります.
位相余裕が 60o のときのベクトル図を図102に示します.
になります.
位相余裕が 60o のときのベクトル図を図102に示します.
![]() でゲインの絶対値が1で,
周波数が低くなるにつれて
+6 dB/oct でゲインが上昇し続ける積分回路と,
通常のRCによるローパス特性を組み合わせて,
でゲインの絶対値が1で,
周波数が低くなるにつれて
+6 dB/oct でゲインが上昇し続ける積分回路と,
通常のRCによるローパス特性を組み合わせて,
![]() においてオープンループゲインの絶対値が1となり,
その時の位相余裕が希望の値になるような回路を考えます.
この回路に
においてオープンループゲインの絶対値が1となり,
その時の位相余裕が希望の値になるような回路を考えます.
この回路に ![]() = 1 の全帰還をかけた場合のゲインを求めます.
全帰還をかけた場合の低域のゲインは1です.
= 1 の全帰還をかけた場合のゲインを求めます.
全帰還をかけた場合の低域のゲインは1です.
![]() の場合,
第2のポールによる位相の遅れ
の場合,
第2のポールによる位相の遅れ ![]() は,
は,
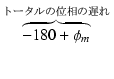 =
=  +
+ 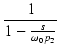
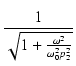
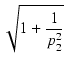

![]() のとき,ゲインの特性にピークは見られません.
Q = 1/
のとき,ゲインの特性にピークは見られません.
Q = 1/![]() のとき,最大平坦振幅特性が得られ,
これは2次のバタワース特性と呼ばれます.
Q > 1/
のとき,最大平坦振幅特性が得られ,
これは2次のバタワース特性と呼ばれます.
Q > 1/![]() のとき,周波数特性にピークが生じますが,
このピークの周波数
のとき,周波数特性にピークが生じますが,
このピークの周波数 ![]() を求めてみます.
式(291)をさらに変形すると,
を求めてみます.
式(291)をさらに変形すると,
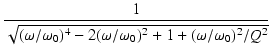
![$\displaystyle {\frac{{1}}{{\sqrt{[(\omega/\omega_0)^2-(1-1/2Q^2)]^2+1-(1-1/2Q^2)^2}}}}$](img652.png)
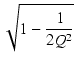
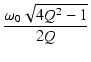
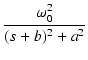
![$\displaystyle {\frac{{\omega_0^2}}{{s[(s+b)^2+a^2]}}}$](img661.png)
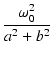 [1 - e-bt(cos at +
[1 - e-bt(cos at + ![]() t について微分すると,
t について微分すると,
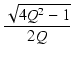
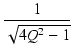 sin
sin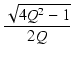
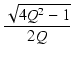 sin
sin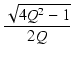
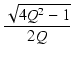
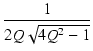 +
+ 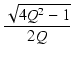
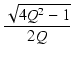
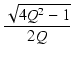
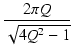
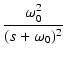
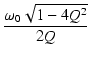
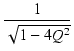 sinh
sinh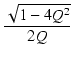
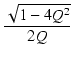
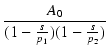
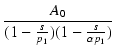
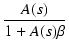
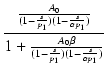
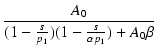
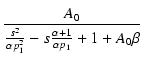
![]() を求め,
極の比が
を求め,
極の比が ![]() になるように位相補償を施せばよいことになります.
になるように位相補償を施せばよいことになります.
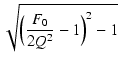
![]() を求めます.
ループゲイン T(s) は,
を求めます.
ループゲイン T(s) は,
![$\displaystyle {\frac{{T_0}}{{\sqrt{\bigl(1-\frac{\omega^2}{\alpha p_1^2}\bigr)^2 + \bigl[\frac{\omega(\alpha+1)}{\alpha p_1}\bigr]^2}}}}$](img710.png)
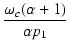
![]() を求めます.
式(315)より,
を求めます.
式(315)より,
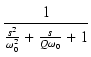
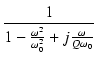
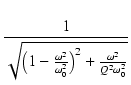
![$\displaystyle {\frac{{2Q^2 \bigl[ 1-\frac{1}{2Q^2} + \sqrt{\bigl(1-\frac{1}{2Q^2}\bigr)^2+1} \bigr]}}{{-1+\sqrt{1 + 4Q^4}}}}$](img737.png)