next up previous
Next: 9 負帰還 Up: オーディオのための交流理論入門 Previous: 7 伝達関数 2次の場合

8 能動素子の等価回路とポール

8.1 真空管の等価回路

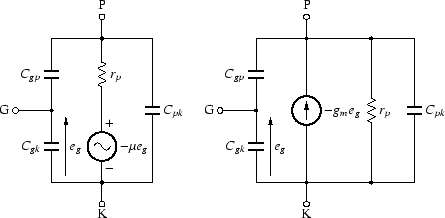
電極間容量を含めた真空管の等価回路は， 図62のようになります． 左側は電圧源による等価回路で，主に三極管に使い， 右側は電流源による等価回路で，主に五極管に使いますが， 両者ともまったく等価なので，どちらを使ってもかまいません．

図 62: 真空管の等価回路
\begin{figure}\input{figs/tube_eqv} \end{figure}

8.2 能動素子一般の等価回路

真空管，バイポーラトランジスタ(BJT)，電界効果トランジスタ(FET)の等価回路は， すべて図63で表されます．

図 63: 能動素子の等価回路
\begin{figure}\input{figs/active_eqv} \end{figure}

それぞれの素子の値は，以下のようになります．

汎用モデル 真空管 BJT FET
rx 0 rb 0
r$\scriptstyle \it in$ $ \infty$ r$\scriptstyle \pi$ $ \infty$
C$\scriptstyle \it in$ Cgk C$\scriptstyle \pi$ Cgs
Cf Cgp C$\scriptstyle \mu$ Cgd
Co Cpk Co Cds
ro rp ro ro

8.3 増幅回路の等価回路

実際の回路から等価回路に変換するには，次の手順で行います．

  1. 能動素子の代わりに，図63をあてはめる．
  2. 電源(電圧源)は短絡し，電流源は開放する． 電源のインピーダンスの影響を調べる場合は，この限りではない．
  3. コンデンサ，コイルに関しては， 分析の目的，周波数帯域に応じて適宜短絡したり，開放したりする．
  4. テブナンの定理，ノートンの定理などを使って，素子の数を減らす．

図64のような，2段のカソード接地電圧増幅回路を例にします． 入力のボリューム Rg1 は，後述のミラー効果によりもっとも高域特性が悪くなる 半分の位置に設定します．

図 64: 2段カソード接地電圧増幅回路
\begin{figure}\input{figs/volamp_sch} \end{figure}

この回路に能動素子の等価回路をあてはめると， 図65のようになります．

図 65: 能動素子を等価回路で置き換える
\begin{figure}\input{figs/volamp_eqv1} \end{figure}

今回は，電源のインピーダンスを0とするので，電源を短絡します．

図 66: 電源を短絡
\begin{figure}\input{figs/volamp_eqv2} \end{figure}

8.4 中域の等価回路

中域では，カップリングコンデンサ Cc1, Cc2 およびカソードバイパスコンデンサ Ck1, Ck2 は短絡と見なせます． また，電極間容量は開放とみなせます． 入力からV2のグリッドまでの等価回路は， 図67のようになります．
図 67: 中域の等価回路
\begin{figure}\input{figs/eqv_mid} \end{figure}

V1のグリッド，すなわち Rg1a と Rg1b の接続点から左側のインピーダンス Rs を調べると，

Rs = Rg1a//Rg1b = $\displaystyle {\frac{{R_{g1}}}{{4}}}$ (211)
であり， この点に負荷をつながない，開放時の電圧 v0 は，

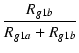v0 = $\displaystyle {\frac{{R_{g1b}}}{{R_{g1a}+R_{g1b}}}}$vi = $\displaystyle {\frac{{v_i}}{{2}}}$ (212)
となりますから，テブナンの定理により， 図68(a)のように簡略化されます．
図 68: 中域の等価回路(2)
\begin{figure}\input{figs/eqv_mid2} \end{figure}
出力側の3個の抵抗は並列接続ですので，その合成値を R2 = ro1//Rp1//Rg2 とおけば， 等価回路は図68(b)のように簡略化されます．

これより，

v1 = $\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$v0 (213)
v2 = - gmv1R2  
  = - v0$\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$gmR2 (214)

となり，v0 から v2 への中域のゲイン AM は，

AM = $\displaystyle {\frac{{v_2}}{{v_0}}}$ = - $\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$gmR2 (215)
となります． 今回は，能動素子が真空管なので， r$\scriptstyle \it in$ = $ \infty$ ですから，

AM = - gmR2 (216)
となります．

8.5 低域の等価回路

低域では，カップリングコンデンサ Cc1, Cc2 のインピーダンスが無視できなくなってきます． ここでは，カソードバイパスコンデンサ Ck1, Ck2 は十分に大きく，インピーダンスを無視できるとします． 等価回路は，図69のようになります． ここで， R2' = ro//Rp1 です．
図 69: 低域の等価回路
\begin{figure}\input{figs/eqv_lo} \end{figure}

これより，

v2 = - gmv1{R2'//(1/sCc1 + Rg2)}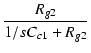$\displaystyle {\frac{{R_{g2}}}{{1/s C_{c1}+R_{g2}}}}$  
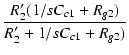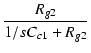  = - gmv1$\displaystyle {\frac{{R_2'(1/s C_{c1}+R_{g2})}}{{R_2'+ 1/s C_{c1} + R_{g2})}}}$ . $\displaystyle {\frac{{R_{g2}}}{{1/s C_{c1}+R_{g2}}}}$  
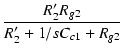  = - gmv1$\displaystyle {\frac{{R_2' R_{g2}}}{{R_2'+ 1/s C_{c1} + R_{g2}}}}$  
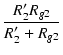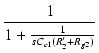  = - gmv1$\displaystyle {\frac{{R_2' R_{g2}}}{{R_2'+R_{g2}}}}$ . $\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(R_2' + R_{g2})}}}}$  
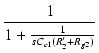  = - gmR2v1$\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(R_2' + R_{g2})}}}}$  
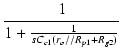TL(s) = AM$\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(r_o//R_{p1} + R_{g2})}}}}$ (217)

となって，時定数が Cc1(ro//Rp1 + Rg2) の1次のハイパス特性であることがわかります．

真空管の場合，より直感的に求めるには，電圧源による等価回路を使います．

図 70: 低域の等価回路(2)
\begin{figure}\input{figs/eqv_lo2} \end{figure}
図70(a)のA点より左側のインピーダンスと開放時の電圧から， テブナンの定理を使って(b)のように変形し， 抵抗とコンデンサを入れ替えると(c)になります． この回路の v3 は v1 に対してローパス特性であり， 時定数は Cc1(ro//Rp1 + Rg2) であることは明らかです． v1 と v2 の関係は，
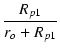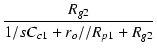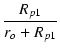v2 = - $\displaystyle {\frac{{R_{p1}}}{{r_o+R_{p1}}}}$$\displaystyle \mu$v1 . $\displaystyle {\frac{{R_{g2}}}{{1/sC_{c1}+r_o//R_{p1}+R_{g2}}}}$  
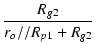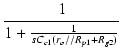  = - $\displaystyle \mu$v1$\displaystyle {\frac{{R_{p1}}}{{r_o+R_{p1}}}}$ . $\displaystyle {\frac{{R_{g2}}}{{r_o//R_{p1}+R_{g2}}}}$ . $\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(r_o//R_{p1} + R_{g2})}}}}$  
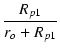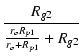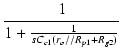  = - v1gmro$\displaystyle {\frac{{R_{p1}}}{{r_o+R_{p1}}}}$ . $\displaystyle {\frac{{R_{g2}}}{{\frac{r_o R_{p1}}{r_o + R_{p1}}+R_{g2}}}}$ . $\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(r_o//R_{p1} + R_{g2})}}}}$  
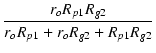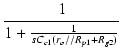  = - v1gm$\displaystyle {\frac{{r_oR_{p1}R_{g2}}}{{r_o R_{p1} + r_o R_{g2} + R_{p1} R_{g2}}}}$ . $\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(r_o//R_{p1} + R_{g2})}}}}$  
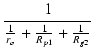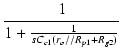  = - v1gm$\displaystyle {\frac{{1}}{{\frac{1}{r_o} + \frac{1}{R_{p1}} + \frac{1}{R_{g2}}}}}$ . $\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(r_o//R_{p1} + R_{g2})}}}}$  
  = - v1gm(ro//Rp1//Rg2) . 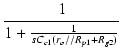$\displaystyle {\frac{{1}}{{1 + \frac{1}{s C_{c1}(r_o//R_{p1} + R_{g2})}}}}$ (218)

となり，先程の結果と一致します．

8.5.1 数値例

V1として12AX7を使い， Vbb = 200 V, Rp1 = 220 kΩ, Rk1 = 3.3 kΩ, Rg2 = 470 kΩ, Ck1 = 47 μF, Cc1 = 0.1 μF とします． このとき，V1の動作点は， Ep = 115.9 V, Eg = - 1.24 V, Ip = 0.38 mA であり， 三定数は， $ \mu$ = 95.6, rp = 89.4 kΩ, gm = 1.07 mS です．

これより，

R2' = rp//Rp1 = 89.4 x 103//220 x 103 = 63.6 x 103 [Ω]  
R2 = rp//Rp1//Rg2 = 89.4 x 103//220 x 103//470 x 103 = 56 x 103 [Ω]  
AM = - gmR2' = 1.07 x 10-3 . 56 x 103 = - 60  
p = - 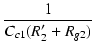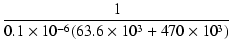$\displaystyle {\frac{{1}}{{C_{c1}(R_2' + R_{g2})}}}$ = - $\displaystyle {\frac{{1}}{{0.1\times10^{-6}(63.6\times10^3 + 470\times10^3)}}}$ = - 18.7 [rad /s] = - 3 [Hz]  

となります． 周波数特性は，図71のようになります．
図 71: カップリングコンデンサによる低域特性
\includegraphics{figs/cc_freq.ps}
SPICEによるシミュレーションは，図72のようになります．

scr_AC81.png

図 72: カップリングコンデンサによる低域特性のシミュレーション
\begin{figure}. % \end{figure}

8.6 カソードバイパスコンデンサの影響

ここでは，カップリングコンデンサ Cc1 が十分大きな場合を考えます． カソードからグラウンドの間のインピーダンスを Zk とすると， 等価回路は，図73のようになります．

図 73: カソードにインピーダンスを入れた等価回路
\begin{figure}\input{figs/eqv_zk1} \end{figure}

電流源から電圧源に変更し，負荷をまとめて R2 = Rp1//Rg2 とすると， 等価回路は，図74のようになります．

図 74: カソードにインピーダンスを入れた等価回路(2)
\begin{figure}\input{figs/eqv_zk2} \end{figure}

この等価回路から，

v0 = v1 + v2 (219)
i = $\displaystyle {\frac{{\mu v_1}}{{Z_k + r_{o1} + R_2}}}$ (220)
v2 = iZk (221)
vo = - iR2 (222)

が成り立ちます． 式(219)より，

v1 = v0 - v2

これを式(220)に代入して，

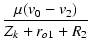
i = $\displaystyle {\frac{{\mu (v_0 - v_2)}}{{Z_k + r_{o1} + R_2}}}$

これを式(221)に代入すると，
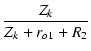v2 = $\displaystyle \mu$(v0 - v2)$\displaystyle {\frac{{Z_k}}{{Z_k + r_{o1} + R_2}}}$  
v2{(1 + $\displaystyle \mu$)Zk + ro1 + R2} = $\displaystyle \mu$v0Zk  
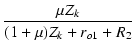v2 = $\displaystyle {\frac{{\mu Z_k}}{{(1 + \mu)Z_k + r_{o1} + R_2}}}$v0 (223)

これらを使うと，出力電圧は，
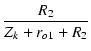vo = - $\displaystyle \mu$(v0 - v2)$\displaystyle {\frac{{R_2}}{{Z_k + r_{o1} + R_2}}}$  
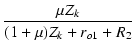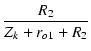  = - $\displaystyle \mu$v0$\displaystyle \Bigl[$1 - $\displaystyle {\frac{{\mu Z_k}}{{(1 + \mu)Z_k + r_{o1} + R_2}}}$$\displaystyle \Bigr]$$\displaystyle {\frac{{R_2}}{{Z_k + r_{o1} + R_2}}}$  
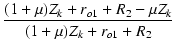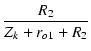  = - $\displaystyle \mu$v0$\displaystyle {\frac{{(1 + \mu)Z_k + r_{o1} + R_2 - \mu Z_k}}{{(1 + \mu)Z_k + r_{o1} + R_2}}}$ . $\displaystyle {\frac{{R_2}}{{Z_k + r_{o1} + R_2}}}$  
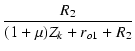  = - $\displaystyle \mu$v0$\displaystyle {\frac{{R_2}}{{(1 + \mu)Z_k + r_{o1} + R_2}}}$ (224)

となります． これを等価回路で表すと，図75のようになります． すなわち，カソード側に入っているインピーダンスは，(1 + $ \mu$) 倍して，プレート側にあるとして分析できます．
図 75: カソードにインピーダンスを入れた等価回路(3)
\begin{figure}\input{figs/eqv_zk3} \end{figure}

つまり，抵抗値は (1 + $ \mu$) 倍に，コンデンサの容量は 1/(1 + $ \mu$) 倍にしてプレート側に移します． このようにして得られた等価回路は，図76のようになります．

図 76: カソードにインピーダンスを入れた等価回路(4)
\begin{figure}\input{figs/eqv_zk4} \end{figure}

したがって，Ck1 と Rk1 の並列部分のインピーダンスを Z とおけば，

Z = 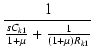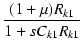$\displaystyle {\frac{{1}}{{\frac{s C_{k1}}{1+\mu} + \frac{1}{(1+\mu)R_{k1}}}}}$ = $\displaystyle {\frac{{(1+\mu)R_{k1}}}{{1+sC_{k1}R_{k1}}}}$ (225)
v0 から vo への伝達関数は，
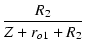T(s) = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{Z + r_{o1} + R_2}}}$  
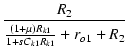  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{\frac{(1+\mu)R_{k1}}{1+sC_{k1}R_{k1}} + r_{o1} + R_2}}}$  
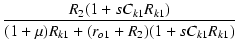  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2(1+sC_{k1}R_{k1})}}{{(1+\mu)R_{k1} + (r_{o1} + R_2)(1+sC_{k1}R_{k1})}}}$  
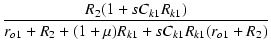  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2(1+sC_{k1}R_{k1})}}{{r_{o1} + R_2 + (1+\mu)R_{k1} + sC_{k1}R_{k1}(r_{o1} + R_2)}}}$  
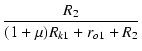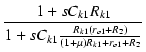  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{(1+\mu)R_{k1}+r_{o1}+R_2}}}$ . $\displaystyle {\frac{{1+sC_{k1}R_{k1}}}{{1 + sC_{k1}\frac{R_{k1}(r_{o1} + R_2)}{(1+\mu)R_{k1}+r_{o1}+R_2}}}}$  
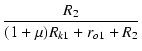  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{(1+\mu)R_{k1}+r_{o1}+R_2}}}$ . $\displaystyle {\frac{{1+sC_{k1}R_{k1}}}{{1 + sC_{k1}\frac{R_{k1}(r_{o1} + R_2)/(1+\mu)}{[(1+\mu)R_{k1}+r_{o1}+R_2]/(1+\mu)}}}}$  
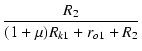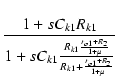  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{(1+\mu)R_{k1}+r_{o1}+R_2}}}$ . $\displaystyle {\frac{{1+sC_{k1}R_{k1}}}{{1 + sC_{k1}\frac{R_{k1}\frac{r_{o1} + R_2}{1+\mu}}{R_{k1}+\frac{r_{o1}+R_2}{1+\mu}}}}}$  
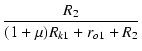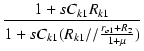  = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{(1+\mu)R_{k1}+r_{o1}+R_2}}}$ . $\displaystyle {\frac{{1+sC_{k1}R_{k1}}}{{1 + sC_{k1}(R_{k1}//\frac{r_{o1} + R_2}{1+\mu})}}}$ (226)

したがって，この回路の低域のゲインは A0 = - $ \mu$R2/[(1 + $ \mu$)Rk1 + ro1 + R2] で， ゼロとポールは，
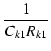z = - $\displaystyle {\frac{{1}}{{C_{k1}R_{k1}}}}$ (227)
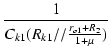p = - $\displaystyle {\frac{{1}}{{C_{k1}(R_{k1}//\frac{r_{o1} + R_2}{1+\mu})}}}$ (228)

で，| z| < | p| ですから，周波数特性は，図77のようになります．
図 77: カソードバイパスコンデンサの影響
\begin{figure}\input{figs/zk_freq} \end{figure}

8.6.1 数値例

V1として12AX7を使い， Vbb = 200 V, Rp1 = 220 kΩ, Rk1 = 3.3 kΩ, Rg2 = 470 kΩ, Ck1 = 47 μF, Cc1 = 0.1 μF とします． このとき，V1の動作点は， Ep = 115.9 V, Eg = - 1.24 V, Ip = 0.38 mA であり， 三定数は， $ \mu$ = 95.6, rp = 89.4 kΩ, gm = 1.07 mS です．

これより，

R2 = Rp1//Rg2 = 220 x 103 . 470 x 103 = 150 x 103 [Ω]  
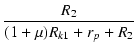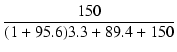A0 = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{(1+\mu)R_{k1}+r_p+R_2}}}$ = - 95.6$\displaystyle {\frac{{150}}{{(1+95.6)3.3+89.4+150}}}$ = - 25.7  
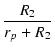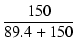AM = - $\displaystyle \mu$$\displaystyle {\frac{{R_2}}{{r_p+R_2}}}$ = - 95.6$\displaystyle {\frac{{150}}{{89.4+150}}}$ = - 60  
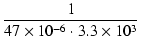z = - $\displaystyle {\frac{{1}}{{47\times10^{-6} \cdot 3.3\times10^3}}}$ = - 6.4 [rad /s] = - 1.03 [Hz]  
p = - 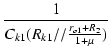$\displaystyle {\frac{{1}}{{C_{k1}(R_{k1}//\frac{r_{o1} + R_2}{1+\mu})}}}$ = - 15 [rad /s] = 2.4 [Hz]  

となります． 周波数特性は，図78のようになります．
図 78: カソードバイパスコンデンサによる低域特性
\includegraphics{figs/ck_freq.ps}
SPICEによるシミュレーションは，図79のようになります．

scr_AC82.png

図 79: カソードバイパスコンデンサによる低域特性のシミュレーション
\begin{figure}. % \end{figure}

8.7 高域の等価回路--ミラー効果

高域の等価回路は，V2の入力容量を無視すれば，図80(a)のようになります． 入力信号の部分にテブナンの定理を使い，負荷の抵抗をまとめると，(b)のようになります．

図 80: 高域の等価回路
\begin{figure}\input{figs/eqv_mil1} \end{figure}

このとき，点Aから Cf に流れる電流 i1 は，

i1 = $\displaystyle {\frac{{v_1 - v_2}}{{X_{C_f}}}}$ = (v1 - v2)sCf (229)
となります． v1 から v2 への伝達関数には s が含まれるのですが， これを中域のゲイン AM で一定と仮定すれば，

v2 = AMv1 = - gmR2v1 (230)
これを，式(229)に代入すると，

i1 = (1 + gmR2)v1sCf = v1s(1 + gmR2)Cf = v1s(1 + | AM|)Cf (231)
となり， CM = (1 + | AM|)Cf とおけば， この容量のコンデンサがA点からグラウンドにつながれたように見えます(図81)． このように，Cf が増幅器のゲイン倍されて入力容量に付加されることを， 発見者の名前をとってミラー効果(Miller effect)といいます． この等価回路は，入力側の周波数特性を近似したものであり， Cf を通して入力から出力へ，あるいは出力から入力へ信号が伝達されることを無視しています5．
図 81: ミラー効果
\begin{figure}\input{figs/eqv_mil2} \end{figure}

この等価回路より， Ct = C$\scriptstyle \it in$ + CM とおけば，

v1 = 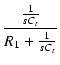$\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ . $\displaystyle {\frac{{\frac{1}{sC_t}}}{{R_1+\frac{1}{sC_t}}}}$v0  
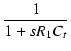  = $\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ . $\displaystyle {\frac{{1}}{{1+sR_1C_t}}}$v0  
v2 = - gmv1(R2//$\displaystyle {\frac{{1}}{{s C_o}}}$)  
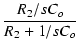  = - gmv1$\displaystyle {\frac{{R_2/sC_o}}{{R_2+1/sC_o}}}$  
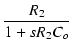  = - gmv1$\displaystyle {\frac{{R_2}}{{1+sR_2C_o}}}$  
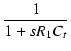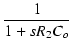  = - v0$\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ . gmR2 . $\displaystyle {\frac{{1}}{{1+sR_1C_t}}}$ . $\displaystyle {\frac{{1}}{{1+sR_2C_o}}}$  
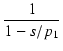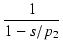  = - v0$\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ . gmR2 . $\displaystyle {\frac{{1}}{{1-s/p_1}}}$ . $\displaystyle {\frac{{1}}{{1-s/p_2}}}$ (233)

となります． ここで，
p1 = - $\displaystyle {\frac{{1}}{{R_1C_t}}}$ = - $\displaystyle {\frac{{1}}{{[(R_s+r_x)//r_{\it in}] \cdot [C_{\it in}+(1+g_m R_2)C_f]}}}$ (234)
p2 = - $\displaystyle {\frac{{1}}{{R_2C_o}}}$ = - $\displaystyle {\frac{{1}}{{(r_{o1}//R_{p1}//R_{g2}) C_o}}}$ (235)

です．

8.7.1 数値例

V1として12AX7を使い， Vbb = 200 V, Rp1 = 220 kΩ, Rk1 = 3.3 kΩ, Rg2 = 470 kΩ, Ck1 = 47 μF, Cc1 = 0.1 μF とします． このとき，V1の動作点は， Ep = 115.9 V, Eg = - 1.24 V, Ip = 0.38 mA であり， 三定数は， $ \mu$ = 95.6, rp = 89.4 kΩ, gm = 1.07 mS です． 12AX7の電極間容量は， Cgk = 1.6 pF, Cgp = 1.6 pF, Cpk = 0.33 pF です．

したがって，

R2 = rp//Rp1//Rg2 = (89.4//220//470) x 103 = 56 x 103 [Ω]  
| AM| = gmR2 = 1.07 x 10-3 . 56 x 103 = 60  
Ct = C$\scriptstyle \it gk$ + (1 + | AM|)Cgp = [1.6 + (1 + 60)1.6] x 10-12 = 99.2 [pF]  
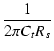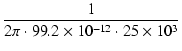fc = $\displaystyle {\frac{{1}}{{2\pi C_t R_s}}}$ = $\displaystyle {\frac{{1}}{{2\pi \cdot 99.2\times10^{-12} \cdot 25\times10^3}}}$ = 64.3 x 103 [Hz]  

となります．

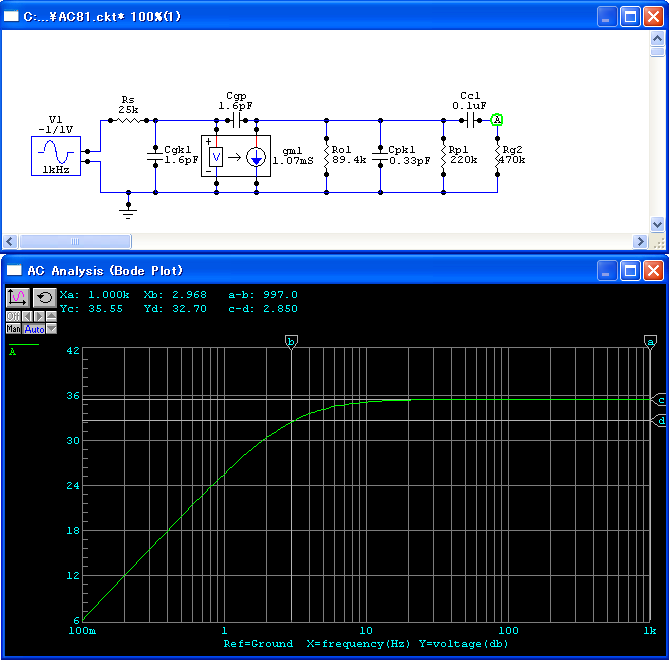
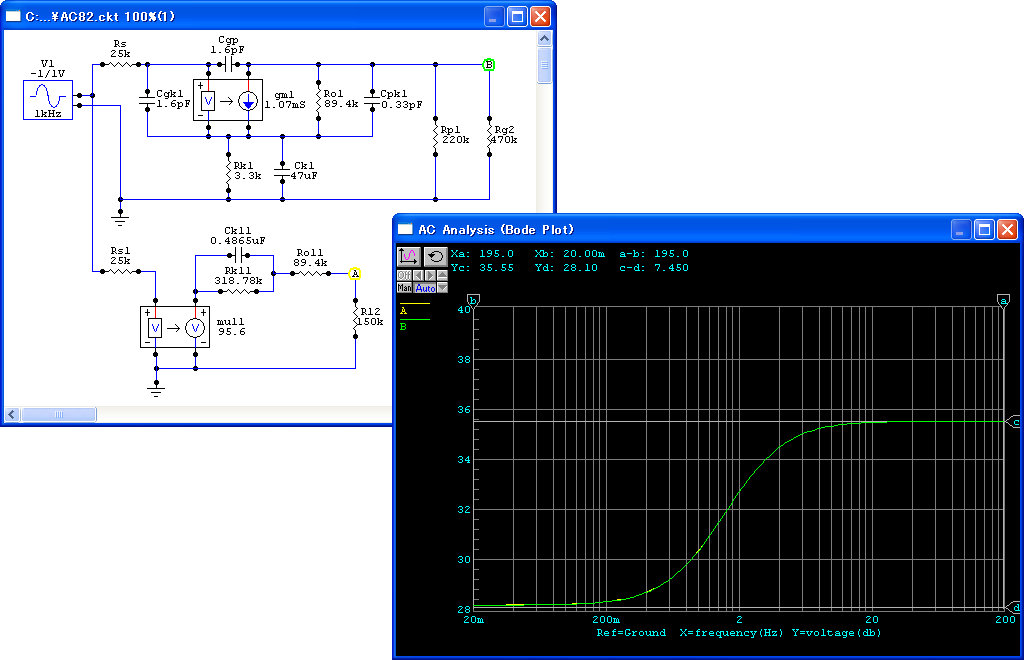
SPICEによるシミュレーションは，図82のようになります．

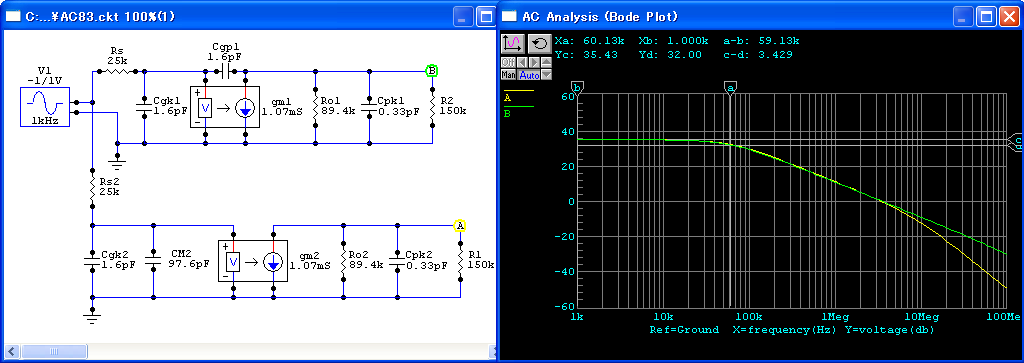
scr_AC83.png

図 82: 高域特性のシミュレーション
\begin{figure}. % \end{figure}
上側の等価回路(グラフは緑)は正確なもので， 下側の等価回路(グラフは黄)はミラー効果による近似です． 黄色の線は2回折れ曲がり，ポールが2つあることを示しています． 緑色の線は1回しか折れ曲がっていないように見えますが， 実はたいへんなことが起きています． それは，次の正確な解析でわかります．


8.8 正確な高域の解析

高域の等価回路(図80(a))において， A点より左側を見たインピーダンスは，

R1 = (Rs + rx)//r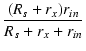$\scriptstyle \it in$ = $\displaystyle {\frac{{(R_s+r_x)r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ (236)
で，短絡した電流は，

ii = $\displaystyle {\frac{{v_0}}{{R_s+r_x}}}$ (237)
ですから，定電流源を使って(b)のように書き換えられます．
図 83: 高域の等価回路
\begin{figure}\input{figs/eqv_hi1} \end{figure}
ここで，
C1 = C$\scriptstyle \it in$  
C2 = Co  
R2 = ro//Rp1//Rg2  

です．

ここで，点Xについて，キルヒホッフの電流則を適用すると，

ii = $\displaystyle {\frac{{v_1}}{{R_1}}}$ + v1sC1 + (v1 - v2)sCf (238)
  = v1$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{R_1}}}$ + sC1 + sCf$\displaystyle \Bigr)$ - v2sCf (239)

また，点Yについて，キルヒホッフの電流則を適用すると，
(v1 - v2)sCf = gmv1 + $\displaystyle {\frac{{v_2}}{{R_2}}}$ + v2sC2 (240)
v1(sCf - gm) = v2$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{R_2}}}$ + sC2 + sCf$\displaystyle \Bigr)$  
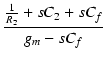v1 = - $\displaystyle {\frac{{\frac{1}{R_2} + s C_2 + s C_f}}{{g_m - s C_f}}}$v2 (241)

これを，式(239)に代入して，
ii = - v2$\displaystyle {\frac{{\frac{1}{R_2} + s C_2 + s C_f}}{{g_m - s C_f}}}$$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{R_1}}}$ + sC1 + sCf$\displaystyle \Bigr)$ - v2sCf  
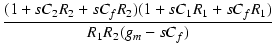  = - v2$\displaystyle \left[\vphantom{ \frac{(1 + sC_2R_2 + sC_fR_2)(1 + sC_1R_1 + sC_fR_1)}{R_1R_2(g_m-sC_f)} + s C_f }\right.$$\displaystyle {\frac{{(1 + sC_2R_2 + sC_fR_2)(1 + sC_1R_1 + sC_fR_1)}}{{R_1R_2(g_m-sC_f)}}}$ + sCf$\displaystyle \left.\vphantom{ \frac{(1 + sC_2R_2 + sC_fR_2)(1 + sC_1R_1 + sC_fR_1)}{R_1R_2(g_m-sC_f)} + s C_f }\right]$  
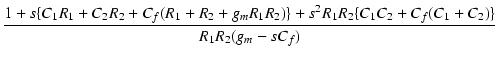  = - v2$\displaystyle {\frac{{1 + s\{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)\} + s^2R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}{{R_1R_2(g_m-sC_f)}}}$ (242)


T(s) = $\displaystyle {\frac{{v_2}}{{v_0}}}$ = $\displaystyle {\frac{{v_2}}{{i_i(R_s+r_x)}}}$  
  = - $\displaystyle {\frac{{1}}{{R_s+r_x}}}$  
      x $\displaystyle {\frac{{R_1R_2(g_m-sC_f)}}{{1 + s\{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)\} + s^2R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}}$  
  = - $\displaystyle {\frac{{1}}{{R_s+r_x}}}$ . $\displaystyle {\frac{{(R_s+r_x)r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$gmR2  
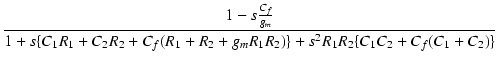      x $\displaystyle {\frac{{1-s\frac{C_f}{g_m}}}{{1 + s\{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)\} + s^2R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}}$  
  = - gmR2$\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$  
      x $\displaystyle {\frac{{1-s\frac{C_f}{g_m}}}{{1 + s\{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)\} + s^2R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}}$ (243)

中域のゲインを AM とおけば，

AM = - gmR2$\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ (244)
で，
T(s) = AM$\displaystyle {\frac{{1-s\frac{C_f}{g_m}}}{{1 + s\{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)\} + s^2R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}}$  
  = AMT'(s) (245)

と書けます． T'(s) の分母 D'(s) は，D'(s) = 0 の解を p1, p2 とすれば， 次のように表せます．
D'(s) = $\displaystyle \Bigl($1 - $\displaystyle {\frac{{s}}{{p_1}}}$$\displaystyle \Bigr)$$\displaystyle \Bigl($1 - $\displaystyle {\frac{{s}}{{p_2}}}$$\displaystyle \Bigr)$  
  = 1 - s$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{p_1}}}$ + $\displaystyle {\frac{{1}}{{p_2}}}$$\displaystyle \Bigr)$ + $\displaystyle {\frac{{s^2}}{{p_1p_2}}}$  

p1 と p2 が大きく離れている( | p1| $ \ll$ | p2|)ときは，次のように近似できます．

D'(s) $\displaystyle \approx$ 1 - $\displaystyle {\frac{{s}}{{p_1}}}$ + $\displaystyle {\frac{{s^2}}{{p_1p_2}}}$ (246)
これより，主要極(dominant pole) p1 は，

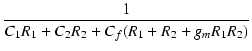
p1 $\displaystyle \approx$ - $\displaystyle {\frac{{1}}{{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)}}}$ (247)
と近似できます． この式と，ミラー効果による式(234)を比較すると， C2R2 および CfR2 だけ異なっていることがわかります． さらに， gmR2 $ \gg$ 1 なので，

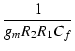
p1 $\displaystyle \approx$ - $\displaystyle {\frac{{1}}{{g_mR_2R_1C_f}}}$ (248)
と近似できます． また，第2のポール p2 は，
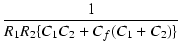p1p2 = $\displaystyle {\frac{{1}}{{R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}}$  
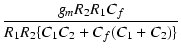p2 $\displaystyle \approx$ - $\displaystyle {\frac{{g_mR_2R_1C_f}}{{R_1R_2\{C_1C_2+C_f(C_1+C_2)\}}}}$  
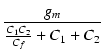  $\displaystyle \approx$ - $\displaystyle {\frac{{g_m}}{{\frac{C_1C_2}{C_f}+C_1+C_2}}}$ (249)

となります．

ここで，Cf を大きくしていくと， 第1のポールは，低い方に移動し， 第2のポールは，高い方に移動し， Cf$ \to$$ \infty$ のとき， C2$ \to$ - gm/(C1 + C2) となります． このように，Cf によって，2つの極が離れる現象を極分離(pole split)といい，負帰還の位相補償に大いに役立ちます． また，Cf$ \to$ 0 のとき，

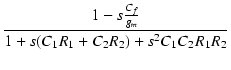T'(s) = $\displaystyle {\frac{{1-s\frac{C_f}{g_m}}}{{1+s(C_1R_1+C_2R_2)+s^2C_1C_2R_1R_2}}}$  
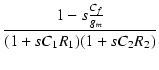  = $\displaystyle {\frac{{1-s\frac{C_f}{g_m}}}{{(1+sC_1R_1)(1+sC_2R_2)}}}$ (250)

となるので， p1$ \to$ -1/C1R1, p2$ \to$ -1/C2R2 となります．

一方，伝達関数の分子にはゼロがありますが，その値は，

z = $\displaystyle {\frac{{g_m}}{{C_f}}}$ (251)
で，符号は正です． この周波数より上ではゲインが 6 dB/oct で上昇し， 位相は通常のゼロとは逆に，遅れます． 通常のゼロは負帰還を安定な方向に変化させますが， このゼロにより負帰還は不安定になります． このような実部が正のゼロを右半平面のゼロといいますが， これは，ゼロやポールを複素平面上にプロットしたときに， 原点より右側にくるからです．

8.8.1 数値例

V1として12AX7を使い， Vbb = 200 V, Rp1 = 220 kΩ, Rk1 = 3.3 kΩ, Rg2 = 470 kΩ, Ck1 = 47 μF, Cc1 = 0.1 μF とします． このとき，V1の動作点は， Ep = 115.9 V, Eg = - 1.24 V, Ip = 0.38 mA であり， 三定数は， $ \mu$ = 95.6, rp = 89.4 kΩ, gm = 1.07 mS です． 12AX7の電極間容量は， Cgk = 1.6 pF, Cgp = 1.6 pF, Cpk = 0.33 pF です．

したがって，

R1 = (Rs + rx)//r$\scriptstyle \it in$ = 25 x 103 [Ω]  
R2 = rp//Rp1//Rg2 = (89.4//220//470) x 103 = 56 x 103 [Ω]  
p1 = - 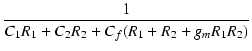$\displaystyle {\frac{{1}}{{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)}}}$  
  = - $\displaystyle {\frac{{1}}{{[1.6\cdot 25 + 0.33\cdot 56 + 1.6(25 + 56 + 1.07 \cdot 25 \cdot 56)] \times 10^{-9}}}}$  
  = -387000 [rad /s] = - 61.6 x 103 [Hz]  
p2 = - 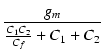$\displaystyle {\frac{{g_m}}{{\frac{C_1C_2}{C_f}+C_1+C_2}}}$ = - $\displaystyle {\frac{{1.07\times10^{-3}}}{{[\frac{1.6\cdot 0.33}{1.6}+1.6+0.33]\times10^{-12}}}}$  
  = -473 x 106 [rad /s] = - 75 x 106 [Hz]  
z = 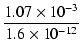$\displaystyle {\frac{{g_m}}{{C_f}}}$ = $\displaystyle {\frac{{1.07\times10^{-3}}}{{1.6\times10^{-12}}}}$ = 669 x 106 [rad /s] = 106 x 106 [Hz]  

となります．

Cf を変化させたときのポールとゼロの変化を， 図84に示します． ポールは赤で，ゼロは青で示しています． Cf が電極間容量のみの場合の周波数特性を， 図85に示します． ポールとゼロの位置に縦線を引いてあります． 位相は最大 270o 遅れます．

図: Cfを変化させたときのポールとゼロの変化(12AX7)
\includegraphics{figs/ax7_hi1.ps}
図: 周波数特性(12AX7)
\includegraphics{figs/ax7_hi1_freq.ps}
真空管では gm が低いので， Cf を増やすと p2 よりも z の影響が先に現われるようになります．

Co に次段の入力容量を含め 30pF としたときのポールとゼロの変化を， 図86に示します．

図: Cfを変化させたときのポールとゼロの変化(12AX7, Co=30pF)
\includegraphics{figs/ax7_hi2.ps}
図: 周波数特性(12AX7)
\includegraphics{figs/ax7_hi2_freq.ps}
出力容量(次段の入力容量)が増えた場合，p2 が下がりますが， p1 や z にはそれほど大きな変化がありません． 多少は極分離の恩恵を受けることができます．

トランジスタの典型的な値では， 例えば， Rs = 100 kΩ, rx = 50 Ω, r$\scriptstyle \it in$ = 4.6 kΩ, gm = 38.5 mS, ro = 100 kΩ, C$\scriptstyle \it in$ = 47 pF, Cf = 2.6 pF, Co = 0.8 pF, Rc1 = 100 kΩ とすれば，

R1 = (Rs + rx)//r$\scriptstyle \it in$ = (100 x 103 +50)//4.6 x 103 = 4.4 x 103 [Ω]  
R2 = ro//Rc1 = 100 x 103//100 x 103 = 50 x 103 [Ω]  
p1 = - 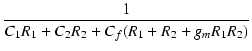$\displaystyle {\frac{{1}}{{C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)}}}$  
  = - $\displaystyle {\frac{{1}}{{[47\cdot 4.4 + 0.8\cdot 50 + 2.6(4.4 + 50 + 38.5 \cdot 4.4 \cdot 50)] \times 10^{-9}}}}$  
  = -44600 [rad /s] = - 7.1 [kHz]  
p2 = - 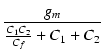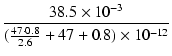$\displaystyle {\frac{{g_m}}{{\frac{C_1C_2}{C_f}+C_1+C_2}}}$ = - $\displaystyle {\frac{{38.5\times10^{-3}}}{{(\frac{47\cdot 0.8}{2.6}+47+0.8)\times10^{-12}}}}$  
  = -618 x 106 [rad /s] = - 98 x 106 [Hz]  
z = 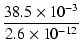$\displaystyle {\frac{{g_m}}{{C_f}}}$ = $\displaystyle {\frac{{38.5\times10^{-3}}}{{2.6\times10^{-12}}}}$ = 14.8 x 109 [rad /s] = 2.4 x 109 [Hz]  

となります． トランジスタの場合，gm が非常に大きいので， ゼロは問題にならないほど大きくなります．

Cf を変化させたときのポールとゼロの変化を， 図88に示します．

図 88: Cfを変化させたときのポールとゼロの変化(BJT)
\includegraphics{figs/tr_hi1.ps}
図 89: 周波数特性(BJT)
\includegraphics{figs/tr_hi1_freq.ps}
トランジスタの場合，gm が大きいので，ゼロの存在はほとんど無視できます．

8.8.2 何が起こっているのか?

グリッドの電圧 v1 を見ることにより，なにが起こっているのか調べてみましょう． 式(241)より，

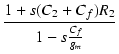v1 = - $\displaystyle {\frac{{1}}{{g_m R_2}}}$ . $\displaystyle {\frac{{1 + s(C_2+C_f)R_2}}{{1 - s\frac{C_f}{g_m}}}}$v2

これに式(243)を代入して，

v1 = $\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ . $\displaystyle {\frac{{1 + s(C_2+C_f)R_2}}{{1+s[C_1R_1+C_2R_2+C_f(R_1+R_2+g_mR_1R_2)] +s^2R_1R_2[C_1C_2+C_f(C_1+C_2)]}}}$v0

この式の第2項の分母の解を p1, p2 とおき，
z = $\displaystyle {\frac{{g_m}}{{C_f}}}$  
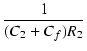p3 = - $\displaystyle {\frac{{1}}{{(C_2+C_f)R_2}}}$  

とおけば，
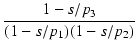v1 = $\displaystyle {\frac{{r_{\it in}}}{{R_s+r_x+r_{\it in}}}}$ . $\displaystyle {\frac{{1 - s/p_3}}{{(1 - s/p_1)(1 - s/p_2)}}}$v0 (252)
v2 = - gmR2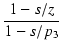$\displaystyle {\frac{{1 - s/z}}{{1 - s/p_3}}}$v1 (253)

となります． これより，各段のゲインは図90のようになります．
図 90: 高域の周波数特性
\begin{figure}\input{figs/eqv_hi_gain} \end{figure}
低域から | p1| までのゲインは平坦で， そこからミラー効果により高域が落ち始めます． それは，グリッドに並列にミラー容量が付加されるためです． さらに周波数が上がると，出力側の容量 C2 + Cf のインピーダンスが下がり， 出力が減ってきます． この角周波数が | p3| です． こうなると，能動素子のゲインが減ってくるので， ミラー効果も減ってきて，グリッドにおける減衰が一定になります． これらの働きが合成されて， -6 dB/oct でゲインが下がり続けます．

角周波数 z では，能動素子による増幅 gm と，Cf を左から右へと通り抜ける電流が同じになります． これ以上の周波数では，能動素子の働きは失われています．

8.9 2段アンプの特性

図91の定数の，2段のアンプの周波数特性を検討しましょう．

図 91: 2段カソード接地電圧増幅回路
\begin{figure}\input{figs/volamp_sch2} \end{figure}

V1の三定数は $ \mu$ = 95.6, rp = 89.4 kΩ, gm = 1.07 mS で， V2の三定数は $ \mu$ = 96.8, rp = 73.2 kΩ, gm = 1.32 mS です．

等価回路は，図92のようになります．

図 92: 2段カソード接地電圧増幅回路の等価回路
\begin{figure}\input{figs/volamp2_eqv} \end{figure}
ここで，
v0 = $\displaystyle {\frac{{v_i}}{{2}}}$  
R1 = $\displaystyle {\frac{{R_{g1}}}{{4}}}$  
R2 = rp1//Rp1//Rg2  
R3 = rp2//Rp2//Rg3  
C1 = Cgk1  
Cf1 = Cgp1  
C2 = Cpk1 + Cgk2  
Cf2 = Cgp2  
C3 = Cpk2  

です． 点A, B, Cについて，キルヒホッフの電流則を適用すると，
ii = $\displaystyle {\frac{{v_1}}{{R_1}}}$ + v1sC1 + (v1 - v2)sCf1 (254)
(v1 - v2)sCf1 = gm1v1 + $\displaystyle {\frac{{v_2}}{{R_2}}}$ + v2sC2 + (v2 - v3)sCf2 (255)
(v2 - v3)sCf2 = gm2v2 + $\displaystyle {\frac{{v_3}}{{R_3}}}$ + v3sC3 (256)

が得られ，v0 から v3 への伝達関数 T(s) を求めると，

T(s) = gm1R2gm2R3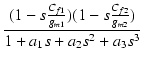$\displaystyle {\frac{{(1-s\frac{C_{f1}}{g_{m1}})(1-s\frac{C_{f2}}{g_{m2}})}}{{1 + a_1s + a_2s^2 + a_3s^3}}}$ (257)
となります． ここで，
a1 = C1R1 + C2R2 + C3R3 + Cf1[R2 + R1(1 + gm1R2)] + Cf2[R3 + R2(1 + gm2R3)] (258)
a2 = C1C2R1R2 + C1C3R1R3 + C2C3R2R3 + Cf1(C1 + C2)R1R2 + Cf2(C2 + C3)R2R3  
      + C1Cf2R1[R3 + R2(1 + gm2R3)] + C3Cf1R3[R2 + R1(1 + gm1R2)]  
      + Cf1Cf2[R1R2(1 + gm2R3) + R1R3(1 + gm1R2)] (259)
a3 = R1R2R3[C1C2(C3 + Cf2) + C1C3(Cf1 + Cf2)  
      + C1Cf1Cf2 + C2C3Cf1 + Cf1Cf2(C2 + C3)] (260)

です． 分母多項式 D(s) は，その根 p1, p2, p3 により因数分解できて，
D(s) = (1 - s/p1)(1 - s/p2)(1 - s/p3)  
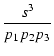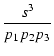
  = 1 - s$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{p_1}}}$ + $\displaystyle {\frac{{1}}{{p_2}}}$ + $\displaystyle {\frac{{1}}{{p_2}}}$$\displaystyle \Bigr)$ + s2$\displaystyle \Bigl($$\displaystyle {\frac{{1}}{{p_1p_2}}}$ + $\displaystyle {\frac{{1}}{{p_2p_3}}}$ + $\displaystyle {\frac{{1}}{{p_1p_3}}}$$\displaystyle \Bigr)$ - $\displaystyle {\frac{{s^3}}{{p_1p_2p_3}}}$  

であり， | p1| $ \ll$ | p2| $ \ll$ | p3| なら，

D(s) $\displaystyle \approx$ 1 - $\displaystyle {\frac{{s}}{{p_1}}}$ + $\displaystyle {\frac{{s^2}}{{p_1p_2}}}$ - $\displaystyle {\frac{{s^3}}{{p_1p_2p_3}}}$

と近似できます． これより，
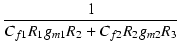p1 $\displaystyle \approx$ - $\displaystyle {\frac{{1}}{{a_1}}}$ = - $\displaystyle {\frac{{1}}{{C_{f1}R_1g_{m1}R_2+C_{f2}R_2g_{m2}R_3}}}$ (261)
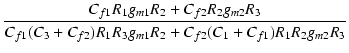p2 $\displaystyle \approx$ - $\displaystyle {\frac{{a_1}}{{a_2}}}$ = - $\displaystyle {\frac{{C_{f1}R_1g_{m1}R_2+C_{f2}R_2g_{m2}R_3}}{{C_{f1}(C_3+C_{f2})R_1R_3g_{m1}R_2+C_{f2}(C_1+C_{f1})R_1R_2g_{m2}R_3}}}$ (262)
p3 $\displaystyle \approx$ - $\displaystyle {\frac{{a_2}}{{a_3}}}$ (263)

となり，最初の2つのポールの見当をつけることができます．

各段の伝達特性を求めると，

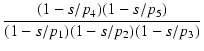$\displaystyle {\frac{{v_1}}{{v_0}}}$ = $\displaystyle {\frac{{(1-s/p_4)(1-s/p_5)}}{{(1-s/p_1)(1-s/p_2)(1-s/p_3)}}}$ (264)
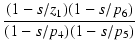$\displaystyle {\frac{{v_2}}{{v_1}}}$ = - gm1R2$\displaystyle {\frac{{(1-s/z_1)(1-s/p_6)}}{{(1-s/p_4)(1-s/p_5)}}}$ (265)
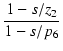$\displaystyle {\frac{{v_3}}{{v_2}}}$ = - gm2R3$\displaystyle {\frac{{1-s/z_2}}{{1-s/p_6}}}$ (266)

で，p1, p2, p3 は，D(s) の根，
z1 = $\displaystyle {\frac{{g_{m1}}}{{C_{f1}}}}$ (267)
z2 = $\displaystyle {\frac{{g_{m2}}}{{C_{f2}}}}$ (268)
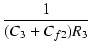p6 = - $\displaystyle {\frac{{1}}{{(C_3+C_{f2})R_3}}}$ (269)

で，p4, p5 は，

1 + s{C2R2 + C3R3 + Cf1R2 + Cf2[R3 + R2(1 + gm2R3)]} + s2R2R3[C2(C3 + Cf2) + C3(Cf1 + Cf2) + Cf1Cf2] = 0

の解で，近似値を求めれば，
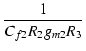p4 $\displaystyle \approx$ - $\displaystyle {\frac{{1}}{{C_{f2}R_2g_{m2}R_3}}}$ (270)
p5 $\displaystyle \approx$ - $\displaystyle {\frac{{g_{m2}R_3}}{{R_3[(C_{f1}+C_2)(1+\frac{C_3}{C_{f2}})+C_3]}}}$ (271)

となります．

周波数特性は，図93のようになります．

図 93: 2段アンプの周波数特性
\includegraphics{figs/volamp2_freq.ps}
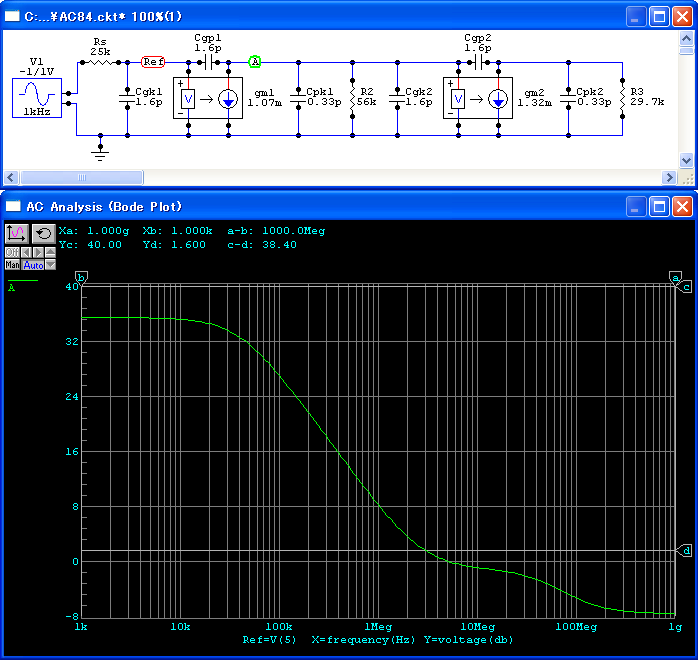
V2のゲイン(A23)が下がってくると，V2のミラー効果が減ってきて， 前段のゲイン(A12)にゼロが生じ，ゲインが一定となります． 同様に，V1のゲイン(A12)が下がってくると，V1のミラー効果が減ってきて， V1のグリッドまでのゲイン(A1)にゼロが生じます． 入力からV1の出力までの特性はA2で， 第1のポールからゲインが直線的に下がっています． これにV2のゲイン(A23)が加わるので， 全体のゲイン(A3)には2箇所の折れ曲がり(| p1|, | p2|)が生じます．

この程度の規模になると，計算で特性を求めるよりシミュレーションを使ったほうが手軽でしょう． 回路と結果は，図94のようになります．

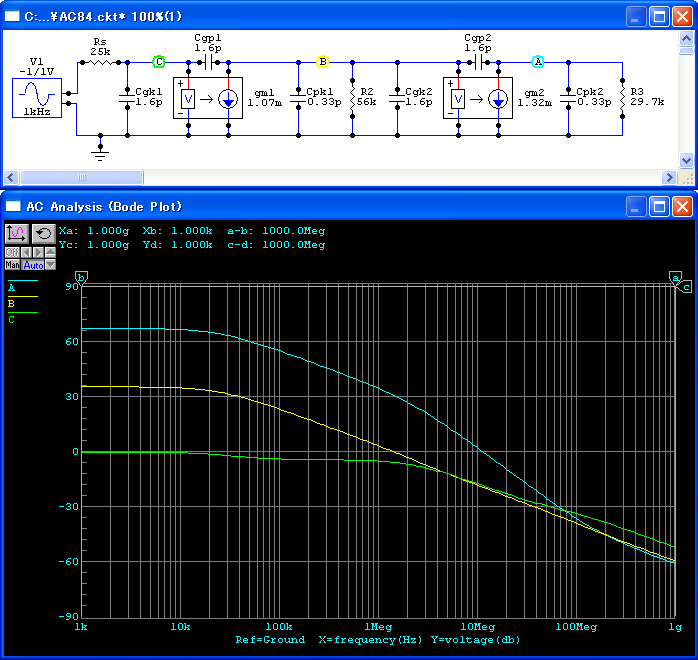
scr_AC84_1.png

図 94: 2段アンプのシミュレーション
\begin{figure}. % \end{figure}

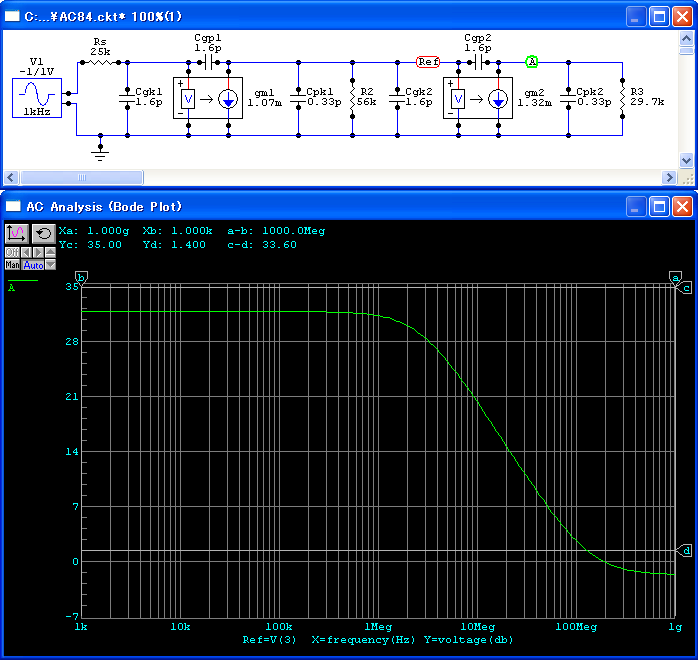
V1, V2の単体の周波数特性を表示するには， Ctrlを押しながら，マウスでクリックすることにより基準点(Refと表示されている)を設定できます． 残念ながら基準点は1箇所しか設定できませんので， V1とV2それぞれで表示させなくてはなりません． V1の周波数特性を図95に， V2の周波数特性を図96に示します．

scr_AC84_2.png

図 95: V1の周波数特性
\begin{figure}. % \end{figure}

scr_AC84_3.png

図 96: V2の周波数特性
\begin{figure}. % \end{figure}
next up previous
Next: 9 負帰還 Up: オーディオのための交流理論入門 Previous: 7 伝達関数 2次の場合
Ayumi Nakabayashi
平成19年12月8日