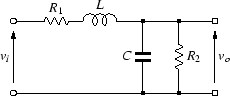 |
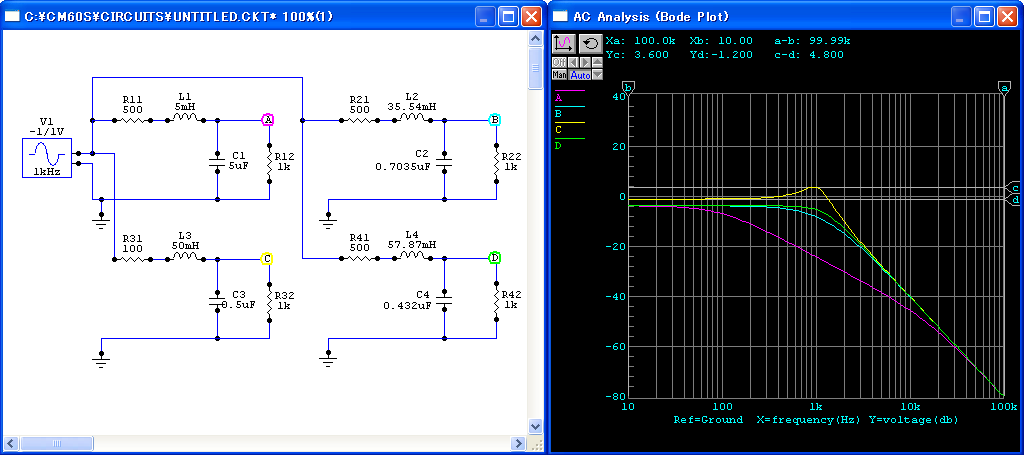
図48のような,抵抗とコイルとコンデンサを組み合わせた回路を考えます.
この回路の伝達関数を求めます.
C と R2 の並列の部分のインピーダンスを Z とすると,
| Z | = | 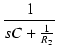 |
|
| = | 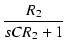 |
(184) |
| T(s) | = | 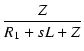 |
|
| = | 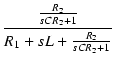 |
||
| = | 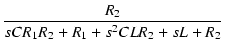 |
||
| = |  |
||
| = |  . . 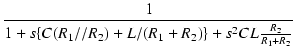 |
(185) |
この伝達関数の振る舞いを知るため, 次の形の伝達関数を調べます.
T(s) = 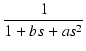
|
(186) |
| D = b2 - 4a | (187) |
T(s) = 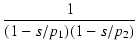
|
(188) |
| a | = | CL = 5 x 10-6 . 5 x 10-3 = 5 x 10-6 . 5 x 10-3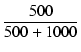 = 1.67 x 10-8 = 1.67 x 10-8 |
|
| b | = | C(R1//R2) + 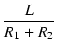 = 5 x 10-6(500//1000) + = 5 x 10-6(500//1000) + 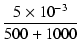 = 1.67 x 10-3 = 1.67 x 10-3 |
| p1 = - 602.4, p2 = - 99600 | (189) |
|
f1 = |
(190) |
ゲインの周波数特性を求めるRの関数は,次のようになります.
function (R1=500, L=5e-3, C=5e-6, R2=1e3)
{
f <- dec(10, 100e3, 30)
s <- 2 * pi * f * (0+1i)
XL <- s * L
XC <- 1/(s * C)
Z <- XC %p% R2
T <- Z / (R1 + XL + Z)
semilogplot(f, dB(T), type="l", col="red",
ylim=c(-70, 10), yaxs="i",
xlab="Frequency (Hz)", ylab="Gain (dB)")
}
T(s) = 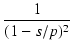
|
(191) |
| a | = | CL = 0.7035 x 10-6 . 35.54 x 10-3 = 0.7035 x 10-6 . 35.54 x 10-3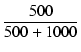 = 1.67 x 10-8 = 1.67 x 10-8 |
|
| b | = | C(R1//R2) + 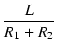 = 0.7035 x 10-6(500//1000) + = 0.7035 x 10-6(500//1000) + 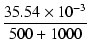 = 2.58 x 10-4 = 2.58 x 10-4 |
| p = - 7740 | (192) |
|
f = |
(193) |
| = | (194) | ||
| Q | = | (195) |
T(s) = 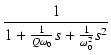
|
(196) |
|
D = b2 -4a = |
(197) |
| D' = |
< | 0 | |
| < | 4 | ||
| Q2 | > | ||
| Q | > | (198) |
ゲインを求めると,
| = | 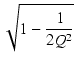 |
(201) | |
| Apeak | = | 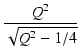 |
(202) |
| 1 - |
> | 0 | |
| < | 1 | ||
| 2Q2 | > | 1 | |
| Q2 | > | ||
| Q | > | (203) |
また,
![]() =
= ![]() のとき,
式(199)より,
のとき,
式(199)より,
| T(j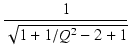 = Q = Q
|
(204) |
| a | = | CL = 0.5 x 10-6 . 50 x 10-3 = 0.5 x 10-6 . 50 x 10-3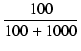 = 2.27 x 10-8 = 2.27 x 10-8 |
|
| b | = | C(R1//R2) + 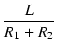 = 0.5 x 10-6(100//1000) + = 0.5 x 10-6(100//1000) + 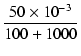 = 9.09 x 10-5 = 9.09 x 10-5 |
|
| = | |||
| Q | = |
| = | 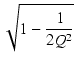 |
||
| Apeak | = | 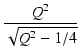 = 1.74 = 1.74 |
バタワース特性となるのは, たとえば, R1 = 500 Ω, L = 57.87 mH, C = 0.432 μF, R2 = 1 kΩ のときで,特性は,図54のようになります. このとき,カットオフ周波数におけるゲインは -3 dB となります.
2次の伝達関数は,次のように表すこともあります.
T(s) = 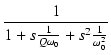 = = 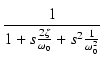 = = 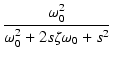
|
(205) |
|
|
(206) |
Q, ![]() と特性の関係を,以下に示します.
と特性の関係を,以下に示します.
| Q |
< |
|
... |
|
> |
| > 1 | 1 | ... |
|
< |
|
| 解 | 実2 | 実1 | 複素数 | ||
| ピーク | なし | あり | |||
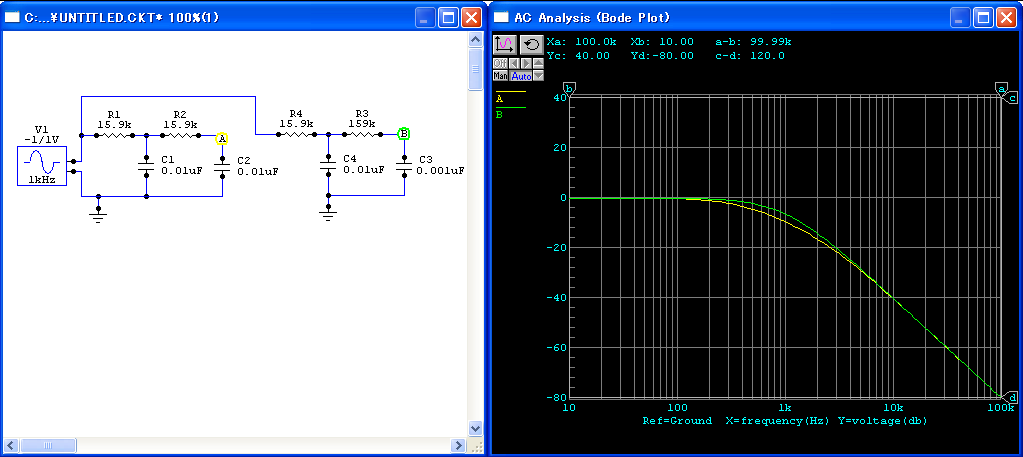
伝達関数は,次のようになります.
T(s) = 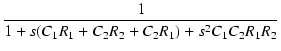
|
(207) |
| = | 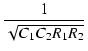 |
(208) | |
| Q | = | 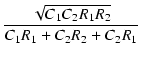 |
(209) |
R1 = R2, C1 = C2 とすると,Q = 1/3 となります. 図56の赤い線が,この場合です.
R2 = 10R1, C2 = C1/10 とすると,
Q = 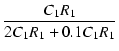 = = |
(210) |
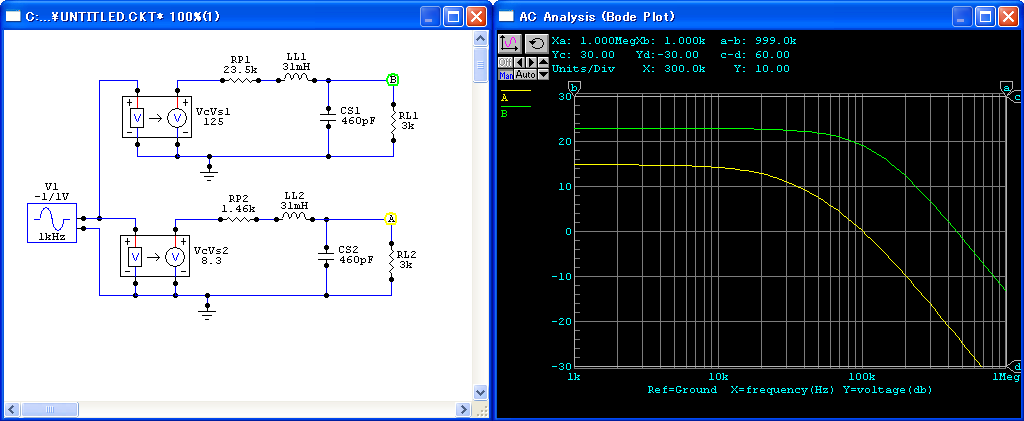
東栄変成器のシングル用出力トランスT-850 7kの
3 kΩ タップの
漏れインダクタンス Ll,浮遊容量 Cs は,実測値で,
| RL | = | 3 kΩ | |
| Ll | = | 31 mH | |
| Cs | = | 460 pF |
まず五極管接続ですが,
動作点を
Ep = 200 V,
Eg2 = 200 V,
Eg = - 15.3 V,
Ip = 35 mA とすれば,三定数は
![]() = 125,
gm = 5.3 mS,
rp = 23.5 kΩ となります.
したがって,
= 125,
gm = 5.3 mS,
rp = 23.5 kΩ となります.
したがって,
| = | 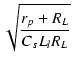 = 125 [kHz] = 125 [kHz] |
||
| Q | = | 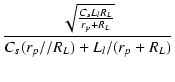 = 0.53 = 0.53 |
三極管接続の場合,
動作点を
Ep = 200 V,
Eg = - 16.5 V,
Ip = 35 mA とすれば,三定数は
![]() = 8.3,
gm = 5.7 mS,
rp = 1.46 kΩ となります.
したがって,
= 8.3,
gm = 5.7 mS,
rp = 1.46 kΩ となります.
したがって,
| = | 51 [kHz] | ||
| Q | = | 0.42 |
今回の例ではピークが生じませんでしたが, 五極管接続では場合によってはピークが生じることもあるでしょう.
2次の負荷を開放にすると,特に三極管接続の場合にピークが生じやすくなります.