

Next: 7 伝達関数 2次の場合
Up: オーディオのための交流理論入門
Previous: 5 複素数
これまで,伝達関数には,変数として j を使ってきましたが,
これからは,これを s で表します.
今回は扱いませんが,この s はラプラス変数で,
ラプラス変換を使えば過渡応答を求めることもできます.
正弦波に対する定常的な応答を求めるには,s に j
を使ってきましたが,
これからは,これを s で表します.
今回は扱いませんが,この s はラプラス変数で,
ラプラス変換を使えば過渡応答を求めることもできます.
正弦波に対する定常的な応答を求めるには,s に j を代入してやります.
を代入してやります.
この記号を使うと,コンデンサのインピーダンス ZC は,
ZC = 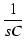
|
(131) |
と表せ,コイルのインピーダンス ZL は,
と表せます.
これから基本となる4つの1次の伝達関数を見ていきます.
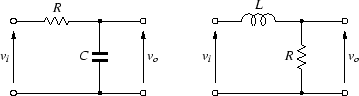
次の2つの回路は,1次のローパス特性になります.
図 35:
ローパス特性の回路
 |
左側のCRによるローパスフィルタの伝達関数は,
CR = TC とおくと,
T(s) = 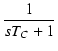
|
(134) |
となります.この TC は時定数(time constant)と呼ばれます.
右側のLRによるローパスフィルタの伝達関数は,
L/R = TL とおくと,
T(s) = 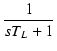
|
(136) |
となり,CRの場合と同じ形になりました.
一般に,1次のローパス特性の伝達関数は,
T(s) = 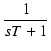
|
(137) |
となり,p = - 1/T とおけば,
T(s) = 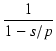
|
(138) |
となります.
この p は伝達関数の極(ポール) (pole)といいます.
s = p のとき,T が無限大になるからです.
現実には,p は複素数ではありませんので,
この伝達関数 T が無限大になることはありません.
一般に,伝達関数の分母 D(s) が0となる解をポールといいいます.
伝達関数の分母の多項式は,ポール
p1, p2,... によって,次のように変形できます.
| D(s) |
= |
1 + a1s + a2s2 + a3s3 + ... |
(139) |
| |
= |
(1 - s/p1)(1 - s/p2)(1 - s/p3) ... |
(140) |
この伝達関数の,ゲインと位相の周波数特性を調べてみましょう.
そのために,
 = - p とおき,s = j
= - p とおき,s = j を代入し,有理化します.
を代入し,有理化します.
ゲインは,
となります.

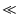
 のとき,
のとき,
 /
/
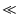 1 となり,分母はほぼ 1 ですので,
| T|
1 となり,分母はほぼ 1 ですので,
| T| 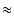 1 となります.
1 となります.
 =
=  のとき,分母は
のとき,分母は 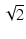 となるので,
| T| = 1/
となるので,
| T| = 1/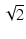 となります.
これをデシベルで表すと約 -3 dB で,
fc =
となります.
これをデシベルで表すと約 -3 dB で,
fc =  /2
/2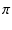 はカットオフ周波数と呼ばれます.
はカットオフ周波数と呼ばれます.

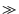
 のとき,
のとき,
 /
/
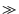 1 となり,分母の根号の中の 1 を無視することができるので,
| T|
1 となり,分母の根号の中の 1 を無視することができるので,
| T| 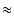 1/(
1/( /
/ ) =
) =  /
/ となります.
したがって,周波数が10倍となるごとにゲインは1/10になり,
-20 dB/dec または
-6 dB/oct でゲインが直線的に下がります.
となります.
したがって,周波数が10倍となるごとにゲインは1/10になり,
-20 dB/dec または
-6 dB/oct でゲインが直線的に下がります.
位相は,
arg T(j ) = tan-1 ) = tan-1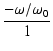 = tan-1 = tan-1 - - 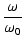 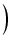
|
(143) |
となり,

 0 で 0o,
0 で 0o,
 =
=  で -45o,
で -45o,

 で -90o となります.
で -90o となります.
グラフで表すと,図36のようになります.
次の2つの回路は,1次のハイパス特性になります.
図 37:
ハイパス特性の回路
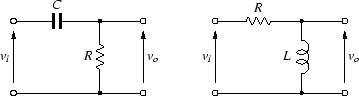 |
左側のCRによるハイパスフィルタの伝達関数は,
CR = TC とおくと,
T(s) = 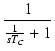
|
(145) |
となります.
右側のLRによるハイパスフィルタの伝達関数は,
L/R = TL とおくと,
T(s) = 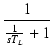
|
(147) |
となり,CRの場合と同じ形になりました.
一般に,1次のハイパス特性の伝達関数は,
T(s) = 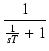
|
(148) |
となり,p = - 1/T とおけば,
T(s) = 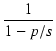
|
(149) |
となります.
この伝達関数,のゲインと位相の周波数特性を調べてみましょう.
そのために,
 = - p とおき,s = j
= - p とおき,s = j を代入し,有理化します.
を代入し,有理化します.
ゲインは,
となります.

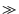
 のとき,
のとき,
 /
/
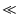 1 となり,分母はほぼ 1 ですので,
| T|
1 となり,分母はほぼ 1 ですので,
| T| 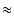 1 となります.
1 となります.
 =
=  のとき,分母は
のとき,分母は 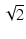 となるので,
| T| = 1/
となるので,
| T| = 1/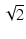 となります.
これをデシベルで表すと約 -3 dB です.
となります.
これをデシベルで表すと約 -3 dB です.

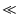
 のとき,
のとき,
 /
/
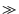 1 となり,分母の根号の中の 1 を無視することができるので,
| T|
1 となり,分母の根号の中の 1 を無視することができるので,
| T| 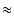 1/(
1/( /
/ ) =
) =  /
/ となります.
したがって,周波数が1/10となるごとにゲインは1/10になり,
-20 dB/dec または
-6 dB/oct でゲインが直線的に下がります.
となります.
したがって,周波数が1/10となるごとにゲインは1/10になり,
-20 dB/dec または
-6 dB/oct でゲインが直線的に下がります.
位相は,
arg T(j ) ) |
= |
tan-1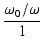 = tan-1 = tan-1 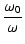 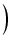 |
(152) |
となり,

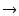 0 で 90o,
0 で 90o,
 =
=  で 45o,
で 45o,

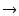
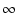 で 0o となります.
で 0o となります.
グラフで表すと,図38のようになります.
現実の回路では,無限にゲインが上昇する回路はあり得ないのですが,
解析に便利なため,ある周波数からゲインが上昇していく伝達関数を考えます.
T(s) = 1 - 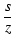
|
(153) |
z は,この伝達関数のゼロ(zero)で,
s = z のとき,伝達関数が0になります.
実際には,z は複素数ではないので,
この伝達関数の値が0になることはありません.
 = - z とおき,s に j
= - z とおき,s に j を代入すると,
を代入すると,
T(j ) = 1 + ) = 1 + 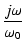
|
(154) |
となります.
一般に,伝達関数の分子 N(s) が0となる解をゼロといいいます.
伝達関数の分母の多項式は,ゼロ
z1, z2,... によって,次のように変形できます.
| N(s) |
= |
1 + a1s + a2s2 + a3s3 + ... |
(155) |
| |
= |
(1 - s/z1)(1 - s/z2)(1 - s/z3) ... |
(156) |
これより,ゲインは,
| T(j )| = )| = 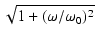
|
(157) |
となります.
したがって,

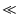
 のとき,
のとき,
 /
/
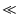 1 ですから,ゲインは
| T|
1 ですから,ゲインは
| T| 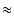 1 となります.
1 となります.
 =
=  のとき,
| T| =
のとき,
| T| = 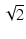 となり,これは約 +3 dB です.
となり,これは約 +3 dB です.

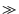
 のとき,
のとき,
 /
/
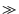 1 ですから,根号の中の1を無視できて,ゲインは
| T|
1 ですから,根号の中の1を無視できて,ゲインは
| T| 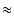
 /
/ となり,周波数が10倍になればゲインも10倍になります.
となり,周波数が10倍になればゲインも10倍になります.
位相は,
arg T(j ) = tan-1 ) = tan-1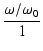 = tan-1 = tan-1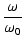
|
(158) |
で,

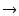 0 のとき 0o,
0 のとき 0o,
 =
=  のとき 45o,
のとき 45o,

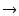
 のとき 90o となります.
のとき 90o となります.
グラフで表すと,図39のようになります.
ある周波数以下でゲインが上昇していく伝達関数を考えます.
T(s) = 1 - 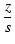
|
(159) |
 = - z とおき,s に j
= - z とおき,s に j を代入すると,
となります.
を代入すると,
となります.
これより,ゲインは,
| T(j )| = )| = 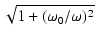
|
(161) |
となります.
したがって,

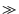
 のとき,
のとき,
 /
/
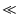 1 ですから,ゲインは
| T|
1 ですから,ゲインは
| T| 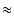 1 となります.
1 となります.
 =
=  のとき,
| T| =
のとき,
| T| = 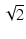 となり,これは約 +3 dB です.
となり,これは約 +3 dB です.

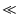
 のとき,
のとき,
 /
/
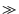 1 ですから,根号の中の1を無視できて,ゲインは
| T|
1 ですから,根号の中の1を無視できて,ゲインは
| T| 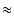
 /
/ となり,周波数が1/10倍になればゲインは10倍になります.
となり,周波数が1/10倍になればゲインは10倍になります.
位相は,
arg T(j ) = tan-1 ) = tan-1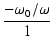 = tan-1 = tan-1 - - 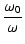 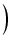
|
(162) |
で,

 0 のとき -90o,
0 のとき -90o,
 =
=  のとき -45o,
のとき -45o,

 のとき 0o となります.
のとき 0o となります.
グラフで表すと,図40のようになります.
伝達関数は,式(109)より,
T(s) =  . . 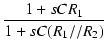
|
(163) |
で,
| z |
= |
- 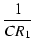 |
(164) |
| p |
= |
- 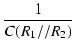 |
(165) |
とおけば,
T(s) =  . . 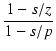 = =  . (1 - s/z) . . (1 - s/z) . 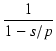
|
(166) |
と書けます.
この式の第1項は,周波数に依存しません.
第2項はハイブースト特性で,| z| より周波数が高くなるとゲインが上昇します.
第3項はハイカット(ローパス)特性で,| p| より周波数が高くなるとゲインが下降します.
伝達関数の積は,ゲインに関してはそれぞれの積に,位相に関しては和になります.
ゲインをデシベルで表した場合は,ゲインも和になります.
この場合,
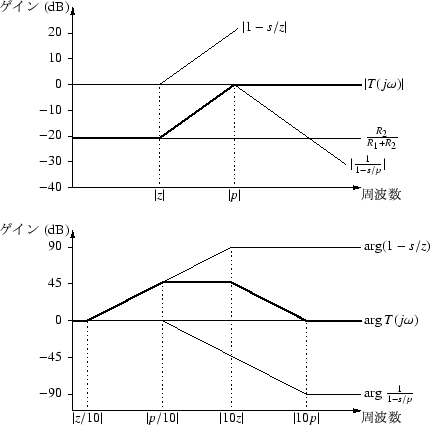
R1 > (R1//R2) なので,| z| < | p| となります.
したがってゲインの周波数特性は,低域では
R2/(R1 + R2) で,
| z| からゲインが
6 dB/oct で上昇し,| p| で平坦に戻ります.
このようすを漸近線で示したものが,図41です.
図 41:
微分型位相補償の特性(漸近線による)
 |
ゼロ,ポールの値は,
| z |
= |
- 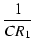 = - = - 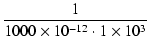 = - 1 x 106 [rad /s] = - 159 [kHz] = - 1 x 106 [rad /s] = - 159 [kHz] |
(167) |
| p |
= |
- 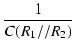 = - = - 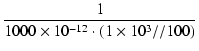 = - 11 x 106 [rad /s] = - 1.75 [MHz] = - 11 x 106 [rad /s] = - 1.75 [MHz] |
(168) |
です.
位相は,
となります.
位相がもっとも進むのは,証明は省略しますが
 =
= 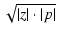 の時で,
このときの角周波数を
の時で,
このときの角周波数を 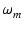 とすると,
とすると,
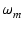 = = 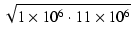 = 3.3 x 106 [rad /s] = 525 [kHz] = 3.3 x 106 [rad /s] = 525 [kHz]
|
(170) |
なので,
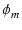 = tan-13.3 - tan-1 = tan-13.3 - tan-1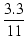 = 56.4 [o] = 56.4 [o]
|
(171) |
となります.
特性を図42に示します.
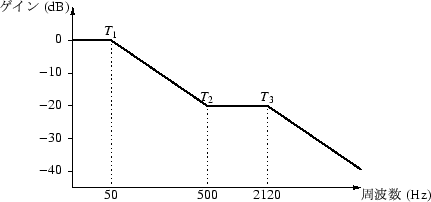
RIAAイコライザの特性は,図43のようになっており,
時定数は,
| T1 |
= |
3180 [μs] |
|
| T2 |
= |
318 [μs] |
|
| T3 |
= |
75 [μs] |
|
と定められています.
この特性を実現する伝達関数は,
T(s) = A0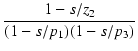
|
(172) |
のようになります.
ここで,
| p1 |
= |
- 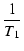 = - 314.5 [rad /s] = - 50 [Hz] = - 314.5 [rad /s] = - 50 [Hz] |
|
| z2 |
= |
- 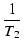 = - 3145 [rad /s] = - 500 [Hz] = - 3145 [rad /s] = - 500 [Hz] |
|
| p3 |
= |
- 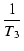 = - 13333 [rad /s] = - 2120 [Hz] = - 13333 [rad /s] = - 2120 [Hz] |
|
です.
図 43:
RIAAイコライジング特性
 |
この特性を実現するには,たとえば図44のような回路を使います.
図 44:
CR型RIAAイコライザ
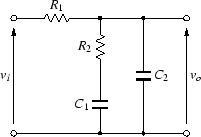 |
この回路の伝達関数を求めます.
R2, C1, C2 の部分のインピーダンスを Z とおくと,
| Z |
= |
(R2 + ZC1)//ZC2 |
|
| |
= |
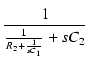 |
|
| |
= |
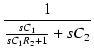 |
|
| |
= |
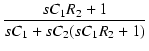 |
|
| |
= |
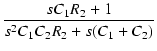 |
|
これを使うと,この回路の伝達関数は,
となります.
一方,式(172)より,
ですから,s の各係数を比較することにより,
| C1R2 |
= |
T2 |
(175) |
| C1C2R1R2 |
= |
T1T3 |
(176) |
| C1R1 + C1R2 + C2R1 |
= |
T1 + T3 |
(177) |
という関係が成り立つことがわかります.
式(175)を式(176)に代入することにより,
| C2R1T2 |
= |
T1T3 |
|
| C2R1 |
= |
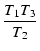 |
(178) |
これらを式(177)に代入することにより,
C1R1 + T2 + 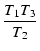 |
= |
T1 + T3 |
|
| C1R1 |
= |
T1 + T3 - T2 - 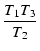 |
(179) |
となります.
まとめると,
| C1R2 |
= |
T2 = 318 [μs] |
(180) |
| C2R1 |
= |
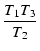 = 750 [μs] = 750 [μs] |
(181) |
| C1R1 |
= |
T1 + T3 - T2 - 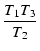 = 2187 [μs] = 2187 [μs] |
(182) |
を満たす定数をもとめればよいことになります.
C1 としてE6系列の
0.047 μF を選ぶと,
| R2 |
= |
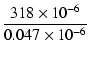  6.8 [kΩ] 6.8 [kΩ] |
|
| R1 |
= |
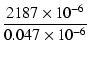 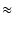 47 [kΩ] 47 [kΩ] |
|
| C2 |
= |
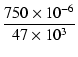 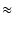 0.016 [μF] 0.016 [μF] |
|
となります.
C2 としては,
0.015 μF と
0.001 μF を並列にすればよいでしょう.
この回路の特性とRIAA偏差を調べましょう.
function ()
{
f <- dec(10, 100e3, 30) # 周波数
s <- (0+1i) * 2 * pi * f
# 正しいRIAA特性
T1 <- 3180e-6
T2 <- 318e-6
T3 <- 75e-6
TT <- (1+s*T2)/((1+s*T1)*(1+s*T3))
# 容易に入手可能な定数によるRIAA特性
R1 <- 47e3
R2 <- 6.8e3
C1 <- 0.047e-6
C2 <- 0.016e-6
T <- (1+s*C1*R2)/(1 + s*(C1*R1+C1*R2+C2*R1) + s^2*C1*C2*R1*R2)
# 次段の入力インピーダンスが1Mohmの場合の特性
Z <- (R2 + 1/(s*C1)) %p% (1/(s*C2)) %p% 1e6
Tp <- Z / (R1 + Z)
par(mfrow=c(2, 1))
semilogplot(f, dB(cbind(T, Tp)), type="l", lty=1, col=c("red", "blue"),
xlim=c(20, 20e3), ylim=c(-40, 0), yaxs="i",
xlab="Frequency (Hz)", ylab="Gain (dB)")
d <- T / TT # RIAA偏差
d <- d / d[near(f, 1e3)] # 偏差の基準を1kHzにする
dp <- Tp / TT # RIAA偏差(次段のZin=1Mohm)
dp <- dp / dp[near(f, 1e3)]
semilogplot(f, dB(cbind(d, dp)), type="l", lty=1, col=c("red", "blue"),
xlim=c(20, 20e3), ylim=c(-1, 1), yaxs="i",
xlab="Frequency (Hz)", ylab="RIAA error (dB)")
}
関数 near(x, v) は,値 v にもっとも近い配列 x の要素の番号(添字)を返します.
したがって,d[near(f, 1e3)] は,1kHz にもっとも近い周波数のRIAA偏差の値になります.
この値ですべてのRIAA偏差を割っていますから,1kHz の偏差が 1 (0dB)になります.
赤い線は次段の入力インピーダンスが無限大の場合で,
青い線は次段の入力インピーダンスが 1 MΩ の場合です.
このように,次段の入力インピーダンスが低くなると,
低域のRIAA偏差がマイナス方向に大きくなります.
この偏差を小さくするには,最初から次段の入力インピーダンスを含めて伝達関数を求めます.
図47 (a)では,次段の入力インピーダンスとして R3 を含めました.
図 47:
CR型RIAAイコライザに次段の入力インピーダンスを付加
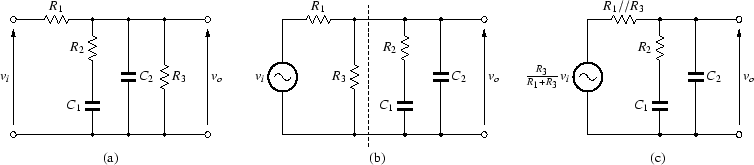 |
この R3 を(b)のように R1 の直後に移します.
点線から左側を見たインピーダンスは R1//R3 であり,
この点線で切り離した時の開放電圧は
viR3/(R1 + R3) ですから,
テブナンの定理により,(c)のように書き直せます.
したがって,R1//R3 が
47 kΩ になるようにすれば,
RIAA特性が得られます.
たとえば,
R3 = 470 kΩ とすると,R1 の値は,
R1 = 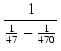 = 52.2 [kΩ] = 52.2 [kΩ]
|
(183) |
ですから,
51 kΩ を使えばよいでしょう.
R1 = 51 kΩ,
R3 = 470 kΩ とした場合のRIAA特性と,
偏差をグラフに描きましょう.

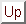

Next: 7 伝達関数 2次の場合
Up: オーディオのための交流理論入門
Previous: 5 複素数
Ayumi Nakabayashi
平成19年12月8日
![]() を使ってきましたが,
これからは,これを s で表します.
今回は扱いませんが,この s はラプラス変数で,
ラプラス変換を使えば過渡応答を求めることもできます.
正弦波に対する定常的な応答を求めるには,s に j
を使ってきましたが,
これからは,これを s で表します.
今回は扱いませんが,この s はラプラス変数で,
ラプラス変換を使えば過渡応答を求めることもできます.
正弦波に対する定常的な応答を求めるには,s に j![]() を代入してやります.
を代入してやります.
 =
= 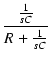 =
= 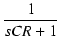
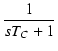
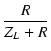 =
= 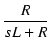 =
= 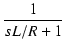
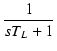
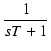
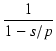
![]() = - p とおき,s = j
= - p とおき,s = j![]() を代入し,有理化します.
を代入し,有理化します.
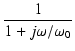 =
= 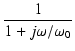 .
. 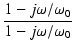
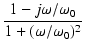
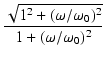 =
= 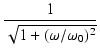
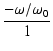 = tan-1
= tan-1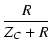 =
= 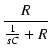 =
= 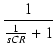
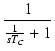
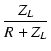 =
= 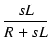 =
= 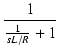
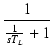
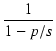
![]() = - p とおき,s = j
= - p とおき,s = j![]() を代入し,有理化します.
を代入し,有理化します.
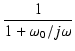 =
= 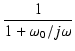 .
. 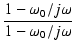
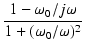 =
= 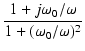
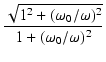 =
= 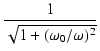
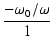 = tan-1
= tan-1 .
. 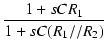
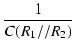
 .
. 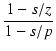 =
=  . (1 - s/z) .
. (1 - s/z) . 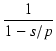
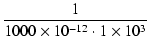 = - 1 x 106 [rad /s] = - 159 [kHz]
= - 1 x 106 [rad /s] = - 159 [kHz]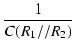 = -
= - 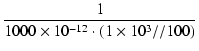 = - 11 x 106 [rad /s] = - 1.75 [MHz]
= - 11 x 106 [rad /s] = - 1.75 [MHz]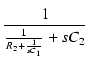
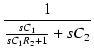
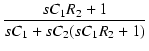
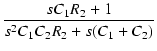
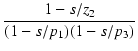 =
= 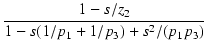 =
= 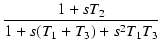
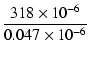
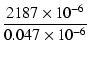
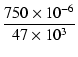
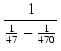 = 52.2 [kΩ]
= 52.2 [kΩ]