Next: A. 公式 Up: オーディオのための交流理論入門 Previous: 10 位相補償

11 出力段の位相補償

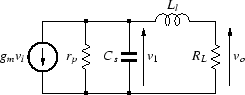
この節では，出力トランスの一次側や二次側に位相補償用の素子を付加した回路の特性を調べます．出力トランスの等価回路は，そのままでは複雑になるので，浮遊容量などをすべて一次側に集めて解析をしていくので，実際の特性とは少し異なりますので，その点をご了承願います．

11.1 出力段の特性

出力トランス付きの出力段の等価回路は，図133のように表せます．ここで，

g_m	=	出力デバイスの相互コンダクタンス
r_p	=	出力デバイスの出力(内部)抵抗
L_l	=	出力トランスの漏れインダクタンス
C_s	=	出力トランスの一次換算浮遊容量
R_L	=	一次換算負荷

**図 133:** 出力段の等価回路
$\begin{figure}\input{figs/pow_eqv} \end{figure}$

出力段の伝達関数を求めます．

v₁	=	- g_mv_i[r_p//Z_{C_s}//(Z_{L_l} + R_L)]
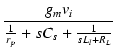	=	- $\displaystyle {\frac{{g_m v_i}}{{\frac{1}{r_p} + sC_s + \frac{1}{sL_l + R_L}}}}$
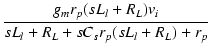	=	- $\displaystyle {\frac{{g_m r_p (sL_l + R_L) v_i}}{{sL_l + R_L + sC_s r_p (sL_l + R_L) + r_p}}}$
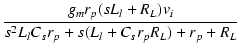	=	- $\displaystyle {\frac{{g_m r_p (sL_l + R_L) v_i}}{{s^2 L_l C_s r_p + s(L_l + C_s r_p R_L) + r_p + R_L}}}$
v_o	=	v₁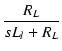 $\displaystyle {\frac{{R_L}}{{sL_l + R_L}}}$
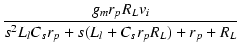	=	- $\displaystyle {\frac{{g_m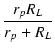 r_p R_L v_i}}{{s^2 L_l C_s r_p + s(L_l + C_s r_p R_L) + r_p + R_L}}}$
	=	- g_m $\displaystyle {\frac{{r_p R_L}}{{r_p + R_L}}}$ v_i^. $\displaystyle {\frac{{1}}{{s^2 \frac{L_l C_s r_p}{r_p + R_L} + s[\frac{L_l}{r_p + R_L} + C_s (r_p // R_L)] + 1}}}$
A(s)	=	- g_m(r_p//R_L)^. $\displaystyle {\frac{{1}}{{s^2 \frac{L_l C_s r_p}{r_p + R_L} + s[\frac{L_l}{r_p + R_L} + C_s (r_p // R_L)] + 1}}}$

低域のゲインを A₀ = - g_m(r_p//R_L) とおけば，

A(s) = A₀^. $\displaystyle {\frac{{1}}{{s^2 \frac{L_l C_s r_p}{r_p + R_L} + s[\frac{L_l}{r_p + R_L} + C_s (r_p // R_L)] + 1}}}$

(374)

この回路の固有振動周波数 w₀ と Q は，

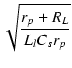w₀	=	$\displaystyle \sqrt{{\frac{r_p + R_L}{L_l C_s r_p}}}$	(375)
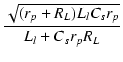Q	=	$\displaystyle {\frac{{\sqrt{(r_p+R_L)L_l C_s r_p}}}{{L_l + C_s r_p R_L}}}$	(376)

11.2 1次側の位相補償

出力トランスの1次側で積分型の位相補償を行なった場合の等価回路は，図134のように表せます．

**図 134:** 出力トランスの1次側の位相補償
$\begin{figure}\input{figs/pow_pc1} \end{figure}$

出力段の伝達関数を求めます．

v₁	=	- g_mv_i[r_p//(R_c + Z_{C_c})//Z_{C_s}//(Z_{L_l} + R_L)]
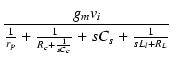	=	- $\displaystyle {\frac{{g_m v_i}}{{\frac{1}{r_p} + \frac{1}{R_c + \frac{1}{sC_c}} + sC_s + \frac{1}{sL_l + R_L}}}}$
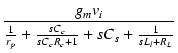	=	- $\displaystyle {\frac{{g_m v_i}}{{\frac{1}{r_p} + \frac{sC_c}{sC_cR_c + 1} + sC_s + \frac{1}{sL_l + R_L}}}}$
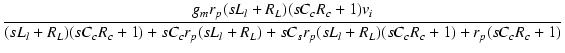	=	- $\displaystyle {\frac{{g_m r_p (sL_l+R_L)(sC_cR_c+1) v_i}}{{(sL_l + R_L)(sC_cR_c+1) + sC_cr_p(sL_l+R_L) + sC_s r_p (sL_l + R_L)(sC_cR_c+1) + r_p(sC_cR_c+1)}}}$
	=	- $\displaystyle {\frac{{g_m r_p (sL_l+R_L)(sC_cR_c+1) v_i}}{{s^3 L_lC_cC_sr_pR_c ... ...C_cC_sr_pR_cR_L\} + s[L_l+C_sr_pR_L + C_c(r_pR_L+r_pR_c+R_cR_L)] + r_p + R_L}}}$
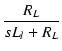v_o	=	v₁ $\displaystyle {\frac{{R_L}}{{sL_l + R_L}}}$
	=	- $\displaystyle {\frac{{g_m r_p R_L (sC_cR_c+1) v_i}}{{s^3 L_lC_cC_sr_pR_c + s^2\... ...C_cC_sr_pR_cR_L\} + s[L_l+C_sr_pR_L + C_c(r_pR_L+r_pR_c+R_cR_L)] + r_p + R_L}}}$
	=	- g_m(r_p//R_L)v_i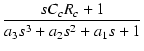^. $\displaystyle {\frac{{sC_cR_c+1}}{{a_3 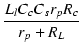s^3 + a_2 s^2 + a_1 s + 1}}}$

ここで，

a₃	=	$\displaystyle {\frac{{L_lC_cC_sr_pR_c}}{{r_p+R_L}}}$
a₂	=	$\displaystyle {\frac{{L_l[C_sr_p + C_c(r_p + R_c)] + C_cC_sr_pR_cR_L}}{{r_p+R_L}}}$
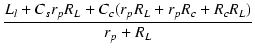a₁	=	$\displaystyle {\frac{{L_l+C_sr_pR_L + C_c(r_pR_L+r_pR_c+R_cR_L)}}{{r_p+R_L}}}$

です．

11.2.1 数値例

ここでは，例として，次のパラメータのトランスを使った出力段の位相補償を行います．

L_l	=	42.3 mH
C_s	=	284 pF
R_L	=	5 kΩ

出力管の内部抵抗は， 1.35 kΩ (三極管)または 23 kΩ (五極管)とします．

補償用抵抗として， 2.5 kΩ, 5 kΩ, 10 kΩ を使った場合に，補償用容量を変化させたときのポールとゼロの値を，図135に示します．

**図 135:** OPT 1次側の位相補償のポールとゼロ
$\includegraphics{figs/optpc1_1.ps}$

プログラムは，以下のようになります．

function ()
{
    # OPT1次側による位相補償

    Ll <- 42.3e-3               # 漏れインダクタンス
    Cs <- 284e-12               # 浮遊容量
    RL <- 5e3                   # 負荷抵抗
    rp <- c(1.35e3, 23e3)       # 内部抵抗
    Rc <- c(2.5e3, 5e3, 10e3)       # 補償抵抗
    Cc <- dec(0.1, 10, 20) * 1e-9   # 補償容量
    par(mfrow=c(2, 3))
    for (k in seq(along=rp)) {
        for (i in seq(along=Rc)) {
            z <- matrix(NA, length(Cc), 4,      # ポールとゼロを格納する領域
                    dimnames=list(Cc, c("p1", "p2", "p3", "z")))
            for (j in seq(along=Cc)) {
                pz <- optpc1(rp=rp[k], Ll=Ll, Cs=Cs, RL=RL, Rc=Rc[i], Cc=Cc[j])
                z[j, 1:3] <- pz$p
                z[j, 4] <- pz$z
            }
            logplot(Cc*1e9, abs(z)/2/pi,
                type="l", col=c(rep("red", 3), "blue"), lty=1,
                xlab="Cc (nF)", ylab="p, z (Hz)",
                ylim=c(2e3, 1e6),
                main=paste("rp=", eunit(rp[k]), ", Rc=", eunit(Rc[i]), sep=""))
        }
    }
}

関数 optpc1 は， OPTの1次側で位相補償をした場合のポールとゼロを求める関数で，内容は以下のとおりです．

function(rp, Cs, Ll, RL, Rc, Cc) 
{
    a3 <- Ll * Cc * Cs * rp * Rc
    a2 <- Ll * (Cs * rp + Cc * (rp + Rc)) + Cc * Cs * rp * Rc * RL
    a1 <- Ll + Cs * rp * RL + Cc * (rp * RL + rp * Rc + Rc * RL)
    a0 <- rp + RL
    p <- tri(a3, a2, a1, a0)    # ポールは3次方程式の解
    o <- order(abs(p))          # ポールの絶対値の大きさ順
    z <- -1/(Cc * Rc)
    list(p=p[o], z=z)
}

関数 tri は3次方程式の解を求める関数です．

赤い線はポールの周波数，青い線はゼロの周波数です．赤い線は，3本あるはずですが，2つの線がくっついているところもあります．この場合，分母多項式の解は複素数になります．スタガ比がもっとも大きくなるのは， 2番目のポールの周波数とゼロの周波数を等しい場合です．この場合のスタガ比は，

$\displaystyle \alpha{^\prime}$ = $\displaystyle {\frac{{p_3}}{{p_1}}}$

となります．

ある補償容量に対して，p₂ = z となる補償抵抗を求めてグラフに表したのが，図136です．

**図 136:** OPT 1次側の位相補償の最適補償容量と補償抵抗
$\includegraphics{figs/optpc1_2.ps}$

このグラフを描く関数は，以下のようになります．

function ()
{
    # OPT1次側による位相補償

    rp <- c(1.35e3, 23e3)       # 内部抵抗
    Ll <- 42.3e-3               # 漏れインダクタンス
    Cs <- 284e-12               # 浮遊容量
    RL <- 5e3                   # 負荷抵抗
    Cc <- dec(0.2, 5.1, 30) * 1e-9  # 補償容量
    par(mfrow=c(2, 3))
    for (j in seq(along=rp)) {
        z <- matrix(NA, length(Cc), 4,  # 各補償容量に対する最適な補償抵抗などを
            dimnames=list(Cc, c("Rc", "a", "p1", "p3")))    # 格納する領域
        for (i in seq(along=Cc)) {
            z[i, "Rc"] <- uniroot(function(Rc) {
                pz <- optpc1(rp=rp[j], Ll=Ll, Cs=Cs, RL=RL, Rc=Rc, Cc=Cc[i])
                abs(pz$p[2]) - abs(pz$z)    # 第2のポールとゼロが等しくなる
            }, c(100, 100e3))$root          # 補償抵抗を求める
            pz <- optpc1(rp=rp[j], Ll=Ll, Cs=Cs, RL=RL, Rc=z[i, "Rc"], Cc=Cc[i])
            z[i, "p1"] <- abs(pz$p[1])      # 最適な補償抵抗を使用した場合の p1
            z[i, "p3"] <- abs(pz$p[3])      # 最適な補償抵抗を使用した場合の p3
        }
        title <- paste("rp=", eunit(rp[j]), "\n", sep="")
        z[, "a"] <- z[, "p3"]/z[, "p1"]     # 補償後のスタガ比
        logplot(Cc*1e9, z[, "Rc"], type="l", col="red", main=title,
            xlab="Cc (nF)", ylab="Rc (ohm)", xlim=c(0.2, 5), ylim=c(1e3, 100e3))
        logplot(Cc*1e9, z[, "a"], type="l", col="red", main=title,
            xlab="Cc (nF)", ylab="a", xlim=c(0.2, 5), ylim=c(1, 100))
        logplot(Cc*1e9, z[, 3:4]/2/pi, type="l", col="red", lty=1, main=title,
            xlab="Cc (nF)", ylab="p (Hz)", xlim=c(0.2, 5), ylim=c(5e3, 500e3))
    }
}

関数の値が 0 になる変数の値を求める uniroot を使って，補償抵抗の値を探索しています．探索のための関数では，与えられた補償抵抗の候補値に対して， optpc1 を用いてポールとゼロの周波数を求め， | p₂| - | z| を返しています．

グラフからわかるように，内部抵抗が低い方がスタガ比を大きく稼げます．下のグラフでは C_c = 1600 pF あたりで線が曲がっていますが，これより補償容量が大きいと，実数の p₂ と z が等しくなり，これより補償容量が小さいと，複素数の p₂ (の絶対値)と z が等しくなります．

11.3 2次側の位相補償

出力トランスの2次側で積分型の位相補償を行なった場合の等価回路は，図137のように表せます．

**図 137:** 出力トランスの2次側の位相補償
$\begin{figure}\input{figs/pow_pc2} \end{figure}$

出力段の伝達関数を求めます．

Z_L	=	R_L//(R_c + Z_{C_c})
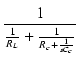	=	$\displaystyle {\frac{{1}}{{\frac{1}{R_L} + \frac{1}{R_c + \frac{1}{sC_c}}}}}$
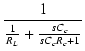	=	$\displaystyle {\frac{{1}}{{\frac{1}{R_L} + \frac{sC_c}{sC_cR_c + 1}}}}$
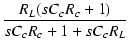	=	$\displaystyle {\frac{{R_L(sC_cR_c+1)}}{{sC_cR_c + 1 + sC_cR_L}}}$
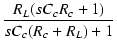	=	$\displaystyle {\frac{{R_L(sC_cR_c+1)}}{{sC_c(R_c+R_L)+1}}}$
v₁	=	- g_mv_i[r_p//Z_{C_s}//(Z_{L_l} + Z_L)]
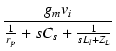	=	- $\displaystyle {\frac{{g_m v_i}}{{\frac{1}{r_p} + sC_s + \frac{1}{sL_l + Z_L}}}}$
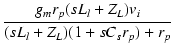	=	- $\displaystyle {\frac{{g_m r_p (sL_l + Z_L) v_i}}{{(sL_l + Z_L)(1 + sC_sr_p) + r_p}}}$
v_o	=	v₁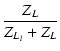 $\displaystyle {\frac{{Z_L}}{{Z_{L_l} + Z_L}}}$
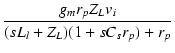	=	- $\displaystyle {\frac{{g_m r_p Z_L v_i}}{{(sL_l + Z_L)(1 + sC_sr_p) + r_p}}}$
	=	- $\displaystyle {\frac{{g_m r_p \frac{R_L(sC_cR_c+1)}{sC_c(R_c+R_L)+1} v_i}}{{[sL_l + \frac{R_L(sC_cR_c+1)}{sC_c(R_c+R_L)+1}](1 + sC_sr_p) + r_p}}}$
	=	- $\displaystyle {\frac{{g_m r_p R_L(sC_cR_c+1) v_i}}{{\{sL_l[sC_c(R_c+R_L)+1] + R_L(sC_cR_c+1)\}(1 + sC_sr_p) + r_p[sC_c(R_c+R_L)+1]}}}$
	=	- $\displaystyle {\frac{{g_m r_p R_L(sC_cR_c+1) v_i}}{{s^3 L_lC_cC_sr_p(R_c+R_L) +... ...p] + C_cC_sr_pR_cR_L\} + s\{L_l+C_sr_pR_L+C_c[r_pR_L+R_C(r_p+R_L)]\}+r_p+R_L}}}$
	=	- g_m(r_p//R_L)v_i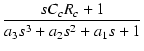^. $\displaystyle {\frac{{sC_cR_c+1}}{{a_3 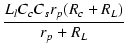s^3 + a_2 s^2 + a_1 s + 1}}}$

a₃	=	$\displaystyle {\frac{{L_lC_cC_sr_p(R_c+R_L)}}{{r_p+R_L}}}$
a₂	=	$\displaystyle {\frac{{L_l[C_c(R_c + R_L) + C_sr_p] + C_cC_sr_pR_cR_L}}{{r_p+R_L}}}$
a₁	=	$\displaystyle {\frac{{L_l+C_sr_pR_L+C_c[r_pR_L+R_C(r_p+R_L)]}}{{r_p+R_L}}}$

11.3.1 数値例

1次側の位相補償と同じ例を使います．プログラムは，optpc1 を optpc2 に変更するだけで使えます．関数 optpc2 は， OPTの2次側で位相補償をした場合のポールとゼロを求める関数で，内容は以下のとおりです．

function(rp, Cs, Ll, RL, Rc, Cc)
{
    a3 <- Ll * Cc * Cs * rp * (Rc + RL)
    a2 <- Ll * (Cc * (Rc + RL) + Cs * rp) + Cc * Cs * rp * Rc * RL
    a1 <- Ll + Cs * rp * RL + Cc * (rp * RL + Rc * (rp + RL))
    a0 <- rp + RL
    p <- tri(a3, a2, a1, a0)
    o <- order(abs(p))
    z <- -1/(Cc * Rc)
    list(p=p[o], z=z)
}

結果は，図138のようになります．

**図 138:** OPT 2次側の位相補償のポールとゼロ
$\includegraphics{figs/optpc2_1.ps}$

内部抵抗が高いと，p₃ が低くなって，ある程度以上の補償容量では p₂ と p₃ が共役の複素数になります．

ある補償容量に対して，p₂ = z となる補償抵抗を求めてグラフに表したのが，図139です．

**図 139:** OPT 2次側の位相補償の最適補償容量と補償抵抗
$\includegraphics{figs/optpc2_2.ps}$

グラフからわかるように，内部抵抗が高いと，ほとんどスタガ比が得られません．この補償方法は，三極管やウルトラリニア接続に向いているようです．

このグラフの補償容量，補償抵抗は，1次換算の値ですので，実際に2次側に入れる時は，インピーダンスの比だけ抵抗は小さく，容量は大きくします．たとえば，巻線比が 25 : 1 の場合は，抵抗は 1/625 に，コンデンサの容量は625倍にします．

Next: A. 公式 Up: オーディオのための交流理論入門 Previous: 10 位相補償

Ayumi Nakabayashi
平成19年12月8日