Next: 2 交流正弦波 Up: オーディオのための交流理論入門 Previous: はじめに

1 コンデンサ，コイル

ここでは，コンデンサ，コイルに加えた電圧と，流れる電流の関係を調べます．微分・積分の式が出てきますが，これは後で出てくる記号計算の根拠を示すためであって，実際の計算には使いません．

1.1 コンデンサ

図1のように，コンデンサに一定の電流を流すと，コンデンサの極板に電荷が溜まっていき，電極の電位差 v_C が大きくなっていきます．

**図 1:** コンデンサに一定の電流を流す
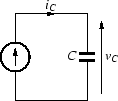
$\begin{figure}\input{figs/c_sch} \end{figure}$

このようすを，横軸に時間，縦軸に電位差をとってグラフで表すと，図2のようになります．これは，1 F のコンデンサに 1 A の電流を流した場合です．

**図 2:** コンデンサに一定の電流を流した場合の電圧の変化
$\begin{figure}\input{figs/c_tran} \end{figure}$

電流の大きさを変えてSPICEで検証してみましょう．シミュレーションの回路と結果は，図3のようになります． SPICEでは，コンデンサの値として 1F と指定すると，フェムトファラドとして解釈されてしまいますので，注意してください． .IC が付いているのは， SPICEの過渡解析における電圧の初期値を指定するものです．

**図 3:** コンデンサに一定の電流を流すシミュレーション
$\begin{figure}. % \end{figure}$

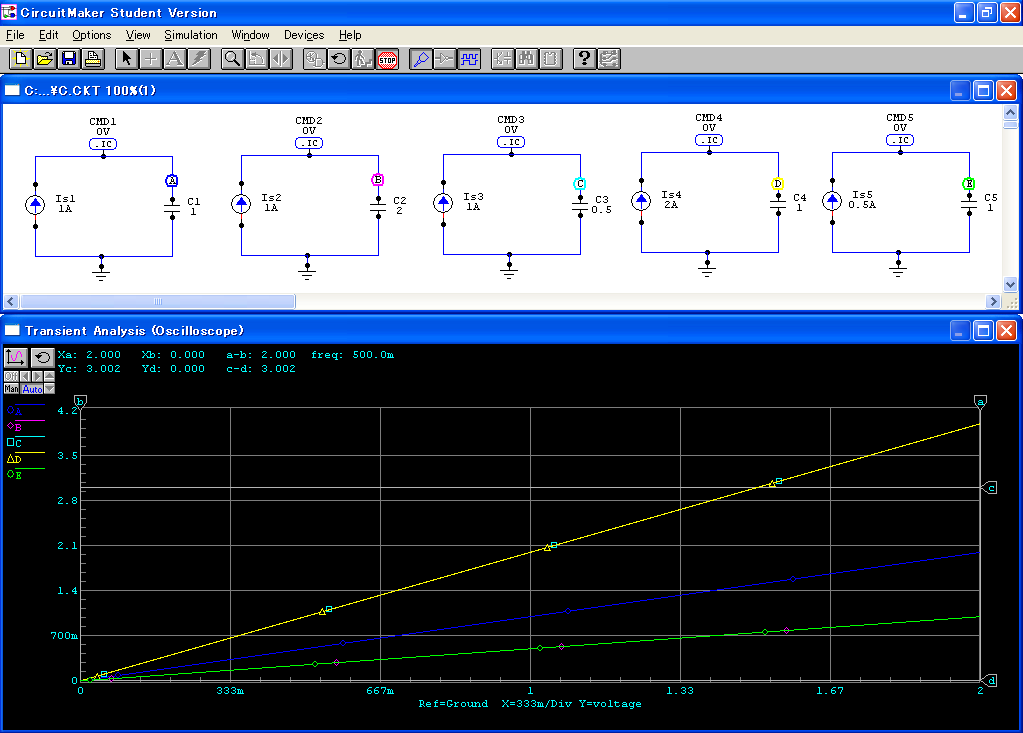
電流を増やす(図3のE, A, D)と，グラフの傾きが急になります．電流を時間で積分したものが，電極の電位差であるといえます．逆に，電極の電位差を時間で微分したものが，コンデンサを流れる電流といえます．式で表すと，

v_C	=	a $\displaystyle \int$ i_C dt	(1)
i_C	=	$\displaystyle {\frac{{1}}{{a}}}$ ^. $\displaystyle {\frac{{d v_C}}{{d t}}}$	(2)

となります．a は比例定数です．

次に，コンデンサの容量を変えてみます．コンデンサの容量が大きい(図3のC, A, B)と，同じ電流を流しても電位差の上昇スピードが低くなります．したがって，上述の式の比例定数 a は，コンデンサの容量 C に反比例します．つまり，コンデンサにかかる電圧と電流の関係は，次のようになります．

v_C	=	$\displaystyle {\frac{{1}}{{C}}}$ $\displaystyle \int$ i_C dt	(3)
i_C	=	C $\displaystyle {\frac{{d v_C}}{{d t}}}$	(4)

この式は，正弦波だけでなく，任意の電圧，電流に関して成り立つ基本的な関係です．

1.2 コイル

図4のように，コイルに一定の電圧をかけると，流れる電流は時間とともに増えていきます．

**図 4:** コイルに一定の電圧をかける
$\begin{figure}\input{figs/l_sch} \end{figure}$

このようすを，横軸に時間，縦軸に電流をとってグラフで表すと，図5のようになります．

**図 5:** コイルに一定の電圧をかけた場合の電流の変化
$\begin{figure}\input{figs/l_tran} \end{figure}$

これは，1 H のコイルに 1 V の電圧をかけた場合です．

電圧の大きさを変えてSPICEで検証してみましょう．シミュレーションの回路と結果は，図6のようになります． SPICEでは，電源とコイルを直結すると，直流では無限大の電流が流れてしまいますので，微少な抵抗(ここでは 1 μΩ)を入れます．

**図 6:** コイルに一定の電圧をかけるシミュレーション
$\begin{figure}. % \end{figure}$

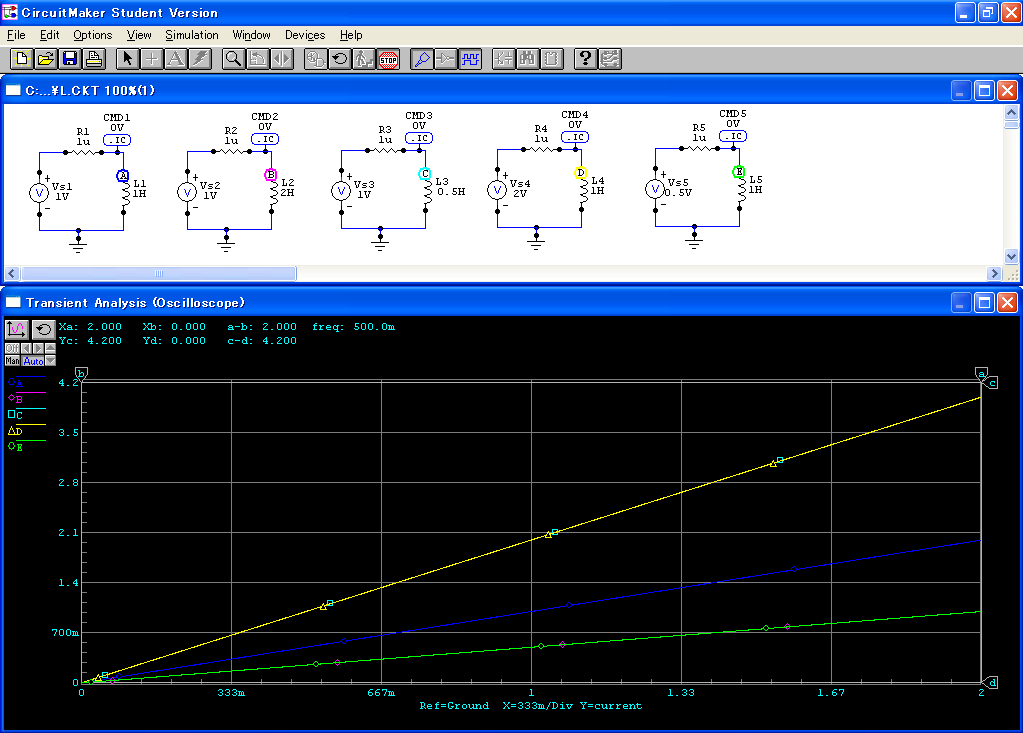
電圧を増やす(図6のE, A, C)と，グラフの傾きが急になります．電圧を時間で積分したものが，流れる電流であるといえます．逆に，コイルを流れる電流を時間で微分したものが，コイルの両端の電圧であるといえます．式で表すと，

i_L	=	b $\displaystyle \int$ v_L dt	(5)
v_L	=	$\displaystyle {\frac{{1}}{{b}}}$ ^. $\displaystyle {\frac{{d i_L}}{{dt}}}$	(6)

となります．b は比例定数です．

次に，コイルのインダクタンスを変えてみます．インダクタンスが大きい(図6のC, A, B)と，同じ電圧をかけても電流の上昇スピードが低くなります．したがって，上述の式の比例定数 b は，コイルのインダクタンス L に反比例します．つまり，コンデンサにかかる電圧と電流の関係は，次のようになります．

i_L	=	$\displaystyle {\frac{{1}}{{L}}}$ $\displaystyle \int$ v_L dt	(7)
v_L	=	L $\displaystyle {\frac{{d i_L}}{{dt}}}$	(8)

コンデンサの場合と同様に，この式は正弦波だけでなく，任意の電圧，電流に関して成り立つ基本的な関係です．

Next: 2 交流正弦波 Up: オーディオのための交流理論入門 Previous: はじめに

Ayumi Nakabayashi
平成19年12月8日