Next: 3 コンデンサ，コイルに正弦波を流すと Up: オーディオのための交流理論入門 Previous: 1 コンデンサ，コイル

2 交流--正弦波

交流解析では，単一の周波数の正弦波を扱います．ここでは，正弦波の正体をよく理解しておきましょう．

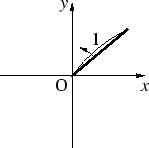
図7のように，x-y 平面の原点Oを中心として，その周りを長さが1の棒が一定の速度で反時計方向に回っている状態を考えてください．この棒の先から y 軸に垂線を下ろした点を縦軸に，横軸に時間の経過をとってプロットしていくと，正弦波になります(図8)．

**図 7:** 原点の周りを回転する棒
$\begin{figure}\input{figs/ac1} \end{figure}$

**図 8:** 正弦波の形成
$\begin{figure}\input{figs/ac2} \end{figure}$

このとき，この棒が回転する速さを，一秒間に回った回数で表したものが 周波数(frequency)で，f で表します．単位はヘルツ [Hz]です．また，一秒間に回った角度で表すこともでき， 角周波数(angular frequency)といい， $\omega$ で表します．角度の単位としてラジアン [rad]を使うのが数学的に便利ですので，角周波数の単位はラジアン毎秒 [rad/s]となります．角度は，x 軸を基準に，反時計方向を正とします．周波数と角周波数の関係は，1回転が 2 $\pi$ ラジアンなので，

$\displaystyle \omega$ = 2 $\displaystyle \pi$ f

(9)

となります．

また，棒が一回転するのにかかった時間を周期(period)といい， T で表します．単位は(秒) [s]です．棒が f 回転すると1秒ですので，一回転にかかる時間は，

T = $\displaystyle {\frac{{1}}{{f}}}$

(10)

となります．

この図では，棒の長さが1でしたので，生成された正弦波の最大値は1，最小値は -1 となります．電気では，任意の大きさの正弦波を扱いますので，棒の長さを電圧の場合なら V_m で表すことにします．この V_m を最大値(maximum value)または振幅(amplitude)といいます．

任意の瞬間の電圧や電流を瞬時値(instantaneous value)といい，小文字を使って v(t), i(t) のように表します． (t) を付けない場合もありますが，ここでは時間によって変わる値，すなわち t の関数であることを強調するため，(t) を付けています．一方，振幅 V_m, I_m は時間に依存しない定数です．時刻 t における棒の角度 $\theta$ は，

$\displaystyle \theta$ = $\displaystyle \omega$ t = 2 $\displaystyle \pi$ ft

(11)

で，これを位相(phase)といいます．瞬時値は，

v(t) = V_msin( $\displaystyle \omega$ t) = V_msin(2 $\displaystyle \pi$ ft)

(12)

で表すことができます．

正弦波が一つだけならこれでよいのですが，複数の正弦波を扱う場合は，同じ周波数でも，図9のようにズレた場合を扱う必要がでてきます．

**図 9:** 位相のずれた正弦波
$\begin{figure}\input{figs/ac3} \end{figure}$

このズレを角度で表したものが位相差です．位相差は相対的なものであり，どの正弦波を基準にするかは，任意に決めてよいのです．図9の場合， v₂ は v₁ より遅れている，あるいは，v₁ は v₂ より進んでいるといいます．

位相を含めて瞬時値を表すと，

v(t) = V_msin( $\displaystyle \omega$ t + $\displaystyle \phi$ )

(13)

となります．特に，この $\phi$ は，時刻0の棒の角度を表しており，初期位相ということもあります．

$\phi$ の符号がプラスの場合，この信号は，基準となる信号に対して進んでいるといい， $\phi$ の符号がマイナスの場合，この信号は，基準となる信号に対して遅れているといいます．

角周波数の単位は[rad/s]でしたが，位相差の単位としては，おもに度 [deg]が使われます．ラジアンが使われることもあります．

7.4 まとめ

正弦波は次の式で表されます．

v(t) = V_msin( $\displaystyle \omega$ t + $\displaystyle \phi$ )

(14)

v(t)	=	$\displaystyle \mbox{時刻 $t$\ における(電圧の)瞬時値}$
V_m	=	最大値または振幅
$\displaystyle \omega$	=	$\displaystyle \mbox{角周波数($=2\pi f$)}$
f	=	周波数
$\displaystyle \phi$	=	初期位相
$\displaystyle \omega$ t + $\displaystyle \phi$	=	位相

演習1

周波数が 50Hz で，初期位相が +45^o の，振幅が 5V の正弦波を，時刻が0から 40ms まで描け．

回答例1

Rを使って描きます． q1 という関数を作成することにします．コマンドウィンドウのプロンプト(>)に対して， fix(q1) と入力します．これは，q1 というオブジェクトをエディタで修正(なければ新規作成)するコマンドです．図10 のようなウィンドウが開くので，画面の内容が以下のようになるよう，入力していきます． # 以降はコメントですので，面倒なら入力しなくても構いません．

**図 10:** Rのオブジェクト編集ウィンドウ
$\begin{figure}. % \end{figure}$

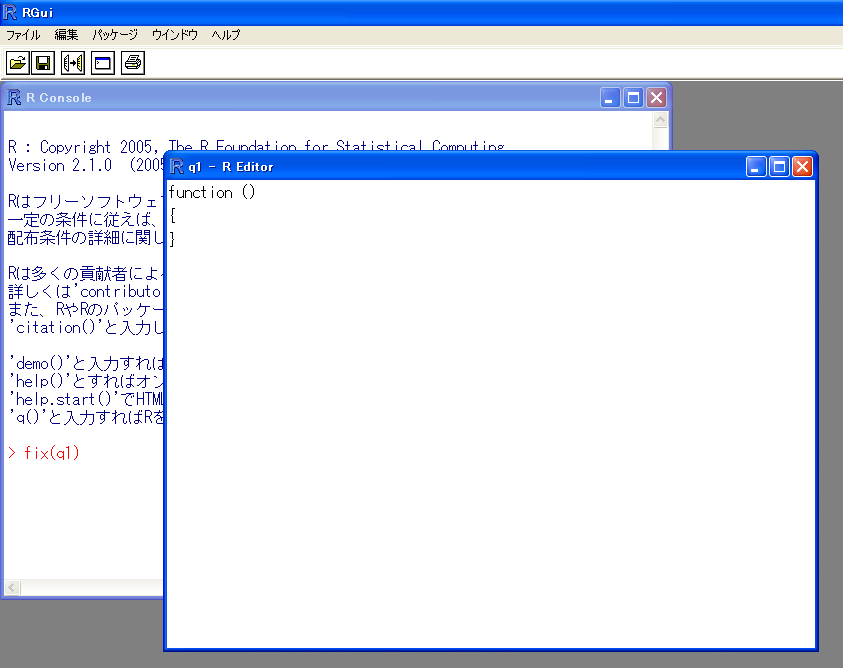
function ()
{
    t <- seq(0, 40e-3, len=200)         # 時刻(200点のベクトル)
    f <- 50                 # 周波数
    Vm <- 5                 # 振幅
    phi <- 45 * pi / 180    # 初期位相
    v <- Vm * sin(2 * pi * f * t + phi) # 瞬時値(200点)
    plot(t, v, type="l")    # グラフを描く
}

seq は等差数列を作成する関数，plot は xy 平面の2次元グラフを描く関数です．

入力が終わったら，ウィンドウを閉じるアイコンをクリックすると，内容を保存するかどうか尋ねてきますので， ``はい''を選択します．

今作成した関数の内容は，プロンプトに対して関数名を入力すると確認できます．

> q1
function ()
{
    t <- seq(0, 40e-3, len=200)         # 時刻(200点のベクトル)
    f <- 50                 # 周波数
    Vm <- 5                 # 振幅
    phi <- 45 / 180 * pi    # 初期位相
    v <- Vm * sin(2 * pi * f * t + phi) # 瞬時値(200点)
    plot(t, v, type="l")    # グラフを描く
}
>

関数を実行するには，引数を指定するかっこを付けます．今回の場合，引数がないので，かっこのみを後ろに付けます．

> q1()
>

グラフは別のウィンドウに表示されます．

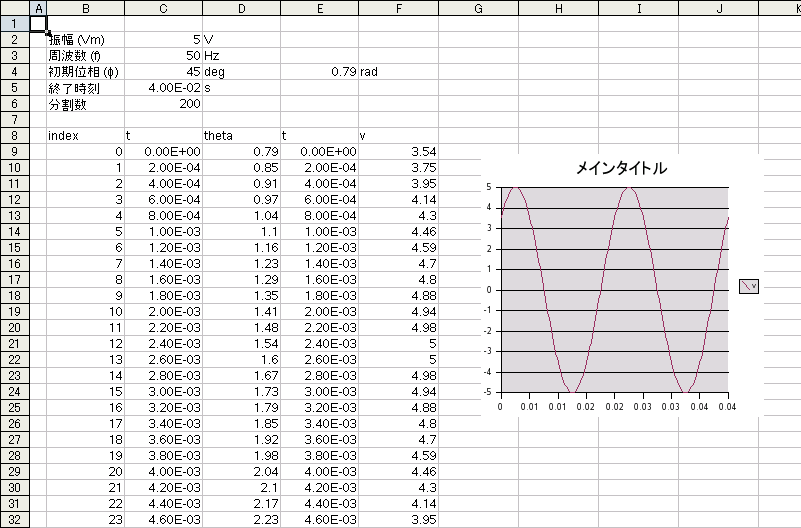
表計算ソフトでは，たとえば図11のようにすればよいでしょう．

**図 11:** 表計算ソフトで正弦波を描く
$\begin{figure}. % \end{figure}$

Next: 3 コンデンサ，コイルに正弦波を流すと Up: オーディオのための交流理論入門 Previous: 1 コンデンサ，コイル

Ayumi Nakabayashi
平成19年12月8日