Next: 4 複数の素子を組み合わせた場合 Up: オーディオのための交流理論入門 Previous: 2 交流正弦波

3 コンデンサ，コイルに正弦波を流すと

3.1 コンデンサに正弦波を流す

コンデンサに初期位相が0の正弦波を加えたときに流れる電流を計算します．式(4)に式(12)を代入すると，

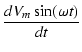i_C = C $\displaystyle {\frac{{d V_m \sin(\omega t)}}{{d t}}}$ = V_m $\displaystyle \omega$ C cos( $\displaystyle \omega$ t)

(15)

となります²．これは，振幅が V_m $\omega$ C の余弦波です．波形は，図12のようになります．

**図 12:** コンデンサに正弦波を加えたときの波形
$\begin{figure}\input{figs/c_iv} \end{figure}$

オームの法則と同様にして，抵抗値に相当するコンデンサのリアクタンス X_C を計算します．

X_C = $\displaystyle {\frac{{\vert v_C\vert}}{{\vert i_C\vert}}}$ = $\displaystyle {\frac{{V_m}}{{V_m \omega C}}}$ = $\displaystyle {\frac{{1}}{{\omega C}}}$ = $\displaystyle {\frac{{1}}{{2 \pi f C}}}$

(16)

となり，見慣れた式が出てきました．ちなみに，コンデンサの容量性リアクタンスの符号はマイナスなのですが，ここではとりあえず絶対値だけに注目しました．

余弦波は，時刻 0 で最大値をとり，これは正弦波が最大値をとる位相 90^o の時刻より 90^o 分先に進んでいるので，電流の位相は，電圧よりも 90^o 進んでいると言われます．

3.2 コイルに正弦波を流す

式(7)に式(12)を代入すると，

i_L = $\displaystyle {\frac{{1}}{{L}}}$ $\displaystyle \int$ V_msin( $\displaystyle \omega$ t) dt = - $\displaystyle {\frac{{V_m}}{{\omega L}}}$ cos( $\displaystyle \omega$ t)

(17)

となります．これは，振幅が V_m $\omega$ L の余弦波です(符号はマイナスです)．すなわち，電流の位相は，電圧よりも 90^o 遅れています．波形は，図13のようになります．

**図 13:** コイルに正弦波を加えたときの波形
$\begin{figure}\input{figs/l_iv} \end{figure}$

オームの法則と同様にして，抵抗値に相当するコイルのリアクタンス X_L を計算します．

X_L = $\displaystyle {\frac{{\vert v_C\vert}}{{\vert i_C\vert}}}$ = $\displaystyle {\frac{{V_m \omega L}}{{V_m}}}$ = $\displaystyle \omega$ L = 2 $\displaystyle \pi$ fL

(18)

となり，見慣れた式が出てきました．

3.3 SPICEによるシミュレーション

正弦波の電圧源に，コンデンサとコイルをそれぞれ接続し，流れる電流を測定します．回路と結果は，図14のようになります．

**図 14:** コンデンサ，コイルに正弦波を加える
$\begin{figure}. % \end{figure}$

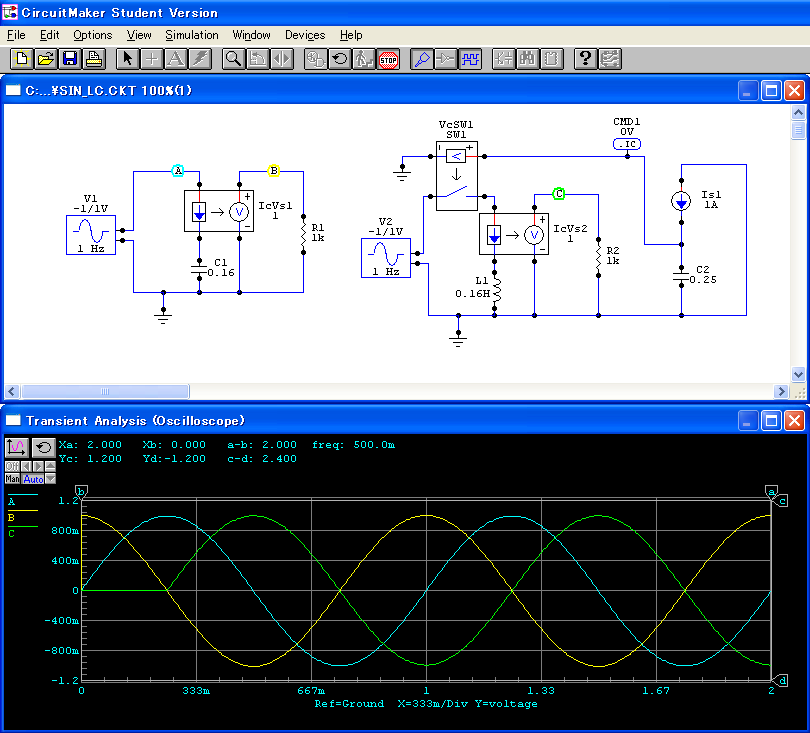
コンデンサに流れる電流を測定するのに，プローブをコンデンサの電流端子(?)に置けばよいように思われますが， CircuitMakerでこのようにすると，極性が逆になってしまうようです．そこで，電流制御電圧源 IcVs1 を使って，回路を流れている電流を電圧に変換し，電圧の値として取り出しています．変換の係数は1としていますから，1A の電流が 1V の電圧に変換されます．

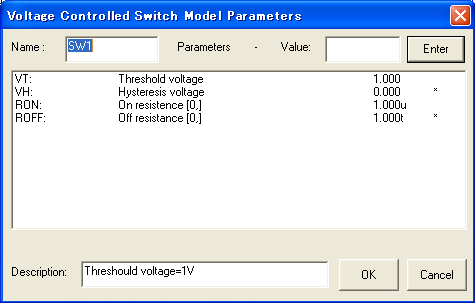
コイルのほうはさらにやっかいになっています．定常状態をいきなり作り出すために，電圧の最大値になったところで，回路を閉じて電流を流します．そのためのタイマーが C2 で， Is1 から一定の電流を流し，コンデンサの電圧が 1V になったらスイッチ VcSW1 が閉じます．電流は 1A, 容量が 0.25F なので，0.25秒後にスイッチが閉じます． VcSW1 のモデル SW1 は， 1V でスイッチが閉じ，そのときの抵抗は 1 μΩ となるように設定してあります(図15)．

**図 15:** スイッチのパラメータの設定
$\begin{figure}. % \end{figure}$

コンデンサを流れる電流(B)は，電圧(A)よりも位相が 90^o 進んでおり，コイルを流れる電流(C)は，電圧よりも位相が 90^o 遅れていることがわかります．

コイルのほうは，電圧源 V2 ではなく電流源を使えば，この例のようにスイッチを使う必要はありません．ぜひ試してみてください．その場合，回路の中にごく小さな抵抗を入れるのを忘れないでください．また，コイルの場合は，プローブの電流端子を使えるので， IcVs2 を使う必要はありません．また，この回路のままで，スイッチの部分を取り除いたらどのような波形になるか，試してみてください．

電流の大きさを計算してみましょう．コンデンサの容量は 0.16F ですから，1Hz におけるリアクタンス X_C は，

X_C = 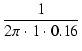$\displaystyle {\frac{{1}}{{2 \pi f C}}}$ = $\displaystyle {\frac{{1}}{{2\pi \cdot 1 \cdot 0.16}}}$ $\displaystyle \approx$ 1 [Ω]

(19)

したがって，電流(の振幅)は，

I_Cm = $\displaystyle {\frac{{V_m}}{{X_C}}}$ = $\displaystyle {\frac{{1}}{{1}}}$ = 1 [A]

(20)

となります．

同様に，コイルのインダクタンスは 0.16H ですから，1Hz におけるリアクタンス X_L は，

X_L = 2 $\displaystyle \pi$ fL = 2 $\displaystyle \pi$ ^.1^.0.16 $\displaystyle \approx$ 1 [Ω]

(21)

したがって，電流(の振幅)は，

I_Lm = $\displaystyle {\frac{{V_m}}{{X_L}}}$ = $\displaystyle {\frac{{1}}{{1}}}$ = 1 [A]

(22)

となります．

演習2

図14の例で，周波数を 2Hz にしたり，0.5Hz にしたときに，電流の大きさがどのようになるか予想し，シミュレーションで確かめましょう．

Next: 4 複数の素子を組み合わせた場合 Up: オーディオのための交流理論入門 Previous: 2 交流正弦波

Ayumi Nakabayashi
平成19年12月8日