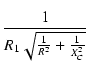 |
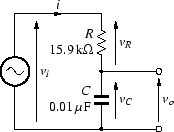
図16のように,抵抗 R とコンデンサ C を直列に接続し, 電圧 vi を加えます. このとき,コンデンサの両端を出力として,この電圧 vo = vC を求めます.
この回路はローパスフィルターです. 同じ入力電圧 vi を与えても, 周波数によって出力の大きさ(と位相)が変わってきます.
このように素子が直列に組み合わされている場合, 流れる電流は共通ですから,電流に着目して解析するのが簡単です. vi として何ボルトかけたのか不明ですが, この回路に振幅が 1mA の電流が流れたとしましょう. 周波数は 1kHz とします.
抵抗 R の両端には,オームの法則により,
| VRm = ImR = 1 x 10-3 . 15.9 x 103 = 15.9 [V] | (23) |
コンデンサ C の両端の電圧は, コンデンサのリアクタンス XC が
XC = 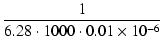 |
(24) |
| VCm = ImXC = 1 x 10-3 . 15.9 x 103 = 15.9 [V] | (25) |
この回路に加えられていた電圧の瞬時値 vi は, 抵抗の両端の電圧の瞬時値 vR と, コンデンサの両端の電圧の瞬時値 vC を加えたものになります.
| vi = vR + vC | (26) |
まずは,数値的に調べてみましょう. ここでは,Rを使います.
function ()
{
f <- 1e3 # 周波数
T <- 1/f # 周期
t <- seq(0, 2*T, len=201) # 2周期分
i <- 1e-3 * sin(2 * pi * f * t) # 電流の瞬時値
vR <- 15.9 * sin(2 * pi * f * t) # 抵抗の両端の電圧の瞬時値
vC <- -15.9 * cos(2 * pi * f * t) # コンデンサの両端の電圧の瞬時値
vi <- vR + vC # 入力電圧の瞬時値
par(mfrow=c(2, 1)) # グラフを2行1列にならべて描く
plot(t, i, type="l") # 電流の波形
matplot(t, cbind(vR, vC, vi), type="l", lty=1, col=2:4,
ylab="vR, vC, vi") # 電圧の波形
}
実行結果は,図18のようになります. 赤い線が抵抗の両端の電圧,緑の線がコンデンサの両端の電圧,青い線が入力電圧です.
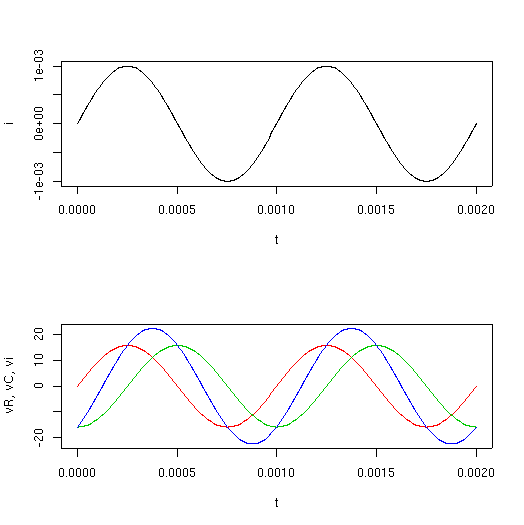
この結果を見ると, 入力電圧の振幅は 22.5V くらいに見えます. したがって,入力電圧を 1V とすれば, 出力電圧(コンデンサの両端の電圧)は 15.9/22.5 = 0.71 V くらいになります.
Rを使って,先ほどの関数を少し変えて, 周波数や抵抗などの値を変更しやすくします.
function(f=1e3, R=15.9e3, C=0.01e-6)
{
# f: 周波数(Hz)
# R: 抵抗値(ohm)
# C: 容量(F)
T <- 1/f # 周期
t <- seq(0, 2*T, len=201) # 2周期分
Im <- 1e-3 # 電流の振幅
VRm <- Im * R # 抵抗の両端の電圧の振幅
XC <- 1 / (2 * pi * f * C) # コンデンサのリアクタンス
VCm <- Im * XC # コンデンサの両端の電圧の振幅
cat("VRm=", VRm, "\n", sep="") # 表示
cat("XC=", XC, "\n", sep="")
cat("VCm=", VCm, "\n", sep="")
i <- Im * sin(2 * pi * f * t) # 電流の瞬時値
vR <- VRm * sin(2 * pi * f * t) # 抵抗の両端の電圧の瞬時値
vC <- -VCm * cos(2 * pi * f * t)# コンデンサの両端の電圧の瞬時値
vi <- vR + vC # 入力電圧の瞬時値
Vim <- max(vi) # 入力電圧の振幅
cat("Vim=", Vim, "\n", sep="")
cat("Vo/Vim=", VCm/Vim, "\n", sep="") # ゲイン
par(mfrow=c(2, 1)) # グラフを2行1列に並べて描く
plot(t, i, type="l") # 電流の波形
matplot(t, cbind(vR, vC, vi), type="l", lty=1, col=2:4,
ylab="vR, vC, vi") # 電圧の波形
}
function のかっこの中に書かれている変数は,
仮引数で,関数を実行する際に変更することができます.
= の後ろにある値は,引数が指定されなかった場合のデフォルトの値となります.
この関数を ac42 という名前で作成したとすると,
ac42(R=22e3) のように仮引数の名前(一部でよい)と値を指定してやれば,
その引数だけ値を変更できます.
指定しなかった引数は,デフォルトの値が使用されます.
> ac42(2e3) VRm=15.9 XC=7957.747 VCm=7.957747 Vim=17.77499 Vo/Vim=0.4476934 > windows() # もう一つグラフウィンドウを開く > ac42(500) VRm=15.9 XC=31830.99 VCm=31.83099 Vim=35.57143 Vo/Vim=0.894847
関数
windows() (Linuxの場合は X11())を使えば,
グラフウィンドウを追加で開くことができ,
複数のグラフを比較できます.
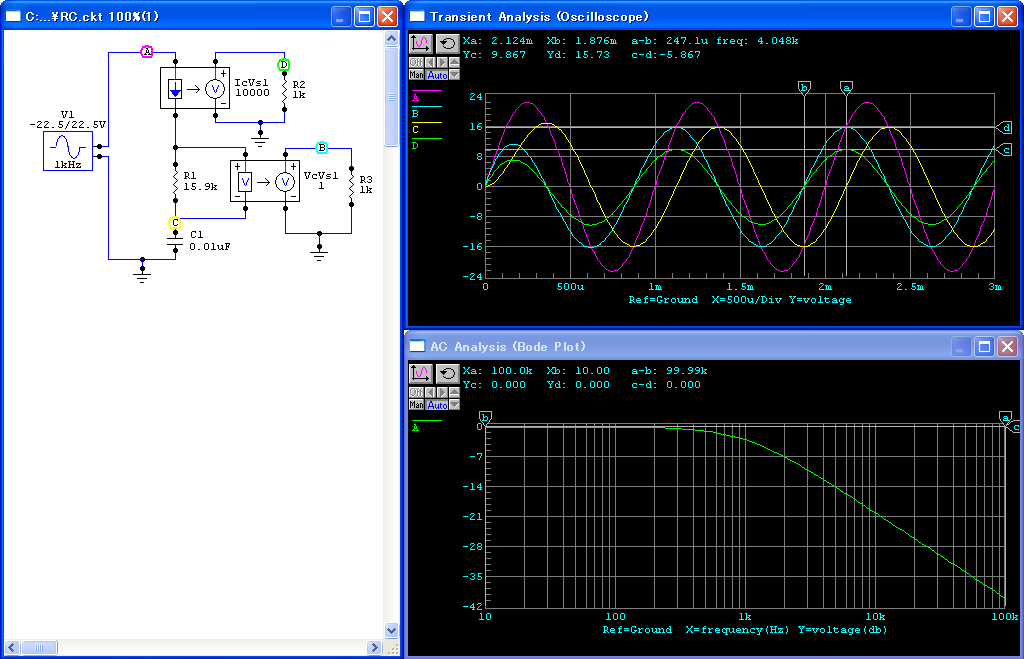
CircuitMakerでは,私が不慣れなせいかもしれませんが, 2点間の電圧のグラフを表示する方法がないようです.
VcVs1 を使って,2点間の電位差を対グラウンドの電圧に変換しています.
また念のため,回路を流れる電流は,IcVs1 で電圧に変換して取り出しています.
この係数として10000を指定しているので,1mA が 10V としてグラフに表示されます.
波形をみると,2周期目でほぼ定常状態になっているようです. 電流の波形(D)と抵抗の両端の電圧の波形(B)は位相が合っています. コンデンサの両端の波形(C)は,電流に比べて位相が 90o 遅れています. 入力電圧の波形(A)は,電流に比べて位相が 45o 遅れているようです. 振幅の関係は,Rで計算したものと同じになっています.
このように,瞬時値を使えば,この回路の入力電圧や出力電圧を求めることができますが, とても手間がかかります. 一度,三角関数の性質を使って,各部の電圧や電流の振幅や位相の関係を検討しておけば,簡単に計算することができるようになります. ただし,この節で説明した方法で実際の計算をすることもありません.
電流を基準にとり,その初期位相を0とすれば,電流の瞬時値は,
で表すことができます. 抵抗の両端の電圧の瞬時値は,オームの法則から,|
vR = iR = ImR sin( |
(28) |
|
vC = |
(29) |
ここで,正弦波と余弦波を任意の比率で足し合わせた波形がどうなるかを 見てみましょう.瞬時値 v を式で表すと,
となります. a, b は負であっても構いません.a を x 軸に,b を y 軸にとると,図20のような長方形ができます. 対角線OCの長さは,三平方の定理より,
|
OC = |
(32) |
|
tan |
(33) |
これらを使って a, b を表すと,
| a | = | ||
| b | = |
| v | = | a sin |
|
| = | |||
| = | |||
| = | (34) |
ここで,正弦波と余弦波を任意の比率で足し合わせた波形がどうなるかを, Rで確かめてみましょう. プログラムは少々長くなりますが,以下の通りです.
function (a=1, b=1)
{
# a: 正弦波の振幅
# b: 余弦波の振幅
th <- seq(-2*pi, 2*pi, len=201) # 位相
s <- a * sin(th) # 正弦波波形
c <- b * cos(th) # 余弦波波形
z <- s + c # 合成波波形
cat("max(z)=", max(z), "\n", sep="") # 合成波の振幅(波形から)
Vm <- sqrt(a^2 + b^2) # 合成波の振幅(解析的)
cat("Vm=", Vm, "\n", sep="")
phi <- atan2(b, a)*180/pi # 合成波の初期位相
cat("phi=", phi, "\n", sep="")
par(mfrow=c(2, 1)) # グラフを2行1列で描く
# 波形
matplot(th*180/pi, cbind(s, c, z), type="l", lty=1, col=2:4,
xaxs="i", xaxt="n",
xlab="Phase (deg)", ylab="Instantaneous value")
axis(1, at=seq(-360, 360, by=90), lab=FALSE, tck=1, col="gray")
axis(1, at=seq(-360, 360, by=90)) # 目盛を自分の好みで描く
box() # 周りが灰色になるのでワクを描き直す
abline(h=0) # 水平線を引く
abline(v=-phi, col=4) # 合成波の立ち上がり点
arrow(0, -Vm, -phi, -Vm, col=4)
text(-phi/2, -0.9*Vm, format(round(phi, 1)), col=4)
# ベクトル図
m <- max(abs(c(a, b))) # ベクトル図のスケールを決める
lim <- m * c(-1.2, 1.2)
par.org <- par(pty="s") # 正方形のグラフを描く
plot(0, 0, type="n", xlim=lim, ylim=lim,
xlab="x", ylab="y") # スケールの設定のみ
abline(h=0) # 水平線
abline(v=0) # 垂直線
arrow(0, 0, a, 0, col=2) # 正弦波のベクトル表示
text(a, -0.1*m, format(signif(a, 3)), col=2)
arrow(0, 0, 0, b, col=3) # 余弦波のベクトル表示
text(-0.1*m, b, format(signif(b, 3)), col=3, adj=1)
arrow(0, 0, a, b, col=4) # 合成波のベクトル表示
text(a*1.1, b*1.1, format(signif(Vm, 3)), col=4)
par(par.org) # グラフパラメータを元に戻す
}
このプログラムでは,いくつか標準ではない関数が使われています. この関数を使うために,メニューの ファイル
このようにして読み込まれた関数は, Rを終了するときに作業スペース(image)を保存しておけば, 次回からは自動的に使えるようになります(図22).
位相を求めるのに,atan() ではなく atan2(y, x) を使っていますが,
こちらを使うと角度を - ![]() から
から ![]() の範囲で求められます.
グラフを描くときに
の範囲で求められます.
グラフを描くときに xaxt="n" とすると,x 軸の目盛は自動で描かれません.
axis() で自分の好きなように目盛を付けられます.
abline() で,垂直線(v=)や水平線(h=),
あるいは任意の y = a + bx という直線を描くことができます.
text() で,グラフ上に文字列を描けます.
format() は,表示用に適切に丸めた文字列を返します.
ふつう,format() は複数の数値の表示桁数を揃えるのに使い,
桁数が少ない場合は,先頭に空白が付加されます.
par(pty="s") で,グラフを実際に描く領域が正方形になります.
この関数の名前を ac43 とすると,
> ac43(1.732, 1) max(z)=1.999517 Vm=1.999956 phi=30.00073
のようにして使います. 実行結果を図23に示します.
さて,この結果を使うと,式(30)を次のように書き換えることができます.
| vi | = | VRmsin( |
|
| = | 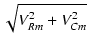 sin( sin( |
||
| = | Vimsin( |
||
| Vim | = | 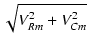 = = 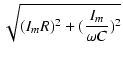 = Im = Im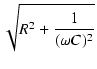 |
|
| tan |
= | - |
これを図で表すと,図24のようになります (図中の電圧は,必ずしも最大値でなくても(たとえば実効値)よいので, m を付けていません).
電流を基準にしたとき,入力電圧は ![]() だけ進んでいます.
この場合,
だけ進んでいます.
この場合,![]() の符号は負になるので,入力電圧は電流よりも位相が遅れています.
の符号は負になるので,入力電圧は電流よりも位相が遅れています.
求めたかったのは,入力と出力の関係なので,
入力電圧を基準にすると,電流は ![]() だけ遅れており(実際は
だけ遅れており(実際は ![]() が負なので進んでおり),出力の位相は電流よりも 90o 遅れます.
つまり,図24の矢印の向きは,それぞれの電圧の初期位相を表していることになります.
が負なので進んでおり),出力の位相は電流よりも 90o 遅れます.
つまり,図24の矢印の向きは,それぞれの電圧の初期位相を表していることになります.
ここで基準を入力電圧にします. つまり,Vi を右向きにします. すると図25のようになります.
この図からわかるように, 抵抗の両端の電圧は,入力電圧より|
A = |
(35) |
| A | = | ||
| = | 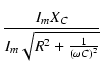 |
||
| = | 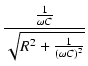 |
(36) | |
| = | tan-1 |
||
| = | tan-1 |
||
| = | tan-1 |
||
| = | tan-1( |
(37) |
Z = 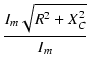 = = 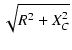
|
(38) |
この回路では,流れている電流がどこでも同じため, 各部の電圧の比率は,そのまま各部のインピーダンスの比率になります(図25の右側). つまり,回路を流れる電流を仮定しなくても, インピーダンスの比率を求め,ベクトル図を作図できます. そして,
Vo = 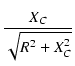 Vi Vi
|
(39) |
これで,このローパスフィルタのゲインと位相の周波数特性を描くことができます. Rで描いてみましょう.
function ()
{
R <- 15.9e3 # 抵抗値
C <- 0.01e-6 # 容量
f <- dec(10, 100e3, 30) # 周波数(対数で,10倍あたり30点ずつ)
w <- 2 * pi * f # 角周波数(omega と書くのは大変なので w を使用)
XC <- 1/(w * C) # コンデンサのリアクタンス
A <- XC / sqrt(R^2 + XC^2) # ゲイン
phi <- atan(-w * C * R) # 位相(進みが正)
par(mfrow=c(2, 1))
semilogplot(f, dB(A), type="l", col="red",
xlab="Frequency (Hz)", ylab="Gain (dB)")
semilogplot(f, phi*180/pi, type="l", col="red",
xlab="Frequency (Hz)", ylab="Phase (deg)")
}
dec(from, to, n) は,周波数などとして使う等比数列を生成する関数で,
from から to まで,10倍ごとに n 点きざみの等比数列を生成します.
semilogplot は,横軸が対数で,縦軸が通常のグラフを描く関数です.
dB(x) は,
20 log10(x) を返す関数です.
振幅が V1 初期位相が ![]() の正弦波 v1 と,
振幅が V2 初期位相が
の正弦波 v1 と,
振幅が V2 初期位相が ![]() の正弦波 v2 を加えた結果を v3 とします.
この v3 の振幅 V3 と初期位相
の正弦波 v2 を加えた結果を v3 とします.
この v3 の振幅 V3 と初期位相 ![]() を求めます.
を求めます.
| v1 | = | V1sin( |
(40) |
| v2 | = | V2sin( |
(41) |
| v3 | = | V3sin( |
(42) |
| v3 | = | V1sin( |
|
| = | V1cos |
||
| + V2cos |
|||
| = | (V1cos |
(43) |
|
v3 = V3sin( |
(44) |
| V3cos |
= | V1cos |
(45) |
| V3sin |
= | V1sin |
(46) |
具体的に振幅と位相を求めると,図より,
先に進む前に,ここで示したベクトルによる計算をいくつかやってみましょう.
この回路の場合,各素子にかかっている電圧は,すべて等しく v ですので, この位相を基準にします. 抵抗を流れる電流 iR の位相は電圧の位相と同じで,大きさは,
|
IR = |
(49) |
XC = 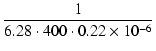 = 1810 [Ω] = 1810 [Ω]
|
(50) |
|
IC = |
(51) |
流れる電流の大きさ I は,
I = 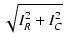 = = |
(52) |
|
|
(53) |
図29は,負帰還の微分補償で使われる回路です. R1 は帰還抵抗で,これに並列に C を入れることにより, 高域の負帰還量が増えます. この回路の入力(アンプの出力)と出力(アンプの入力部に帰還される信号)の関係を調べましょう. あらかじめ断っておきますが,この解析は大変複雑になります. ベクトル図による方法は,この程度の回路で,もはや使い物にならないことがわかるでしょう.
この回路は複雑なので,部分部分に分けて解析していきます. まず,R1 の両端の電圧を v1 として,R1 と C の並列接続に注目します. v1 の位相を基準とすると,R1 を流れる電流 iR1 の位相は v1 と同じです. コンデンサを流れる電流の位相は v1 より 90o 進んでいます. したがってベクトル図は,図30の左のようになります.
ここまでの関係から,
| XC | = | ||
| IC | = | ||
| IR1 | = | ||
| I | = | 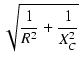 |
出力 vo は,i が R2 を流れて生じる電圧なので,
その位相は i と同じで,v1 よりも ![]() 進んでいます.
入力電圧 vi は,v1 と vo を加えた物ですから,
そのベクトル図は,図30の右のようになります.
出力の位相は,入力よりも
(
進んでいます.
入力電圧 vi は,v1 と vo を加えた物ですから,
そのベクトル図は,図30の右のようになります.
出力の位相は,入力よりも
(![]() -
- ![]() ) だけ進んでいます.
) だけ進んでいます.
ゲインを求めてみましょう.
式(54)より,
| Vo | = | V1R2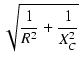 |
|
| V1 | = | 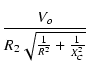 |
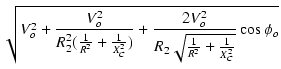
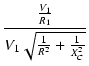 =
=